一、引言
分布类可视化图像是一类用于直观展示数据分布特征的图形,通过图形化的方式呈现数据在不同取值范围内的分布情况、集中趋势、离散程度等信息,帮助人们更快速、准确地理解数据的内在规律和特征。
二、几类分布类可视化图像介绍
(1)直方图(Histogram)
特点:将数据分组,用长方形的高度来表示落在各个组内的数据频数,展示数据的分布形状、中心位置和离散程度等。直方图的 x 轴表示数据的取值区间,y 轴表示频数或频率。但分组的选择对结果影响较大,不同的分组方式可能会呈现出不同的数据分布形态,而且无法直接反映数据的具体数值。同时,还可以变换为加权直方图和百分比直方图等形式。
加权直方图:普通直方图中每个数据点的权重是相等的,而加权直方图允许为每个数据点赋予不同的权重。
百分比直方图:将直方图的纵坐标由频数改为频率(即每个区间的频数占总频数的百分比),这样可以更方便地比较不同数据集的分布形状,而不受数据总量的影响。
应用场景:常用于展示连续型数据的分布情况,例如学生成绩分布、人口年龄分布等。
Python 实现(以 matplotlib 为例):
import numpy as np
import matplotlib.pyplot as plt
# 设置中文显示和全局样式
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.style.use('ggplot') # 使用更清晰的ggplot风格
# 生成非对称数据(增加偏态差异)
data = np.concatenate([
np.random.normal(-2, 1, 300),
np.random.normal(3, 0.5, 700)
])
# ----------------------------
# 图1:普通直方图 vs 百分比直方图
# ----------------------------
plt.figure(figsize=(10, 4))
# 普通直方图(频数统计,分箱较宽)
plt.subplot(1, 2, 1)
counts, bins, _ = plt.hist(
data, bins=15, color='skyblue', edgecolor='black', alpha=0.8
)
plt.xlabel('数值区间')
plt.ylabel('频数')
plt.title('普通直方图(分箱数=15)')
plt.annotate(f'总样本数: {len(data)}',
xy=(0.65, 0.9), xycoords='axes fraction',
bbox=dict(boxstyle="round", fc="white"))
# 百分比直方图(密度归一化,分箱更细)
plt.subplot(1, 2, 2)
plt.hist(
data, bins=30, density=True,
color='salmon', edgecolor='black', alpha=0.8
)
plt.xlabel('数值区间')
plt.ylabel('概率密度')
plt.title('百分比直方图(分箱数=30)')
plt.annotate('总面积=1',
xy=(0.65, 0.9), xycoords='axes fraction',
bbox=dict(boxstyle="round", fc="white"))
plt.tight_layout()
plt.show()
# ----------------------------
# 图2:加权直方图(设计明显权重差异)
# ----------------------------
# 生成权重:对数值>0的点赋予更高权重
weights = np.where(data > 0, 3.0, 0.5) # 右侧权重是左侧的6倍
plt.figure(figsize=(8, 4))
plt.hist(
data, bins=20, weights=weights,
color='green', edgecolor='black', alpha=0.8
)
plt.xlabel('数值区间')
plt.ylabel('加权频数')
plt.title('加权直方图(右侧权重×6)')
plt.annotate('权重策略:\n>0 → 3.0\n≤0 → 0.5',
xy=(0.65, 0.8), xycoords='axes fraction',
bbox=dict(boxstyle="round", fc="white"))
plt.show()
结果展示:

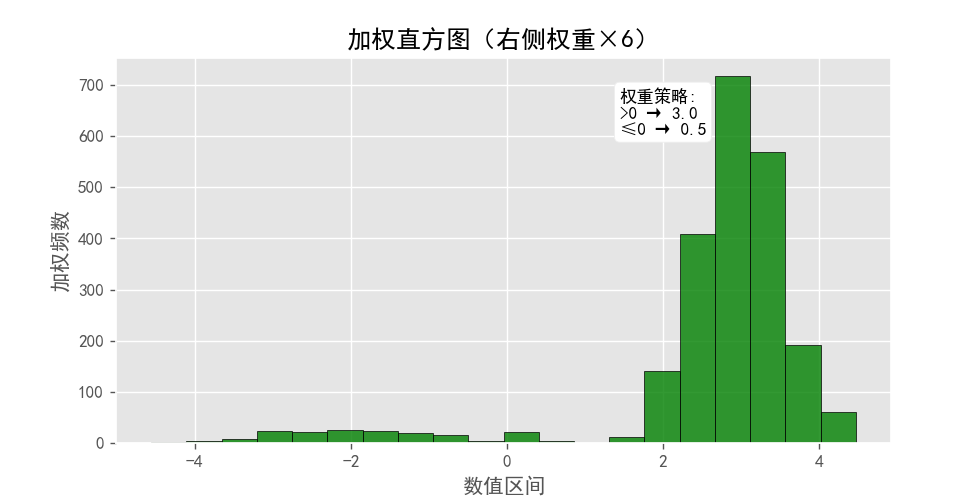
结果分析:
1.普通直方图(频数统计)
数据为双峰分布,左侧峰值在 -2 附近(样本量约300),右侧峰值在 3 附近(样本量约700)。右峰因样本量更大(700 vs 300),柱状条高度显著高于左峰。使用 15个分箱,粗粒度分箱合并细节,突出双峰主结构。各分箱宽度为 (max - min) / 15 ≈ 0.73,区间划分较宽。
直观显示数据分布的主形态(双峰偏态),Y轴为实际频数,右峰高度反映样本量优势。
2. 百分比直方图(密度归一化)
同一组数据,但通过 density=True 将频数转换为 概率密度,使得总面积等于1。右峰因样本量更多,其密度值更高(右侧样本占比70%)。使用 30个分箱,细粒度分箱捕捉更多分布细节。分箱宽度为 (max - min) / 30 ≈ 0.37,区间划分更精细。Y轴为概率密度,右峰密度值更高(约0.3 vs 左峰0.1),反映右侧数据集中程度更高。分箱细化后,可观察到右侧分布更集中(标准差0.5),左侧更分散(标准差1)。
3. 加权直方图(权重设计)
对 数值 > 0 的点赋予 3倍权重,其他点赋予 0.5倍权重。权重显著放大右侧数据的影响,抑制左侧数据。使用 20个分箱,平衡权重调整后的分布形态。
右峰加权频数急剧升高,左峰几乎被压制(权重×0.5)。人工干预分布权重,模拟实际场景(如对高价值样本的强调)。
(2)密度图(Density Plot)
特点:通过核密度估计(KDE)来展示数据的概率密度函数,平滑地描绘出数据的分布形态,相比直方图更能体现数据的分布趋势。然而,核密度估计的方法和参数选择会影响曲线的平滑程度,可能会过度平滑或保留过多噪声,导致对数据分布的误判;对于小样本数据,密度图的准确性较差。此外,还可变换为和分组密度图。
分组密度图:按照某个分类变量将数据分组,然后分别绘制每组数据的密度图。
应用场景:同样适用于连续型数据,用于比较不同数据集的分布,或者观察单个数据集的分布特征,如判断数据是否符合某种分布(正态分布、偏态分布等)。
Python 实现(以 seaborn 为例):
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 对于 Windows 系统
plt.rcParams['axes.unicode_minus'] = False
# 生成随机数据
data = np.random.normal(0, 1, 1000)
# 普通密度图
plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
sns.kdeplot(data, fill=True)
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Normal Density Plot Example')
# 分组密度图示例
category = np.random.choice(['A', 'B'], size=len(data)) # 生成随机分类数据
data_A = data[category == 'A']
data_B = data[category == 'B']
plt.subplot(1, 2, 2)
sns.kdeplot(data_A, fill=True, label='A')
sns.kdeplot(data_B, fill=True, label='B')
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Grouped Density Plot Example')
plt.legend()
plt.tight_layout()
plt.show()
结果展示

左侧:Normal Density Plot Example(普通密度图示例)
- 数据分布特征:
- 曲线呈现出单峰形态,说明数据集中大部分数据集中在某个特定值附近 ,在该例中峰值大概位于0附近,意味着数据的中心位置在0左右。
- 曲线左右两侧近似对称,表明数据的分布具有近似正态分布的特征 ,即数据围绕均值呈现出钟形对称分布,两侧数据逐渐减少。
- 曲线在纵轴(Density)上的取值范围表明了数据在不同位置的相对密度大小,在峰值处密度最大,随着向两侧延伸,密度逐渐趋近于0 。
右侧:Grouped Density Plot Example(分组密度图示例)
- 数据分布特征:
- 整体趋势:两组数据(A和B)都呈现出单峰的分布形态,且峰值都大致在0附近,说明两组数据的中心位置相近,大部分数据都集中在0值附近 。
(3)箱线图(Box Plot)
特点:通过绘制数据的四分位数(包括最小值、第一四分位数 Q1、中位数、第三四分位数 Q3 和最大值),展示数据的分布范围、中位数位置、数据的离散程度以及是否存在异常值。箱线图中间的箱体表示 Q1 到 Q3 的范围,箱体中间的横线为中位数,箱体上下的 whiskers 分别表示数据的最小值和最大值(不包括异常值),异常值通常用单独的点表示。但它只能展示数据的一些统计量,无法展示数据的具体分布形状,对于分布较为复杂的数据,可能无法提供足够的信息。同时,还可以变换为水平箱线图和美化箱线图等。
水平箱线图:将传统垂直方向的箱线图改为水平方向展示,当变量名称较长时,水平箱线图能更方便地标注变量名称,使图表更易读。
应用场景:可用于比较不同数据集的分布特征,检测数据中的异常值,以及了解数据的偏态和尾重情况。例如比较不同班级学生成绩的分布。
Python 实现(以 matplotlib 为例):
import numpy as np
import matplotlib.pyplot as plt
# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 对于 Windows 系统
plt.rcParams['axes.unicode_minus'] = False
# 生成随机数据
data = np.random.normal(0, 1, 1000)
# 普通箱线图
plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.boxplot(data)
plt.ylabel('Value')
plt.title('Normal Box Plot Example')
# 水平箱线图
plt.subplot(1, 2, 2)
plt.boxplot(data, vert=False)
plt.xlabel('Value')
plt.title('Horizontal Box Plot Example')
plt.tight_layout()
plt.show()
结果展示

结果分析:
左侧:Normal Box Plot Example(普通箱线图示例)
1.箱体
箱体中间的橙色横线代表中位数,从图中可看出中位数约为 0 ,这表明数据集中有一半的数据小于或等于 0,另一半大于或等于 0 。
箱体的上下边界分别是第一四分位数(Q1)和第三四分位数(Q3)。这意味着约 50% 的数据落在 Q1 和 Q3 之间,反映了数据的中间分布范围 。通过箱体的长度,可以初步判断数据在中间部分的离散程度,箱体越短,说明这部分数据越集中。
2.须(whiskers)
从箱体向上和向下延伸的直线(须),代表数据的取值范围(不包含异常值) 。须的端点表示数据中除异常值外的最小值和最大值。图中须的长度表明数据在中位数两侧有一定的波动范围。
3.异常值
图中箱体上方和下方的圆圈代表异常值。异常值是指那些明显偏离数据主体的观测值 ,它们可能是由于数据录入错误、测量误差或真实存在的极端值等原因造成的。箱体上方有多个异常值,说明在数据的较大取值方向上存在一些极端的观测点。
右侧:Horizontal Box Plot Example(水平箱线图示例)
水平箱线图与普通箱线图展示的信息本质相同,只是方向改变为水平方向。
1.箱体
橙色竖线代表中位数,同样约为 0 ,体现数据的中间位置。
箱体左右边界为 Q1 和 Q3,显示数据中间 50% 的分布区间 ,从箱体宽度可判断数据在中间部分的离散程度。
2.须(whiskers)
水平延伸的直线(须)表示非异常值的数据范围,左右端点分别为非异常值的最小值和最大值 ,反映数据在中位数两侧的波动情况。
3.异常值
图中左右两侧的圆圈为异常值,左侧有一个异常值,右侧有多个异常值,表明在数据的较小和较大取值方向上均存在极端观测点 。
(4)小提琴图(Violin Plot)
特点:结合了箱线图和密度图的特点,中间的白色部分是箱线图的箱体,展示数据的四分位数,两侧的曲线是数据的密度曲线,反映数据在不同位置的分布密度。小提琴图既可以展示数据的分布形状,又能体现数据的离散程度和集中趋势。但当数据集数量较多时,图表可能会显得过于复杂,难以解读;而且小提琴图的形状可能会受到数据集中极端值的影响。此外,还可变换为嵌套小提琴图。
嵌套小提琴图:当有多个层次的分类变量时,可以绘制嵌套小提琴图。先按照一个分类变量分组,然后在每个组内再按照另一个分类变量进一步细分,绘制嵌套的小提琴图,便于深入分析不同层次变量对数据分布的影响。
应用场景:常用于比较多个数据集的分布,例如比较不同地区的收入分布,或者同一变量在不同时间点的分布变化。
Python 实现(以 seaborn 为例):
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
# 设置中文和字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 生成差异化数据(关键修改点)
np.random.seed(42) # 固定随机种子保证可复现
# ------------------------------------------------------------
# 图1:普通小提琴图(左偏态数据)
# ------------------------------------------------------------
data_left_skew = np.concatenate([
np.random.chisquare(3, 800), # 左偏态数据
np.random.normal(12, 2, 200) # 添加右尾
])
# ------------------------------------------------------------
# 图2:嵌套小提琴图(多分组对比数据)
# ------------------------------------------------------------
# 生成差异明显的分组数据
group1 = np.random.choice(['实验组', '对照组'], size=1000)
subgroup = np.random.choice(['策略A', '策略B'], size=1000)
# 为不同组合创建不同分布
data_nested = np.where(
(group1 == '实验组') & (subgroup == '策略A'),
np.random.normal(8, 1.5, 1000),
np.where(
(group1 == '实验组') & (subgroup == '策略B'),
np.random.gamma(4, 1, 1000),
np.random.uniform(-2, 2, 1000)
)
)
# 图1
plt.figure(figsize=(10, 5))
# 图1:左偏态普通小提琴图(带宽调小突出细节)
plt.subplot(1, 2, 1)
sns.violinplot(y=data_left_skew,
bw=0.3, # 减小带宽显示更多细节
inner="quartile",
color="skyblue")
plt.ylabel('数值分布')
plt.title('左偏态分布(带宽=0.3)')
# 图2:嵌套分组对比图
plt.figure(figsize=(8, 5))
sns.violinplot(x=group1,
y=data_nested,
hue=subgroup,
split=True, # 左右分裂显示子组
palette="husl", # 高对比度配色
inner="box", # 显示箱线
scale="count", # 宽度反映样本量
bw=0.4)
plt.xlabel('实验分组')
plt.ylabel('效果指标')
plt.title('分组策略对比(实验组 vs 对照组)')
plt.legend(title='子策略')
plt.grid(axis='y', linestyle='--', alpha=0.5)
plt.show()


结果分析:
左偏态分布(带宽 = 0.3)图
**图表类型与含义:**小提琴图,展示了数据的分布情况。结合了箱线图和密度图的特点,既能显示数据的集中趋势、离散程度,又能呈现数据的分布形状 。图中标题表明数据呈现左偏态分布,带宽参数为 0.3 ,带宽会影响核密度估计的平滑程度,0.3 的带宽值决定了当前图形的平滑形态。
数据分布特征:
集中趋势:从图形最宽处可大致判断数据的集中区域 ,此处表示数据出现频率较高的取值范围。
离散程度:图形的宽度变化反映数据的离散程度 ,越宽说明数据在该取值附近的离散程度越大;越窄则表示数据越集中。
偏态特征:左偏态分布意味着数据的左侧(较小值方向)有较长的尾巴 ,即存在一些较小的极端值,使得数据的均值小于中位数,分布的重心偏向右侧。
分组策略对比(实验组 vs 对照组)图
**图表类型与含义:**同样是小提琴图,用于对比实验组和对照组在不同子策略(策略 A 和策略 B)下的效果指标分布情况 。通过不同颜色区分策略 A(粉红色)和策略 B(蓝绿色),并在图中嵌入了箱线图元素(黑色箱体和线条)展示关键统计量。
数据分布特征:
对照组:策略 A 和策略 B 的数据分布在效果指标上有一定重叠 ,说明两种策略在对照组中的效果有相似之处。箱线图显示了中位数和四分位数范围,可看出数据的集中趋势和中间 50% 数据的离散程度 。
实验组:策略 A 和策略 B 的数据分布差异更为明显 。策略 A 的效果指标取值整体相对较高,且分布范围较窄,说明该策略下效果指标较为集中;策略 B 的取值范围更广,离散程度较大 。对比对照组和实验组,能发现不同策略在实验前后对效果指标分布产生的影响,可用于评估策略的有效性和稳定性。
(5)Q-Q 图(Quantile-Quantile Plot)
特点:用于比较两个数据集的分布是否相似,或者判断一个数据集是否符合某种理论分布(如正态分布)。Q-Q 图通过绘制两个数据集的分位数之间的关系来展示分布的相似性,如果两个数据集分布相似,那么 Q-Q 图上的点会大致落在一条直线上。但它对理论分布的假设较为敏感,如果选择的理论分布与实际数据分布不符,可能会得出错误的结论;对于小样本数据,Q-Q 图上的点可能会有较大的波动,影响判断的准确性。此外,还可变换为分位数回归 Q-Q 图和分组 Q-Q 图等。
分位数回归 Q-Q 图:在传统 Q-Q 图的基础上,引入分位数回归的方法,通过拟合分位数之间的关系来更准确地评估数据与理论分布的一致性,尤其适用于数据存在异方差性或非正态分布的情况。
应用场景:在数据分析和统计建模中,常用于检验数据是否满足某些假设条件,例如在回归分析中检验残差是否服从正态分布。
Python 实现(以 statsmodels 库为例):
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
from statsmodels.graphics.gofplots import qqplot
# 设置中文和字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 生成非正态数据(右偏态)
np.random.seed(42)
data = np.random.chisquare(3, 500) # 卡方分布(自由度=3)
# 绘制基础Q-Q图(对比正态分布)
plt.figure(figsize=(8, 4))
stats.probplot(data, dist="norm", plot=plt)
plt.plot([-2, 5], [-2, 5], 'r--', linewidth=1, label='理论正态分布') # 添加参考线
plt.title('基础Q-Q图(右偏态数据 vs 正态分布)')
plt.legend()
plt.grid(linestyle='--', alpha=0.5)
plt.show()
结果展示

结果分析:
这张基础Q - Q图用于比较右偏态数据与理论正态分布,横轴是理论正态分布分位数,纵轴是右偏态数据排序后的取值。红色虚线为理论正态分布参考线,红色实线是拟合趋势线,蓝色圆点代表数据对应关系。图中显示,数据中间部分与正态分布相似,两端差异明显,左侧数据点在参考线下方,右侧在上方,体现右偏态数据存在较大极端值、分布向右偏斜的特征,表明该右偏态数据与理论正态分布有差异。
三、总结
本次实验聚焦分布类可视化图像,旨在理解其特性、应用场景并掌握用Python实现的方法。实验中利用多种Python库分别生成了直方图、密度图、箱线图、小提琴图和Q-Q图及其变换形式。如通过改变直方图的分箱数和权重、密度图的分组、箱线图的方向、小提琴图的嵌套以及Q-Q图的对比分布等,展示了不同图表对数据分布的呈现效果。结果表明,各类图表各有优劣和适用场景,数据预处理会影响图表展示,多种图表综合运用能更全面剖析数据,这为后续数据分析工作筑牢了基础。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








