Python学习：面向对象编程应用实例1——简支梁强度校核

已于 2025-03-29 20:43:35 修改
阅读量979 收藏 27
点赞数 30
文章标签： 学习
于 2025-03-29 20:41:24 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_74999972/article/details/146709314
版权

一、问题阐述

        已知将动车制动系统上某一杠杆简化为简支梁，其材料为铸钢，其屈服强度为230Mpa，许用应力为138Mpa。截面是一个高10mm，宽20mm的矩形，总长度为221.5mm，受力情况如下

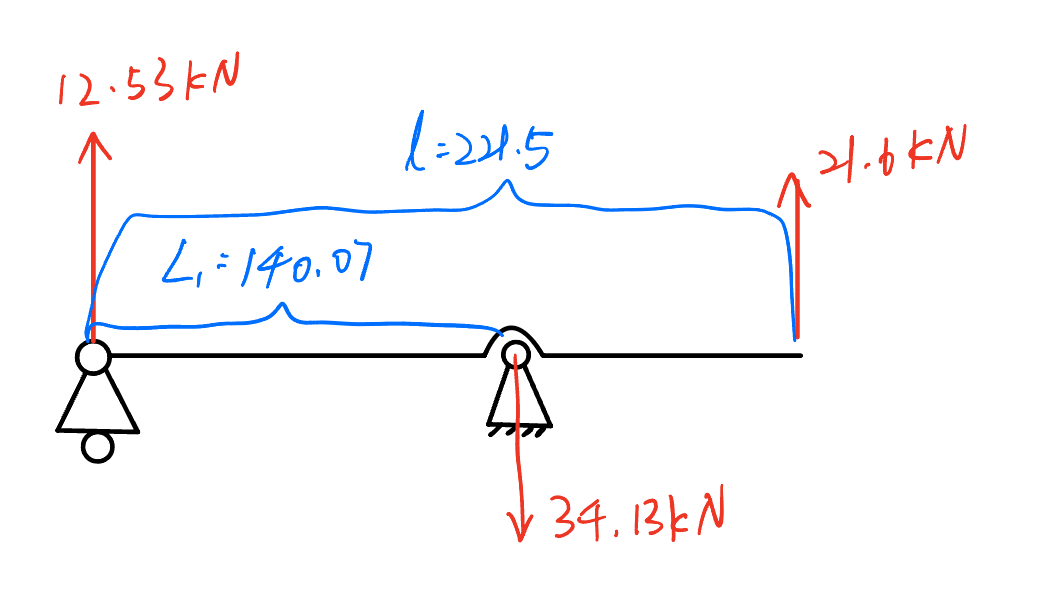
对该简支梁进行强度校核，并绘制剪力图和弯矩图

二、编程思路

想象你是一名工程师，需要对一根简支梁进行强度校核。你需要准备哪些信息？

  1. ​材料属性：梁是用什么材料做的？钢材还是铝材？强度如何？
  2. ​几何尺寸：梁是什么形状的？矩形还是圆形？尺寸多大？
  3. ​受载情况：梁承受了什么样的力？集中力还是分布力？作用在哪里？

        三部分信息天然地符合了面向对象编程中的什么时候定义类的思想，我们自然地将这三部分定义为三大类：MaterialAttribute（材料属性），GeometricDimension（几何尺寸）以及LoadCurve（受载情况）。

        然后我们创建一个"执行器"类，专门负责强度校核计算，将这套方法也定义成一个类BeanIntensityCheck（梁的强度校核）。这个BeanIntensityCheck就像一台"强度校核机器"，你只需要把三大信息（材料、尺寸、载荷）输入进去，它就能自动完成所有计算和绘图工作。

        这样，我们就明确要定义三大信息类以及一大执行器类

        在面向对象编程（OOP）中，​定义类时主要关注两个核心部分：1、类的属性（数据）2、​实例方法（行为）。所以接下来确定我们所定义的四大类中的属性和方法

（1）MaterialAttribute类（材料属性）

        在强度校核中，我们提供被校核的梁的材料，其屈服强度，许用应力，弹性模量等材料属性（本例中只需要许用应力），因此我们传递这些信息进入该类中。我们不需要对这些属性进行操作，所以不需要编写对应的实例方法，所以我们在python中定义该类如下

# 定义材料属性
class MaterialAttribute(object):
    def __init__(self, name , yield_strength , permissible_stress):
        self.name = name # 材料名称
        self.yield_strength = yield_strength # 材料的屈服强度
        self.Permissible_Stress = permissible_stress # 材料的许用应力

结合本题要求，我们可以定义该简支梁材料作为本类的一个实例对象，如下操作

Lever_Bean_Material = MaterialAttribute('铸钢',230,138)

（2）GeometricDimension类（几何尺寸）

        在强度校核中，我们提供被校核的梁的长度与截面信息。梁的截面例如经典的圆形截面梁，矩形截面梁或工字截面等，不同的截面有不同的截面几何尺寸，因此我们需要一个分类器来判断我们提供的截面是什么形状的。

        在确定截面形状后，我们需要根据截面几何尺寸计算最重要的一个属性——抗弯截面系数W，因此我们需要在传入截面信息后计算出W这个参数。至于实例方法我们也不需要定义，所以我们在python中定义该类如下

# 定义几何尺寸
class GeometricDimension(object):
    def __init__(self, shape:str , length , **sectional_dimension): #sectional_dimension传递的是截面尺寸信息
        self.shape = shape
        self.length = length
        self.sectional_dimension = sectional_dimension
        # 矩形截面
        if shape == '矩形':
            # __init__rectangle是一个实例方法，由实例对象调用，因此调用时要加self.
            self.__init_rectangle(**sectional_dimension)
        # 圆形截面
        elif shape == '圆形':
            self.__init_circle(**sectional_dimension)
        # 其它截面计算暂时未开发
        else:
            pass

例如本题的简支梁截面是一个高10mm，宽20mm的矩形，总长度为221.5mm，所以我们可以定义该简支梁形状作为本类的一个实例对象，如下操作

Lever_Bean_Geometry = GeometricDimension('矩形',221.5, width = 20,height = 10)

（3）LoadCurve类（受载情况）

        同上两种情况，我们在python中定义该类如下

# 定义受弯载荷情况
class LoadCurve(object):
    def __init__(self,type_define:str,loads_type:str,**force_analysis):
        self.type_define = type_define
        self.loads_type = loads_type
        self.force_analysis = force_analysis
        if type_define == '单一载荷情况':
            if loads_type == '集中力':
                self.__init_force(**force_analysis)

            elif loads_type == '均布载荷':
                self.__init_pressure(**force_analysis)

            else:
                pass
        else:
            pass

    # 初始化集中力分布
    def __init_force(self,force_value=None,position=None):
        """
        定义从左往右集中力的大小和位置
        :param force_value: 集中力值列表，例如 [100, 200] 表示两个力
        :param position: 集中力位置列表，例如 [0.5, 1.0] 表示在0.5mm和1.0mm处
        """
        self.force_value =np.array(force_value) if force_value is not None else []
        self.position = np.array(position) if position is not None else []

        # 验证输入结果
        if len(self.force_value) != len(self.position):
            print("提供的力的数量和位置的数量不相同")
            self.force_value = None
            self.position = None

    # 初始化均布载荷分布
    def __init_pressure(self,**force_analysis):
        pass

结合本题要求，我们可以定义该简支梁受载情况作为本类的一个实例对象，如下操作

Lever_Bean_Load = LoadCurve('单一载荷情况','集中力',force_value=[12.53,-34.13,21.6], position = [0,140.07,221.5])

（4）BeanIntensityCheck类（强度校核执行器）

       当我们需要将材料所有属性提供给执行器，我们就可以通过执行器来对我们的梁强度进行校核，三大信息类与一大执行器类的关系我们可以如此描绘

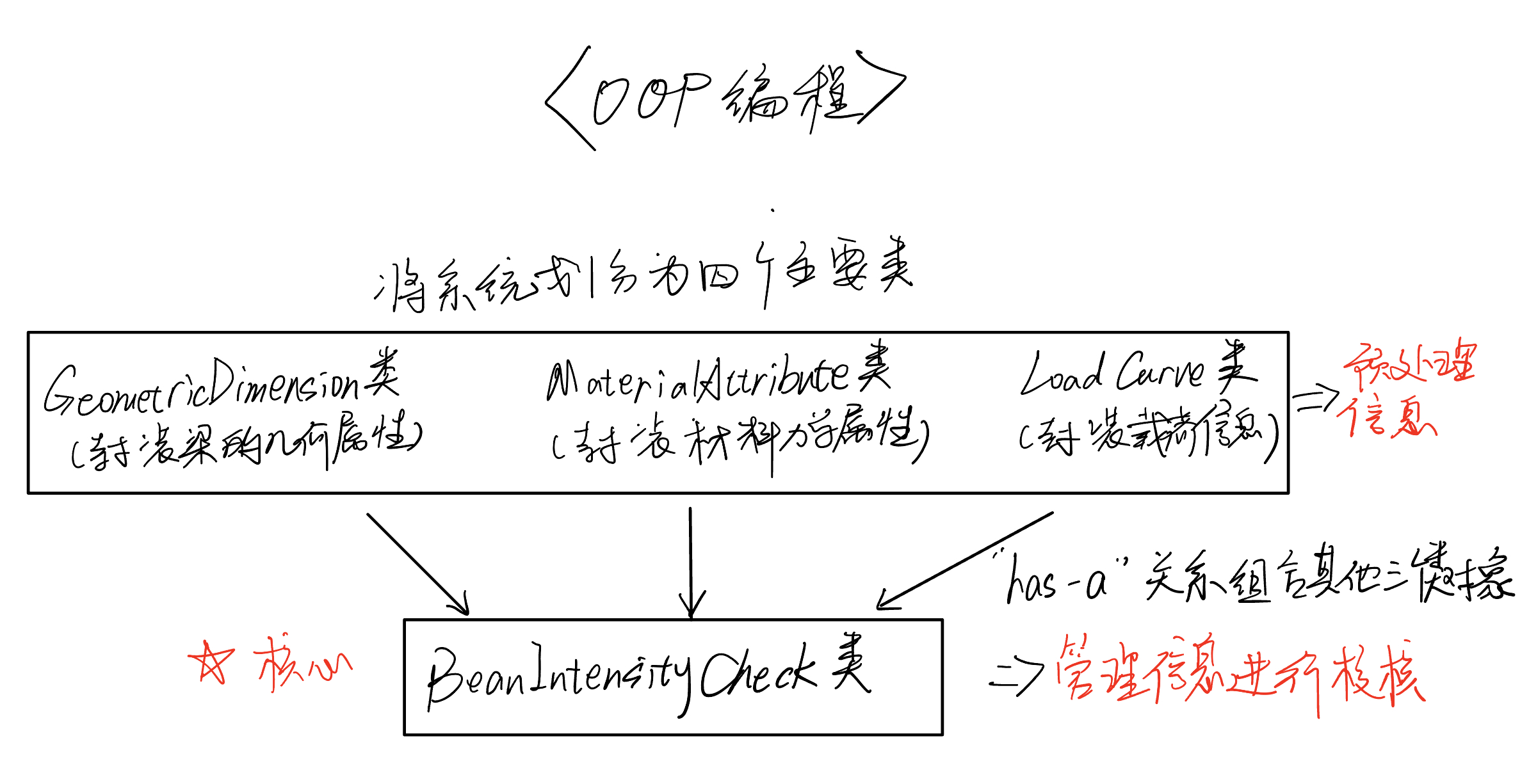
        所以我们可以如此初始化该类

#梁的强度校核
class BeanIntensityCheck(object):

    # 初始化
    def __init__(self,material:MaterialAttribute,geometry:GeometricDimension,load:LoadCurve):
        self.material = material
        self.geometry = geometry
        self.load = load

        如此操作后，我们便可以在执行器中调用提供的所有信息。为了检查我们提供的信息是否正确，我们可以写一个函数来打印我们传递的信息，因为我们需要定义一个具体的对象来传递这些信息，所以显然这个函数在类中便是一个实例方法，我们定义其为show(self)

# 显示梁的信息
    def show(self):
        print('梁的材料信息：材料种类——{}，屈服强度——{}Mpa，许用应力——{}Mpa'.format(self.material.name,self.material.yield_strength,self.material.Permissible_Stress))
        print('梁的几何信息：截面形状——{}，长度——{}mm，截面模量——{:.2f}Mpa'.format(self.geometry.shape,self.geometry.length,self.geometry.section_modulus))
        print('梁的加载信息：加载力的类型是{}，其大小为{}(kN)，其所在位置为{}(mm)'.format(self.load.loads_type,self.load.force_value,self.load.position))

        接下来便是结合所有的信息对梁进行校核了，在这里我们就需要添加对应的实例方法——intensity_check()（强度校核）。

    # 计算最大弯矩
    def max_bending_moment(self):
        slope = np.cumsum(np.array([self.load.force_value[0], self.load.force_value[1]]))
        x = np.linspace(self.load.position[0], self.load.position[-1], 1000)
        y = np.zeros_like(x)

        # 第一段：x <= position[1]
        mask1 = x <= self.load.position[1]
        y[mask1] = slope[0] * x[mask1]

        # 第二段：x > position[1]
        mask2 = x > self.load.position[1]
        y[mask2] = slope[0] * self.load.position[1] + slope[1] * (x[mask2] - self.load.position[1])

        return max(y)

   # 强度校核
    def intensity_check(self):
        M_max = self.max_bending_moment()
        sigma = M_max / self.geometry.section_modulus
        if sigma < self.material.Permissible_Stress:
            print('计算出的弯曲应力大小为 {:.2f} Mpa，小于许用应力 {} Mpa，故符合强度要求'.format(sigma,self.material.Permissible_Stress))
        else:
            print('计算出的弯曲应力大小为 {:.2f} Mpa，大于许用应力 {} Mpa，不符合强度要求，请重新设计'.format(sigma,self.material.Permissible_Stress))

        在校核后，我们希望绘制剪力图与弯矩图，同样给出对应的实例方法如下

    # 绘制剪力图——阶梯图 (小金鱼跑的)
    def plot_shear_diagram(self):
        position = self.load.position
        shear_forces = self.load.force_value[0:2]
        new_shear_forces = np.append(shear_forces, 0)  # 终点位置剪力应为0
        x = [0] + position  # 添加起点
        y = [0] + new_shear_forces  # 添加起点剪力值

        plt.rcParams['font.sans-serif'] = ['SimHei']
        plt.rcParams['axes.unicode_minus'] = False
        fig, ax = plt.subplots(figsize=(16, 9))

        # 绘制阶梯图
        ax.step(x, y, where='post', color='b', linewidth=1.5, label='剪力')

        # 填充灰色阴影
        ax.fill_between(x, y, 0, step='post', color='gray', alpha=0.3)

        # 在剪力转折点标注剪力值（增大字体到12pt）
        for i in range(len(x)):
            label = f"{y[i]:.1f} kN"
            offset_x = 0.02 * max(x)  # x方向偏移
            offset_y = 0.05 * max(abs(np.array(y)))  # y方向偏移

            ax.text(
                x[i] + offset_x,
                y[i] + offset_y,
                label,
                ha='left',
                va='bottom',
                fontsize=12,  # 关键修改：增大字体到12pt
                bbox=dict(facecolor='white', edgecolor='none', alpha=0.8)
            )

        # 设置带箭头的坐标轴
        ax.spines['right'].set_visible(False)
        ax.spines['top'].set_visible(False)
        ax.spines['left'].set_position(('data', 0))
        ax.spines['bottom'].set_position(('data', 0))

        # 添加坐标轴箭头
        ax.plot(1, 0, ">k", transform=ax.get_yaxis_transform(), clip_on=False, markersize=10)
        ax.plot(0, 1, "^k", transform=ax.get_xaxis_transform(), clip_on=False, markersize=10)

        # 坐标轴标签也增大字体（14pt）
        ax.text(1.05, 0.02, '位置 (mm)', transform=ax.get_yaxis_transform(),
                ha='left', va='center', fontsize=14)  # 增大到14pt
        ax.text(0.02, 1.05, '剪力 (kN)', transform=ax.get_xaxis_transform(),
                ha='left', va='center', fontsize=14)  # 增大到14pt

        # 标题和全局字体设置
        ax.set_title('剪力图', fontsize=16)  # 标题更大（16pt）
        ax.grid(True, linestyle='--', alpha=0.7)

        # 调整坐标轴范围
        ax.set_xlim(min(x) - 0.1 * max(x), max(x) * 1.1)
        ax.set_ylim(min(y) - 0.1 * max(abs(np.array(y))), max(y) * 1.1)

        plt.show()

    # 绘制弯矩图 (小金鱼跑的)
    def plot_bending_moment_diagram(self):
        slope = np.cumsum(np.array([self.load.force_value[0], self.load.force_value[1]]))
        x = np.linspace(self.load.position[0], self.load.position[-1], 1000)
        y = np.zeros_like(x)

        # 第一段：x <= position[1]
        mask1 = x <= self.load.position[1]
        y[mask1] = slope[0] * x[mask1]

        # 第二段：x > position[1]
        mask2 = x > self.load.position[1]
        y[mask2] = slope[0] * self.load.position[1] + slope[1] * (x[mask2] - self.load.position[1])

        # 设置中文字体和负号显示
        plt.rcParams['font.sans-serif'] = ['SimHei']
        plt.rcParams['axes.unicode_minus'] = False
        fig, ax = plt.subplots(figsize=(16, 9))

        # 绘制弯矩图
        ax.plot(x, y, 'r-', linewidth=1.5, label='弯矩')

        # 填充灰色阴影
        ax.fill_between(x, y, 0, color='gray', alpha=0.3)

        # 在关键点标注弯矩值
        key_points = [self.load.position[0], self.load.position[1], self.load.position[-1]]
        for point in key_points:
            # 计算对应的y值
            if point <= self.load.position[1]:
                y_val = slope[0] * point
            else:
                y_val = slope[0] * self.load.position[1] + slope[1] * (point - self.load.position[1])

            label = f"{y_val:.1f} kN·mm"
            offset_x = 0.02 * max(x)  # x方向偏移
            offset_y = 0.05 * max(abs(y))  # y方向偏移

            ax.text(
                point + offset_x,
                y_val + offset_y,
                label,
                ha='left',
                va='bottom',
                fontsize=12,
                bbox=dict(facecolor='white', edgecolor='none', alpha=0.8)
            )

        # 设置带箭头的坐标轴
        ax.spines['right'].set_visible(False)
        ax.spines['top'].set_visible(False)
        ax.spines['left'].set_position(('data', 0))
        ax.spines['bottom'].set_position(('data', 0))

        # 添加坐标轴箭头
        ax.plot(1, 0, ">k", transform=ax.get_yaxis_transform(), clip_on=False, markersize=10)
        ax.plot(0, 1, "^k", transform=ax.get_xaxis_transform(), clip_on=False, markersize=10)

        # 坐标轴标签
        ax.text(1.05, 0.02, '位置 (mm)', transform=ax.get_yaxis_transform(),
                ha='left', va='center', fontsize=14)
        ax.text(0.02, 1.05, '弯矩 (kN·mm)', transform=ax.get_xaxis_transform(),
                ha='left', va='center', fontsize=14)

        # 标题和全局设置
        ax.set_title('弯矩图', fontsize=16)
        ax.grid(True, linestyle='--', alpha=0.7)

        # 调整坐标轴范围
        ax.set_xlim(min(x) - 0.1 * max(x), max(x) * 1.1)
        ax.set_ylim(min(y) - 0.1 * max(abs(y)), max(y) * 1.1)

        plt.show()

        最后，我们定义该简支梁为实例对象，调用实例方法来满足题目的要求

# 添加简化为梁的实例对象 Lever
Lever_Bean = BeanIntensityCheck(Lever_Bean_Material,Lever_Bean_Geometry,Lever_Bean_Load)
Lever_Bean.show() # 显示梁的信息
Lever_Bean.plot_shear_diagram() # 绘制剪力图
Lever_Bean.plot_bending_moment_diagram() # 绘制弯矩图
Lever_Bean.intensity_check() # 强度校核

三、完整代码及结果输出

import numpy as np
import matplotlib.pyplot as plt

## 梁的强度校核
# 定义几何尺寸
class GeometricDimension(object):
    def __init__(self, shape:str , length , **sectional_dimension): #sectional_dimension传递的是截面尺寸信息
        self.shape = shape
        self.length = length
        self.sectional_dimension = sectional_dimension
        # 矩形截面
        if shape == '矩形':
            # __init__rectangle是一个实例方法，由实例对象调用，因此调用时要加self.
            self.__init_rectangle(**sectional_dimension)
        # 圆形截面
        elif shape == '圆形':
            self.__init_circle(**sectional_dimension)
        # 其它截面计算暂时未开发
        else:
            pass

    # 矩形抗弯截面强度计算
    def __init_rectangle(self,height,width):
        self.section_modulus = (width * height ** 2) / 6

    # 圆形抗弯截面强度计算
    def __init_circle(self, diameter):
        self.section_modulus = np.pi * (diameter** 3) / 32

# 定义材料属性
class MaterialAttribute(object):
    def __init__(self, name , yield_strength , permissible_stress):
        self.name = name # 材料名称
        self.yield_strength = yield_strength # 材料的屈服强度
        self.Permissible_Stress = permissible_stress # 材料的许用应力

# 定义受弯载荷情况
class LoadCurve(object):
    def __init__(self,type_define:str,loads_type:str,**force_analysis):
        self.type_define = type_define
        self.loads_type = loads_type
        self.force_analysis = force_analysis
        if type_define == '单一载荷情况':
            if loads_type == '集中力':
                self.__init_force(**force_analysis)

            elif loads_type == '均布载荷':
                self.__init_pressure(**force_analysis)

            else:
                pass
        else:
            pass

    # 初始化集中力分布
    def __init_force(self,force_value=None,position=None):
        """
        定义从左往右集中力的大小和位置
        :param force_value: 集中力值列表，例如 [100, 200] 表示两个力
        :param position: 集中力位置列表，例如 [0.5, 1.0] 表示在0.5mm和1.0mm处
        """
        self.force_value =np.array(force_value) if force_value is not None else []
        self.position = np.array(position) if position is not None else []

        # 验证输入结果
        if len(self.force_value) != len(self.position):
            print("提供的力的数量和位置的数量不相同")
            self.force_value = None
            self.position = None

    # 初始化均布载荷分布
    def __init_pressure(self,**force_analysis):
        pass

#梁的强度校核
class BeanIntensityCheck(object):

    # 初始化
    def __init__(self,material:MaterialAttribute,geometry:GeometricDimension,load:LoadCurve):
        self.material = material
        self.geometry = geometry
        self.load = load

    ## 实例方法

    # 强度校核
    def intensity_check(self):
        M_max = self.max_bending_moment()
        sigma = M_max / self.geometry.section_modulus
        if sigma < self.material.Permissible_Stress:
            print('计算出的弯曲应力大小为 {:.2f} Mpa，小于许用应力 {} Mpa，故符合强度要求'.format(sigma,self.material.Permissible_Stress))
        else:
            print('计算出的弯曲应力大小为 {:.2f} Mpa，大于许用应力 {} Mpa，不符合强度要求，请重新设计'.format(sigma,self.material.Permissible_Stress))
    # 显示梁的信息
    def show(self):
        print('梁的材料信息：材料种类——{}，屈服强度——{}Mpa，许用应力——{}Mpa'.format(self.material.name,self.material.yield_strength,self.material.Permissible_Stress))
        print('梁的几何信息：截面形状——{}，长度——{}mm，截面模量——{:.2f}Mpa'.format(self.geometry.shape,self.geometry.length,self.geometry.section_modulus))
        print('梁的加载信息：加载力的类型是{}，其大小为{}(kN)，其所在位置为{}(mm)'.format(self.load.loads_type,self.load.force_value,self.load.position))
    # 计算最大弯矩
    def max_bending_moment(self):
        slope = np.cumsum(np.array([self.load.force_value[0], self.load.force_value[1]]))
        x = np.linspace(self.load.position[0], self.load.position[-1], 1000)
        y = np.zeros_like(x)

        # 第一段：x <= position[1]
        mask1 = x <= self.load.position[1]
        y[mask1] = slope[0] * x[mask1]

        # 第二段：x > position[1]
        mask2 = x > self.load.position[1]
        y[mask2] = slope[0] * self.load.position[1] + slope[1] * (x[mask2] - self.load.position[1])

        return max(y)
    # 绘制剪力图——阶梯图 (小金鱼跑的)
    def plot_shear_diagram(self):
        position = self.load.position
        shear_forces = self.load.force_value[0:2]
        new_shear_forces = np.append(shear_forces, 0)  # 终点位置剪力应为0
        x = [0] + position  # 添加起点
        y = [0] + new_shear_forces  # 添加起点剪力值

        plt.rcParams['font.sans-serif'] = ['SimHei']
        plt.rcParams['axes.unicode_minus'] = False
        fig, ax = plt.subplots(figsize=(16, 9))

        # 绘制阶梯图
        ax.step(x, y, where='post', color='b', linewidth=1.5, label='剪力')

        # 填充灰色阴影
        ax.fill_between(x, y, 0, step='post', color='gray', alpha=0.3)

        # 在剪力转折点标注剪力值（增大字体到12pt）
        for i in range(len(x)):
            label = f"{y[i]:.1f} kN"
            offset_x = 0.02 * max(x)  # x方向偏移
            offset_y = 0.05 * max(abs(np.array(y)))  # y方向偏移

            ax.text(
                x[i] + offset_x,
                y[i] + offset_y,
                label,
                ha='left',
                va='bottom',
                fontsize=12,  # 关键修改：增大字体到12pt
                bbox=dict(facecolor='white', edgecolor='none', alpha=0.8)
            )

        # 设置带箭头的坐标轴
        ax.spines['right'].set_visible(False)
        ax.spines['top'].set_visible(False)
        ax.spines['left'].set_position(('data', 0))
        ax.spines['bottom'].set_position(('data', 0))

        # 添加坐标轴箭头
        ax.plot(1, 0, ">k", transform=ax.get_yaxis_transform(), clip_on=False, markersize=10)
        ax.plot(0, 1, "^k", transform=ax.get_xaxis_transform(), clip_on=False, markersize=10)

        # 坐标轴标签也增大字体（14pt）
        ax.text(1.05, 0.02, '位置 (mm)', transform=ax.get_yaxis_transform(),
                ha='left', va='center', fontsize=14)  # 增大到14pt
        ax.text(0.02, 1.05, '剪力 (kN)', transform=ax.get_xaxis_transform(),
                ha='left', va='center', fontsize=14)  # 增大到14pt

        # 标题和全局字体设置
        ax.set_title('剪力图', fontsize=16)  # 标题更大（16pt）
        ax.grid(True, linestyle='--', alpha=0.7)

        # 调整坐标轴范围
        ax.set_xlim(min(x) - 0.1 * max(x), max(x) * 1.1)
        ax.set_ylim(min(y) - 0.1 * max(abs(np.array(y))), max(y) * 1.1)

        plt.show()

    # 绘制弯矩图 (小金鱼跑的)
    def plot_bending_moment_diagram(self):
        slope = np.cumsum(np.array([self.load.force_value[0], self.load.force_value[1]]))
        x = np.linspace(self.load.position[0], self.load.position[-1], 1000)
        y = np.zeros_like(x)

        # 第一段：x <= position[1]
        mask1 = x <= self.load.position[1]
        y[mask1] = slope[0] * x[mask1]

        # 第二段：x > position[1]
        mask2 = x > self.load.position[1]
        y[mask2] = slope[0] * self.load.position[1] + slope[1] * (x[mask2] - self.load.position[1])

        # 设置中文字体和负号显示
        plt.rcParams['font.sans-serif'] = ['SimHei']
        plt.rcParams['axes.unicode_minus'] = False
        fig, ax = plt.subplots(figsize=(16, 9))

        # 绘制弯矩图
        ax.plot(x, y, 'r-', linewidth=1.5, label='弯矩')

        # 填充灰色阴影
        ax.fill_between(x, y, 0, color='gray', alpha=0.3)

        # 在关键点标注弯矩值
        key_points = [self.load.position[0], self.load.position[1], self.load.position[-1]]
        for point in key_points:
            # 计算对应的y值
            if point <= self.load.position[1]:
                y_val = slope[0] * point
            else:
                y_val = slope[0] * self.load.position[1] + slope[1] * (point - self.load.position[1])

            label = f"{y_val:.1f} kN·mm"
            offset_x = 0.02 * max(x)  # x方向偏移
            offset_y = 0.05 * max(abs(y))  # y方向偏移

            ax.text(
                point + offset_x,
                y_val + offset_y,
                label,
                ha='left',
                va='bottom',
                fontsize=12,
                bbox=dict(facecolor='white', edgecolor='none', alpha=0.8)
            )

        # 设置带箭头的坐标轴
        ax.spines['right'].set_visible(False)
        ax.spines['top'].set_visible(False)
        ax.spines['left'].set_position(('data', 0))
        ax.spines['bottom'].set_position(('data', 0))

        # 添加坐标轴箭头
        ax.plot(1, 0, ">k", transform=ax.get_yaxis_transform(), clip_on=False, markersize=10)
        ax.plot(0, 1, "^k", transform=ax.get_xaxis_transform(), clip_on=False, markersize=10)

        # 坐标轴标签
        ax.text(1.05, 0.02, '位置 (mm)', transform=ax.get_yaxis_transform(),
                ha='left', va='center', fontsize=14)
        ax.text(0.02, 1.05, '弯矩 (kN·mm)', transform=ax.get_xaxis_transform(),
                ha='left', va='center', fontsize=14)

        # 标题和全局设置
        ax.set_title('弯矩图', fontsize=16)
        ax.grid(True, linestyle='--', alpha=0.7)

        # 调整坐标轴范围
        ax.set_xlim(min(x) - 0.1 * max(x), max(x) * 1.1)
        ax.set_ylim(min(y) - 0.1 * max(abs(y)), max(y) * 1.1)

        plt.show()

# 添加简化为梁的实例对象 Lever
Lever_Bean_Geometry = GeometricDimension('矩形',221.5, width = 20,height = 10)
Lever_Bean_Material = MaterialAttribute('铸钢',230,138)
Lever_Bean_Load = LoadCurve('单一载荷情况','集中力',force_value=[12.53,-34.13,21.6], position = [0,140.07,221.5])
Lever_Bean = BeanIntensityCheck(Lever_Bean_Material,Lever_Bean_Geometry,Lever_Bean_Load)
Lever_Bean.show() # 显示梁的信息
Lever_Bean.plot_shear_diagram() # 绘制剪力图
Lever_Bean.plot_bending_moment_diagram() # 绘制弯矩图
Lever_Bean.intensity_check() # 强度校核

结果显示应该如下

四、结语

        代码针对本题进行设计，存在很模块化与结构化不足的地方，因此文章只作为一个简单的案例为大家提供参考~

LINOTGY0411
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值