Datawhale 数学建模导论第七章学习笔记

权重生成与评价模型

权重生成与评价模型可解决的问题：对于同一个目标，不同方案之间的比较或者是不同影响因素的比较。

权重生成与评价模型的方法：

层次分析法：

 带有一定主观性，但是好使，常常在社会科学研究中使用；用成对比较矩阵消除量纲影响。

• 层次分析法的原理：

“层次”来源于“构建层次模型图”中的“层次”，层次模型分为目标层（评价目标）、准则层（评价指标体系）、方案层（多个对比方案）。下图就是一个层次模型图：

1. 选择指标，构建层次模型：1.问题中明确给出评价指标准则，直接使用。2.问题中没有明确给出评价指标准则，需要自己查阅文献或社会调查选取指标准则。
2. 对目标层到准则层之间和准则层到方案层之间构建比较矩阵：矩阵为“正方形”即行列数相同（嘻嘻，其实就是方阵啦），，均为准则层的准则数，矩阵的每一项表示因素i和因素j的相对重要程度，矩阵具有的一些特征：

1. 对角线元素=1（因为对角线上的元素都是自己和自己做比较）
2. aij*​aji​=1

因为这个矩阵的每一项都表示因素i比因素j重要 ，为了表述重要程度，我们用1~9中间的整数描述，如下表：

如果是因素j比因素i重要，则取值应为该表中的取值的倒数。注意：由上表就可以看出来，一般对重要性的取值是奇数，当你在2个奇数之间摇摆不定，那就选这2个奇数之间的偶数。

方案层也需要构建成对比较矩阵，构建矩阵规则变了，具体如下：假如有m个准则n个样本，需要构建m个矩阵，矩阵大小为（n,n）。

     3.对每一个比较矩阵计算CR值检验是否通过CR检验，如果没有通过检验需要调整比较矩阵。

CI值：

 

RI值（随机一致性指标），通过查表可以获得，RI值表如下：

CR=CI/RI，如果CR值超过0.1，就可以认为这个矩阵是不合理，需要被修改，被调整；没有超过0.1，就可以认为这个矩阵通过了一致性检验。 

   4.求出每个矩阵最大的特征值对应的归一化权重向量：将特征向量除以该向量所有元素之和：

                                                               

 最终可以得到每个指标的权重，以及每个样本在不同指标上的归一化得分。通过加权折算就可以得到评价的最终分数。

5.根据不同矩阵的归一化权向量计算出不同方案的得分进行比较。 

• 层次分析法的案例

题目：某日从三条河流的基站处抽检水样，得到了水质的四项检测指标如下表所示。请根据提供数据对三条河流的水质进行评价。其中，DO代表水中溶解氧含量，越大越好；CODMn表示水中高锰酸盐指数，NH3-N表示氨氮含量，这两项指标越小越好；pH值没有量纲，在6~9区间内较为合适。

1.初步分析数据，确定评价指标，构建层次模型图：该评价问题共3个样本，4个评价指标 ；题目给了评价指标，构建层次模型图如下：

2.对目标层到准则层构建一个大小为4的方阵（因为准则层有4个准则） ，准则层到方案层构建4个大小为3的方阵（因为准则层有4个准则，该问题有3个样本）。例如目标层到准则层（准则层到方案层的矩阵也是这样的过程），创建如下矩阵：

对这个矩阵做特征值分析的代码如下：

import numpy as np 

# 构建矩阵
A=np.array([[1,1/5,1/3,1],
            [5,1,3,5],
            [3,1/3,1,3],
            [1,1/5,1/3,1]])

#获得指标个数
m=len(A)
n=len(A[0])
RI=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45,1.49,1.51]
#求判断矩阵的特征值和特征向量，V为特征值，D为特征向量
V,D=np.linalg.eig(A)
list1=list(V)
#求矩阵的最大特征值
B=np.max(list1)
index=list1.index(B)
C=D[:,index]

3.由上面的代码，我们可以得到最大特征值和特征向量，进而可以计算CI和CR:

CI=(B-n)/(n-1)
CR=CI/RI[n]
if CR<0.10:
    print("CI=",CI)
    print("CR=",CR)
    print("对比矩阵A通过一致性检验，各向量权重向量Q为：")
    C_sum=np.sum(C)
    Q=C/C_sum
    print(Q)
else:
    print("对比矩阵A未通过一致性检验，需对对比矩阵A重新构造")

 因为python进行矩阵分解的时候是在复数域内进行分解，所以得到的向量也是复数向量。

 计算出目标层到准则层的1个权重向量和4个准则层到方案层的权重向量以后，可以列出权重向量的排布表，如下表所示：

4. 将准则层到方案层得到的7个成对比较矩阵对应的权重向量排列为一个矩阵，矩阵的每一行表示对应的方案，矩阵的每一列代表评价准则。将这一方案权重矩阵与目标层到准则层的权重向量进行数量积，得到的分数就是最终的评分。

5.根据最终评分，得出结论：在评价过程中水中溶解氧含量与钴金属含量占评价体系比重最大，而四川攀枝花龙洞的水质虽然含钴元素比另外两个更高，但由于溶解氧更多，NH3-N的含量更小，水体不显富营养化。就整体而言，四川攀枝花龙洞得分高于重庆朱沱和湖北宜昌南津关。

将一个成对比较矩阵的AHP过程封装为函数，完整函数如下：

def AHP(A):
    m=len(A)                                     #获取指标个数
    n=len(A[0])
    RI=[0, 0, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49, 1.51]
    R= np.linalg.matrix_rank(A)                 #求判断矩阵的秩
    V,D=np.linalg.eig(A)                     #求判断矩阵的特征值和特征向量，V特征值，D特征向量；
    list1 = list(V)
    B= np.max(list1)                            #最大特征值
    index = list1.index(B)
    C = D[:, index]                             #对应特征向量
    CI=(B-n)/(n-1)                             #计算一致性检验指标CI
    CR=CI/RI[n]
    if CR<0.10:
        print("CI=", CI.real)
        print("CR=", CR.real)
        print('对比矩阵A通过一致性检验，各向量权重向量Q为：')
        sum=np.sum(C)
        Q=C/sum                                #特征向量标准化
        print(Q.real)                                #    输出权重向量
        return Q.real
    else:
        print("对比矩阵A未通过一致性检验，需对对比矩阵A重新构造")
        return 0

 熵权分析法

 熵权分析法原理：

• “熵权”根据熵值大小，确定权重大小；用熵值和正向化消除量纲影响；熵权法是一个数据驱动的过程，必须有一定的数据量之后才能做正向化。
• 适用场景：具有主观判断的数据。

由于评价指标的好坏的规则多样化，没有统一化，有些指标越大越好，如成绩；有些越小越好，如房贷；有些在特定区间过高或过低都不佳，如血压；还有些存在最优值，偏差越大越差。若模型未经数据预处理直接计算，可能会出现问题。故，第一步是指标正向化。通过正向化，目标或结果的达成情况更加直观，提高指标的可解释性和可操作性。

• 对于极大型指标：指标越大越好，不需要正向化。只需要通过min-max规约或Z-score规约进行规约即可。

• 对于极小型指标：此类指标越小越好。它的正向化方式比较简单，可以取相反数；如果指标全部为正数，也可以取其倒数。

• 对于区间型指标：它的规约方法遵循下面的式子。

  {x\mathop{{}}\nolimits_{{new}}={ \left\{ {\begin{array}{*{20}{l}}{1-\frac{{a-x}}{{M}},x < a}\\{1,a \le x \le b}\\{1-\frac{{x-b}}{{M}},x > b}\end{array}}\right. }}

• 对于中值型指标：它的正向化操作为：

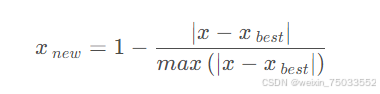
熵权法的计算步骤：

1. 构建m个事物n个评价指标的判断矩阵R（i=1，2，3,...n; j=1,2,...,m)。
2. 将判断矩阵归一化处理，得到新的归一化判断矩阵B。

   

3.  利用信息熵计算各指标的权重（为多指标评价提供依据），熵值e的计算如下：

   

4.  计算权重系数：

   

该式j代表属性j，第i类占样本比例；n代表属性j的取值数量。

•  熵权分析法的案例

在层次分析法案例的基础上采集了更多基站的数据，新的数据表格如下：

1.读取数据并对指标进行正向化：

1. pH值：这一列是区间型指标，可以将pH=7作为最优解，将这一列看作中间值型指标处理；与7偏差越大则得分越小。
2.  DO和鱼类密度都是极大型指标，剩下3个是极小型指标，所以用倒数的方法正向化。

以以上数据建立excel表：test；用代码正向化处理数据：

import pandas as pd

newdata=pd.read_excel("test.xlsx",sheet_name='Sheet1')

newdata['pH*']=1-abs(newdata['pH*']-7)

newdata['CODMn']=1/newdata['CODMn']

newdata['NH3-N']=1/newdata['NH3-N']

newdata['垃圾密度']=1/newdata['垃圾密度']

newdata=newdata.set_index('地点名称').dropna()

熵权法代码如下：

# Define entropyWeight function
def entropyWeight(data):
    data = np.array(data)
    # Normalize data
    P = data / data.sum(axis=0)
    # Calculate entropy
    E = np.nansum(-P * np.log(P) / np.log(len(data)), axis=0)
    # Calculate weight coefficients
    return (1 - E) / (1 - E).sum()

# Apply entropyWeight function to obtain weights
weights = entropyWeight(newdata)

print("Weights calculated using entropy method:")
print(weights)

调用函数后，我们可以得到权重分别为

（这个结果应该才是对的哈，笔者复现过了哟~） 

TOPSIS分析法

• 适用场景：有限多目标决策分析；
• TOPSIS分析法分为一般的和改进的； 
• 通过计算每个方案离理想解和负理想解的距离判断优劣，简化多个指标问题为距离问题。（理想解是最佳方案，各指标最优；负理想解是最差方案，各项指标最差。）

• TOPSIS分析法的基本思路：

1. 对原始决策方案进行归一化，找出最优方案和最劣方案
2. 对每一个决策计算其到最优方案和最劣方案的欧几里得距离
3. 计算相似度，方案与最优方案相似度越高则越优先。

对于距离，有多种方法可以计算它。例如：欧几里得距离、曼哈顿距离、余弦距离。

它们的计算方法如下：

• 欧几里得距离： $$ ${Euclidean \left( x,y \left) =\sqrt{{{\mathop{ \sum }\limits_{{i=1}}^{{n}}{ \left( x\mathop{{}}\nolimits_{{i}}-y\mathop{{}}\nolimits_{{i}} \left) \mathop{{}}\nolimits^{{2}}\right. \right. }}}}\right. \right. }$ $$
• 曼哈顿距离：

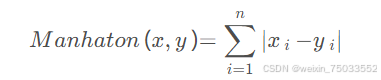
• 余弦距离：

  

  综上所述可得一般的TOPSIS分析法的基本流程如下：

1.对原始数据进行指标正向化和归一化，得到矩阵Z；

2.确定正理想解和负理想解：

3.计算各评价对象i（i=1，2，3...，402）到正理想解和负理想解的欧几里得距离Di：

4.计算各评价对象的相似度Wi：

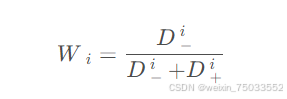
相似度值越大，离负理想解越远，越优先选择。

5.根据Wi大小排序得到结果。

改进的TPOSIS分析法：

考虑到不同指标在评价体系中的重要性存在差异，因此在计算距离时应该对各个指标赋予相应的权重。通常在解决TOPSIS问题时，我们会处理大量的数据，因此，权重可以通过数据驱动的熵权法来获得。

如果给每一个指标赋权重，权重向量记为w的话，距离公式应改为：

 TOPSIS分析法的案例

数据和熵权分析法案例的数据一样，实现TOPSIS代码如下：

#TOPSIS方法函数

def TOPSIS(A1,w):

    Z=np.array(A1)

    #计算正、负理想解

    Zmax=np.ones([1,A1.shape[1]],float)

    Zmin=np.ones([1,A1.shape[1]],float)

    for j in range(A1.shape[1]):

        if j==1:

          Zmax[0,j]=min(Z[:,j])

          Zmin[0,j]=max(Z[:,j])

        else:

          Zmax[0,j]=max(Z[:,j])

          Zmin[0,j]=min(Z[:,j])

  #计算各个方案的相对贴近度C

    C=[]

    for i in range(A1.shape[0]):

          Smax=np.sqrt(np.sum(w*np.square(Z[i,:]-Zmax[0,:])))

          Smin=np.sqrt(np.sum(w*np.square(Z[i,:]-Zmin[0,:])))

          C.append(Smin/(Smax+Smin))

    C=pd.DataFrame(C)

    return C

打印结果

# Apply TOPSIS function
topsis_results = TOPSIS(newdata, weights)

print("\nTOPSIS results:")
print(topsis_results)

代码结果：

 TOPSIS分析法的代码：熵权分析法代码+TOPSIS函数代码。

CRITIC方法

•  定性：基于数据波动性的客观赋权法，属于数据驱动的方法类型，需要数据量支持。
• 适用场景：数据稳定性可以作为一种信息并且分析的指标或因素之间有一定的关联关系的数据，即适用于具有明显客观标准的数据，但是如果数据中存在异常值或离群点，可能会对计算结果产生较大影响。
• 基思：波动性指标（对比强度）、冲突性指标（相关性）；波动性指标（对比强度）用标准差表示，数据标准差（波动）越大，权重越高；冲突性指标（相关性）用相关系数表示，指标之间的相关系数值越大（冲突性越小），那么其权重越低。权重计算时，对比强度同冲突性指标相乘，进行归一化处理后，得到最终的权重。

 CRITIC分析法的原理：

 统一指标好坏的标准，综合考虑对比强度和指标的变异程度，为每个指标赋予一个客观的权重。

CRITIC法的计算步骤：

假设有一个n个对象m项指标的数表

1.对指标进行无量纲化和正向化处理。用min-max规约进行无量纲化处理：如果这个指标是越大越好，那么规约方法形如：

如果指标是越小越好，那么规约方法形如：

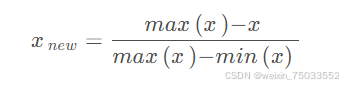
对于区间型和中值型指标，则可按照在TOPSIS分析法中讲到的指标正向化处理。

2.计算指标变异性（计算每一个指标在所有样本中的标准差Sj），标准差表示指标在样本中的差异波动情况，如果标准差越大，则它的区分度越明显，信号强度也越高，越应该给它分配更多权重。

3.计算指标冲突性，定义：

 其中rij​表示指标𝑖i和指标𝑗j之间的相关系数，严格意义上应该叫皮尔逊相关系数。其定义为:

 4.获取信息量（定义为指标变异性和冲突性的乘积）：

 5.归一化得到指标权重，再用权重乘以归一化的数据矩阵，得到每个对象的评分，并根据评分进行对象的评价、排序。归一化的过程形如：

CRITIC分析法的案例 

 还是用熵权分析法的数据，CRITIC分析法的代码：

def CRITIC(df):
  std_d=np.std(df,axis=1)
  mean_d=np.mean(df,axis=1)
  cor_d=np.corrcoef(df)
  # 也可以使用df.corr()
  w_j=(1-cor_d).sum(0) *std_d
  print(w_j)
  w=(mean_d/(1-mean_d)*w_j)/sum(mean_d/(1-mean_d)*w_j)
  print(w)

上述代码仅仅是采用CRITIC分析法计算出了权重，想要得到评分还要乘以归一化的数据矩阵。

模糊综合评价法 （教程少了重要公式，所以笔者这一块做不完整，虽然可以参考其他资料完善该模块，但是毕竟是数学导论的笔记，笔者认为应该还是以参考数学导论为主，所以这一模块不完整，请读者跳过此模块，待教程更新后，笔者也会把这一块补充完整，感谢读者的理解💖）

• 特点：结果清晰，系统性强。
• 适用场景：模糊，难以量化的问题，各种非确定性问题。

模糊综合分析法的原理：

• “模糊”概念：从属于该概念到不属于该概念之间无明显分界线，外延不清楚。举例：冷热，40度的水温可能女孩子洗澡觉得刚刚好，但是男生洗澡就会觉得有些烫。
• 模糊概念导致模糊现象，模糊数学就是用数学方法研究模糊现象。
• 模糊集：设U=u1，u2，...,um，U为刻画被评价对象的m种评价因素（评价指标）（由具体的指标体系所决定）。为了便于权重分配和评级，可以按评价因素的属性将评价因素分成若干类，把每一类都视为单一评价因素，称之为第一级评价因素。第一级评价因素可以设置下属的第二级评价因素，第二级评价因素又可以设置下属的第三级评价因素，依此类推，则U=U1∪U2∪…∪Us.(有限不交并)，其中𝑈𝑖=𝑢𝑖1,𝑢𝑖2,…，𝑢𝑖𝑚,𝑈𝑖∩𝑈𝑗=ΦUi=ui1,ui2,…，uim,Ui∩Uj=Φ,任意𝑖≠𝑗,𝑖,𝑗=1,2,…，𝑠i=j,i,j=1,2,…，s。我们称Ui是U的一个划分（部分），Ui称之为类（块）。设V=v1,v2，…,vn，是评价者对评价对象可能做出的各种总的评价结果组成的评价等级的集合；vj代表第j个评价结果，j=1，2，...,n。n为总的评价结果数，一般划分为3~5个等级。设A=（a1,a2,...,am)为权重（权数）分配模糊矢量，ai表示第i个因素的权重，要求0«ai,Σai=1。A反映了各因素的重要程度。
• 隶属度：一项指标对每个程度都分别进行评分（换句话说，这项指标被预判为某个程度的概率大小），是一个0到1之间的数。在实际中，，更多的是用德尔菲法也就是向多名相关领域专家发放问卷征求他们的意见以获得模糊评价，或是采取文献分析法从现有文献中找到模糊隶属度。但在短期内如果想要取得模糊隶属度，还可以根据具体的指标去推算，方法和TOPSIS中讲到的指标正向化一样。例如，我们如果获得了某种溶液的酸碱度PH值，它可能是越偏酸性越好，也可能是越偏碱性越好，也可能是在某个酸碱范围内最好。此时的隶属度计算也有不同的方式。
• 常见隶属度的计算模式：

  

• 模糊综合评价方法是借助模糊数学的隶属理论把定性评价转化为定量评价，即对受到多种因素制约的事物或对象做出一个总体的评价。
• 基思：用属于程度代替属于或不属于，刻画“中介状态”。1.确定被评价对象的因素（指标）集合评价（等级）集；2.确定各个因素的权重及它们的隶属度矢量，获得模糊评判矩阵；3.把模糊评判矩阵与因素的权矢量进行模糊运算并进行归一化，得到模糊综合评价结果。

秩和比分析（RSR)法 

• 适用场景：1.四格表资料的综合评价；2.n行m列资料的综合评价（一般都是这个场景）；3.计量资料和分类资料的综合评价。

• RSR法原理：

• 整次秩和比法：将n个评价对象的m个评价指标排列成n行m列的原始数据表。编出每个指标各评价对象的秩，效益型指标从小到大编秩（编秩即对数据排序，其顺序号作为秩），成本型指标从大到小编秩，同一指标数据相同者遍平均秩，得到秩矩阵，记为

  

•  非整次秩和比法：1.是一般秩和比法的扩展：在考虑部分模糊指标时，能正常对待可量化的指标，此外将线性模型改为指数、对数等其他情况后，也能做更多扩展。2.用类似于线性插值的方法对指标值进行编秩，以改进RSR法编秩的不足，所编秩次与原指标值之间存在定量的线性对应关系，克服了RSR法秩次化时易损失原指标值定量信息的缺点。
  对于正向指标：

  

  对于负向指标：

  

• 计算秩和比并排序：整次秩和比法中，只考虑元素的相对大小，不考虑具体值，计算秩和：

  

 

,wj​为第j个评价指标的权重，当指标权重相同时，wj=1/m，此时秩和可以表示为

如果只考虑排序问题，到这里的时候就可以知道结果了，以下步骤是为了能从正态分布角度对数据进行分层。 

• 确定RSR的分布：
• RSR的分布概念：指用概率单位Probit表达的值特定的累计频率。Probit模型是一种广义的线性模型，服从正态分布，其转换方法：

1. 编制RSR频数分布表，列出各组频数f，计算各组累计频数;
2. 确定各组RSR的秩次范围及平均秩次；
3. 计算累计频率 {{R} \overline /n \times 100\text{%}} ，最后一项记为1−1/(4*𝑛)​ 进行修正;
4. 将累计频率换算为概率单位Probit，Probit为累计频率对应的标准正态离差μ加3.

• 计算回归方程：以累积频率所对应的概率单位Probiti（i是下标）为自变量，以RSR值为因变量，计算直线回归方程，即：​ 

  

回归方程检验：对此回归方程，需要进行检验。回归方程的检验往往围绕以下几点展开：

• 残差独立性检验：Durbin-Watson 检验
• 方差齐性检验（异方差性）：Breusch-Pagan 检验和 White 检验
• 回归系数𝑏b的有效性检验： 𝑡t检验法和置信区间检验法
• 拟合优度检验：(自由度校正)决定系数、Pearson相关系数、Spearman秩相关系数、交叉验证法等
  此外建议进行回归系数b的t检验及拟合优度的Pearson相关系数检验即可
• 计算校正RSR值，并进行分档排序：按照回归方程推算所对应的RSR估计值对评价对象进行分档排序，分档数由研究者根据实际情况决定；目的：将数据按照秩的各种情况，映射到正态分布曲线上，结合正态分布的相关划分方法进行分档。

  

• RSR法的步骤：

1. 判断指标类型，进行排序（对效益型指标进行从小到大的排序；对成本型指标进行从大到小的排序），并计算每个指标的秩次；
2. 计算每个指标的秩和比（RSR)，作为无量纲的统计量；
3. 基于秩和比进行统计分析，研究其分布情况；
4. 根据RSR值对评价对象进行直接排序或分档排序，以评估其综合表现。

• RSR法的优缺点：
• 优点：是非参数统计分析，对指标的选择无特殊要求，适用于各种评价对象；可以消除异常值的干扰（因为计算用的数值是秩次），融合了参数分析的方法，结果比单纯采用非参数法更为精确，既可以直接排序又可以分档排序，使用范围广泛。
• 缺点：会失去一些原始数据的信息（因为排序的主要依据是利用原始数据的秩次，最终算得的RSR反映的是综合秩次的差距，而与原始数据顺位间的差距程度大小无关）；当RSR值不满足正态分布时，分档归类的结果与实际情况有偏差，且分档归类的结果只能回答分级程度是否有差别。

秩和比分析法案例

数据如下：

秩和比分析法案例的代码如下：

import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy.stats import norm


def rsr(data, weight=None, threshold=None, full_rank=True):
  Result = pd.DataFrame()
  n, m = data.shape

  # 对原始数据编秩
  if full_rank:
    for i, X in enumerate(data.columns):
      Result[f'X{str(i + 1)}：{X}'] = data.iloc[:, i]
      Result[f'R{str(i + 1)}：{X}'] = data.iloc[:, i].rank(method="dense")
  else:
    for i, X in enumerate(data.columns):
      Result[f'X{str(i + 1)}：{X}'] = data.iloc[:, i]
      Result[f'R{str(i + 1)}：{X}'] = 1 + (n - 1) * (data.iloc[:, i].max() - data.iloc[:, i]) / (data.iloc[:, i].max() - data.iloc[:, i].min())

  # 计算秩和比
  weight = 1 / m if weight is None else np.array(weight) / sum(weight)
  Result['RSR'] = (Result.iloc[:, 1::2] * weight).sum(axis=1) / n
  Result['RSR_Rank'] = Result['RSR'].rank(ascending=False)

  # 绘制 RSR 分布表
  RSR = Result['RSR']
  RSR_RANK_DICT = dict(zip(RSR.values, RSR.rank().values))
  Distribution = pd.DataFrame(index=sorted(RSR.unique()))
  Distribution['f'] = RSR.value_counts().sort_index()
  Distribution['Σ f'] = Distribution['f'].cumsum()
  Distribution[r'\bar{R} f'] = [RSR_RANK_DICT[i] for i in Distribution.index]
  Distribution[r'\bar{R}/n*100%'] = Distribution[r'\bar{R} f'] / n
  Distribution.iat[-1, -1] = 1 - 1 / (4 * n)
  Distribution['Probit'] = 5 - norm.isf(Distribution.iloc[:, -1])

  # 计算回归方差并进行回归分析
  r0 = np.polyfit(Distribution['Probit'], Distribution.index, deg=1)
  print(sm.OLS(Distribution.index, sm.add_constant(Distribution['Probit'])).fit().summary())
  if r0[1] > 0:
    print(f"\n回归直线方程为：y = {r0[0]} Probit + {r0[1]}")
  else:
    print(f"\n回归直线方程为：y = {r0[0]} Probit - {abs(r0[1])}")

  # 代入回归方程并分档排序
  Result['Probit'] = Result['RSR'].apply(lambda item: Distribution.at[item, 'Probit'])
  Result['RSR Regression'] = np.polyval(r0, Result['Probit'])
  threshold = np.polyval(r0, [2, 4, 6, 8]) if threshold is None else np.polyval(r0, threshold)
  Result['Level'] = pd.cut(Result['RSR Regression'], threshold, labels=range(len(threshold) - 1, 0, -1))

  return Result, Distribution


def rsrAnalysis(data, file_name=None, **kwargs):
  Result, Distribution = rsr(data, **kwargs)
  file_name = 'RSR 分析结果报告.xlsx' if file_name is None else file_name + '.xlsx'
  Excel_Writer = pd.ExcelWriter(file_name)
  Result.to_excel(Excel_Writer, '综合评价结果')
  Result.sort_values(by='Level', ascending=False).to_excel(Excel_Writer, '分档排序结果')
  Distribution.to_excel(Excel_Writer, 'RSR分布表')
  Excel_Writer.save()

  return Result, Distribution

data = pd.DataFrame({'产前检查率': [99.54, 96.52, 99.36, 92.83, 91.71, 95.35, 96.09, 99.27, 94.76, 84.80],
                     '孕妇死亡率': [60.27, 59.67, 43.91, 58.99, 35.40, 44.71, 49.81, 31.69, 22.91, 81.49],
                     '围产儿死亡率': [16.15, 20.10, 15.60, 17.04, 15.01, 13.93, 17.43, 13.89, 19.87, 23.63]},
                    index=list('ABCDEFGHIJ'), columns=['产前检查率', '孕妇死亡率', '围产儿死亡率'])
data["孕妇死亡率"] = 1 / data["孕妇死亡率"]
data["围产儿死亡率"] = 1 / data["围产儿死亡率"]
rsr(data)

代码结果如下：

主成分分析法 

• 适用场景：想将问题中过于过于精细化的变量抽象出更高一级的变量去描述数据（以线性加权的方式去抽象出新变量，难以对变量背后的东西进行解释），同时还能保持数据信息尽可能少地丢失。
• 在数据处理和评价中有很大的应用。

主成分分析法原理：

在PRITIC方法一节中我们看到了一个事实：数据列之间是存在关联的。例如，在分析数据时，有一列数据是用kg表示的重量，一列数据是用g表示的重量，两列数据的信息是一样的，所以完全可以去掉其中一列。这是个极限情况，但是事实上数据中确实可能存在相关性很高的几列，原本10列的数据集，实际上用3列就有可能表示了。如果能够通过删减或变换的方式减少列数，那么处理的难度可就大大减小了。这种操作被称为降维。另外，即使不去减少列表，削弱相关性也是很重要的操作。（也是降维的一种操作）

• 主成分分析法主要目的：

1. 数据的降维：用较少的变量去解释原来资料中的大部分变异，将原始数据中许多相关性较高的变量转化成彼此相互独立或不相关的变量；
2. 主成分的解释：选出比原始变量个数少，能解释大部分资料中变异的几个新变量（也就是主成分）。

•  主成分分析法的步骤：

1. 数据的去中心化：对数据表X中每个属性减去这一列的均值。（目的：消除数据平均水平对它的影响）

   

2. 求协方差矩阵：

   

3.  对协方差矩阵进行特征值分解：

   

4. 特征值排序：挑选更大的k个特征值，将特征向量组成矩阵P。
5. 进行线性变换F=PX，从而得到主成分分析后矩阵。矩阵中的每一列称作一个主成分，选择的特征值经过归一化就变成了权重。 

 注意：实际过程中PCA（主成分分析）的底层做矩阵分解时使用奇异值分解（SVD）更多一些，这里用特征值分解更加容易理解。

主成分分析法的案例

首先，我们通过鸢尾花数据集的例子来看到它是如何减少数据列数的。鸢尾花数据集是一个在机器学习和统计学领域广泛使用的经典数据集。它包含了150个样本，每个样本有4个特征：萼片长度、萼片宽度、花瓣长度和花瓣宽度，这四个特征都是以厘米为单位。这些特征用于描述鸢尾花的外观。数据集中的样本分为三类，每类50个样本，分别代表山鸢尾、变色鸢尾和维吉尼亚鸢尾三种不同的鸢尾属植物。这个数据集在第9章会被再一次搬上舞台，这里主要是测试主成分分析法。

• 通过sklearn.datasets的接口导入数据，可以发现其中有四列自变量，再使用sklearn.decomposition提供的PCA函数进行主成分分析即可。代码形如：

import matplotlib.pyplot as plt
import sklearn.decomposition as dp
from sklearn.datasets import load_iris
x,y=load_iris(return_X_y=True) #加载数据，x表示数据集中的属性数据，y表示数据标签
pca=dp.PCA(n_components=0.99) #加载pca算法，设置降维后主成分数目为2
reduced_x=pca.fit_transform(x,y) #对原始数据进行降维，保存在reduced_x中
red_x,red_y=[],[]
blue_x,blue_y=[],[]
green_x,green_y=[],[]
for i in range(len(reduced_x)): #按鸢尾花的类别将降维后的数据点保存在不同的表表中
    if y[i]==0:
           red_x.append(reduced_x[i][0])
       	red_y.append(reduced_x[i][1])
      elif y[i]==1:
           blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])
  else:
       green_x.append(reduced_x[i][0])
       green_y.append(reduced_x[i][1])
plt.scatter(red_x,red_y,c='r',marker='x')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()

 这里参数中PCA的参数设置有两种方法：如果n_components为整数，说明希望取到几个主成分；如果为小数，则说明希望保留多少的信息量，也就是取前几个特征值它们的和能够超过参数给定的阈值。

代码结果如下：

• 主成分分析法如何应用于评价呢？其实非常简单，将所有的主成分乘上对应的权重就可以得到最终的评分了，也就是：

  

  我们回到TOPSIS分析法的案例数据，如果想使用主成分分析法对数据进行综合评价，可以怎么做呢？首先，在经过数据的正向化和归一化以后，可以手动实现PCA如下：

def pca(X,n_components):
  X=np.array(X)
  X=X-np.mean(X)
  n=len(X)
  A=np.dot(X.T,X)/(n-1)
  V,D=np.linalg.eig(A)
  idx = (-V).argsort(axis=None)[:n_components]
  P=D[idx]
  F=np.dot(X,P.T)
  return V[idx]/sum(V),F

还要在加上这段代码，才能搞出评分：

 

# Convert relevant columns to numeric (if needed)
columns_to_process = ['pH*', 'CODMn', 'NH3-N', '垃圾密度']
newdata[columns_to_process] = newdata[columns_to_process].apply(pd.to_numeric)

# Perform PCA on selected columns
n_components = 2  # Number of principal components to retain
_, newdata_pca = pca(newdata[columns_to_process], n_components)

# Add PCA results back to the DataFrame
for i in range(n_components):
    newdata[f'PCA_{i+1}'] = newdata_pca[:, i]

# Print or return the modified DataFrame
print(newdata)

代码结果如下：

 在使用同样的正向化和归一化手段以后，可以给出对应的主成分评分。值得注意的是，主成分评分可能会出现负数，但并不影响。得分越高则说明评价结果越好，越低甚至为负数则评价结果越差。

因子分析法

因子分析法的原理：

• 巴雷特特球形检验（Barlett's Test）：

1. 适用场景：检验多个变量之间是否存在相关性，从而决定是否适合进行因子分析，如果得到到统计概率<0.05，则适合做因子分析；
2. 基本思想：如果多个变量之间彼此独立，那么它们的方差应该与它们的相关系数矩阵的行列式值成正比。如果实际观察到的行列式值与预期的行列式值相差很大，那么可以认为这些变量之间存在相关性。通过比较实际观察到的行列式值与预期的行列式值，我们可以决定是否拒绝零假设，即这些变量是独立的。

• KMO检验：

1. 适用场景：检测数据是否符合因子分析的基本假设，即变量之间应该呈现出一定程度的相关性。
2. 基本思想：通过比较变量之间的简单相关系数和偏相关系数来进行评估。通过计算这些相关系数的平方和来比较这两种关系，以确定数据是否适合进行因子分析。KMO统计量的取值范围在0-1之间。当KMO值越接近1时，表示变量间的相关性越强，原有变量越适合作因子分析；当KMO值越接近0时，表示变量间的相关性越弱，原有变量越不适合作因子分析。在实际分析中，KMO统计量在0.7以上时效果比较好；当KMO统计量在0.5以下时，则不适合应用因子分析法，可能需要重新设计变量结构或者采用其他统计分析方法。

 如果能够通过这两个检验中的一个，就可以开始做因子分析了。

因子分析步骤：

1. 选出一组变量来进行因子分析。选择的方法有两种：定性和定量。如果原始变量之间的相关性不好，那它们就很难被分解成几个公共因子。所以，原始变量之间应该有较强的相关性。

2. 计算这些选定的原始变量的相关系数矩阵。这个矩阵能告诉我们各个变量之间的关系是什么样的。这一步特别重要，因为如果变量之间没什么关系，那把它们分解成几个因子就没什么意义了。这个相关系数矩阵也是我们进行因子分析的基础。

3. 从这些原始变量中提取出公共因子。具体要提取几个，需要我们来做决定。这个决定可以基于我们的先验知识或者实验假设。不过，通常我们会看提取的因子的累计方差贡献率是多少。一般来说，累计的方差贡献率达到70%或以上，就算是满足了要求。

4. 对提取出来的公共因子进行旋转。这样做的目的是为了让因子的意义更明确，更容易理解。

5. 计算出因子的得分。这些得分可以在后续的研究中使用，比如在因子回归模型中。这样，我们就能更好地理解这些变量的关系，并找出影响结果的关键因素。

• 因子载荷矩阵是因子分析中的核心概念之一，它描述了变量与因子之间的关系。因子载荷矩阵中各列元素的平方和成为对所有的变量的方差贡献和，衡量了各个公共因子的相对重要性。因子载荷矩阵是可逆的，因此可以用于将原始变量表示为公共因子和特殊因子的线性组合。这使得我们可以利用公共因子解释原始数据的结构和模式，并对其进行解释和分析。因子载荷矩阵在因子分析中具有重要的作用，它不仅用于确定公共因子和特殊因子的数量，还可以用于估计公共因子和特殊因子的系数。在实际中，可以使用主成分分析法等方法估计因子载荷矩阵。

• 因子载荷是第i个变量与第j个公共因子的相关系数，反映了第i个变量和第j个公共因子之间的重要性，绝对值越大，表示相关性的密切程度越高。

• 为什么需要进行因子旋转？假设我们有一个市场调研数据集，其中包括了多个产品特性和消费者对产品的评价。通过因子分析，我们希望找出影响消费者评价的公共因子。初始的因子载荷矩阵可能显示出一些不太直观的结果，例如某些产品特性与公共因子之间的关系不太明显。这时，通过因子旋转，我们可以对原始因子进行转换，使得因子载荷矩阵中的因子载荷的绝对值更加接近于1或0。这样，我们可以更清楚地看出哪些产品特性与公共因子有强烈的关联，哪些特性的影响较小。

• 因子旋转的本质就是做一个正交变换，让因子载荷阵的结构得到简化。常见的因子旋转方法包括方差最大法等。

• 最终得到的因子得分往往比主成分分析更加具有可解释性。它在人文社会科学的问题中有着非常重要的应用。前面学习的一系列方法例如层次分析法、熵权法等把评价的重点放在了指标权重上，TOPSIS分析法等把重点放在了得分折算上。但因子分析走出了第三条路径：通过构造因子，将多个变量进行抽象构造出指标体系（可以理解为，数据中给出的的二级指标，而通过因子分析可以给出一级指标以及指标对应关系）。良好的可解释性就意味着它可以深度地和一些人文社会科学理论融合起来，并具有广阔的后续应用空间。在第9章中我们会再一次提到因子分析的扩展方法：结构方程。

• 因子分析法的案例

因子分析分为探索型因子分析和验证型因子分析。探索性因子分析是从数据出发，寻找能获得最大解释性的因子数量；而验证型因子分析则是研究之前已经提出了理论假设，现在需要用实验数据佐证。Python可以使用factor_analyzer实现：

我们从国家统计局获取了自2005—2012年间各类学校的生师比（学生数量与教师数量的比值），数据如表5.9所示，试对数据进行因子分析并进行一定解释。

 这是一个非常典型的社会科学问题。我们这里提出了假说：问题可以被分解为三个因子。但首先，我们需要对数据进行预处理：

import pandas as pd

import numpy as np

data=pd.read_csv("查询数据.csv",encoding='utf-8')

data=data.interpolate('linear')

data=data.fillna(method='bfill')

newdata=data[['小学生师比', '初中生师比',
'普通高中生师比', '职业高中生师比',
'本科院校生师比', '专科院校生师比',
]]

通过插值与填充，我们对数据中的空缺进行了处理。下面对数据进行巴雷特球形检验和KMO检验：

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
import math
from sklearn.decomposition import FactorAnalysis
from scipy.stats import bartlett

plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
plt.style.use("ggplot")

n_factors = 3  # 因子数量

cols = ['小学生师比', '初中生师比',
'普通高中生师比', '职业高中生师比',
'本科院校生师比', '专科院校生师比',]

# 准备数据
df = newdata[cols]

# 巴雷特方法
corr = list(df.corr().to_numpy())
print(bartlett(*corr))

# KMO方法
def kmo(dataset_corr):
    corr_inv = np.linalg.inv(dataset_corr)
    nrow_inv_corr, ncol_inv_corr = dataset_corr.shape
    A = np.ones((nrow_inv_corr, ncol_inv_corr))
    for i in range(nrow_inv_corr):
        for j in range(i, ncol_inv_corr, 1):
            A[i, j] = -(corr_inv[i, j]) / (math.sqrt(corr_inv[i, i] * corr_inv[j, j]))
            A[j, i] = A[i, j]
    dataset_corr = np.asarray(dataset_corr)
    kmo_num = np.sum(np.square(dataset_corr)) - np.sum(np.square(np.diagonal(A)))
    kmo_denom = kmo_num + np.sum(np.square(A)) - np.sum(np.square(np.diagonal(A)))
    kmo_value = kmo_num / kmo_denom
    return kmo_value

print(kmo(newdata[cols].corr().to_numpy()))

 结果如下：

随后调用分析器并给出载荷矩阵：

# 因子分析
fa = FactorAnalysis(n_components=n_factors, rotation='varimax')
fa.fit(newdata[cols])

loadings = fa.components_.T
communalities = np.sum(np.square(loadings), axis=1)

# 绘制热力图
plt.figure(figsize=(9, 6))
ax = sns.heatmap(loadings, annot=True, cmap="BuPu")
ax.set_xticklabels(['基础教育', '职业教育', '高等教育'], rotation=0)
ax.set_yticklabels(cols, rotation=0)
plt.title('因子分析')
plt.show()

# 因子贡献率
total_variance = np.var(newdata[cols], axis=0).sum()
explained_variance = np.var(np.dot(fa.transform(newdata[cols]), fa.components_), axis=0).sum()
factor_variance = explained_variance / total_variance
print("因子贡献率:", factor_variance)

# 计算因子得分
fa_score = fa.transform(newdata[cols])
complex_score = np.dot(fa_score, fa.components_)

 给出的载荷矩阵如下：

 我们可以看到，三列因子的累计解释率能到0.9以上，说明非常好。而这三列根据颜色的对应关系，可以看到第一列对应了小学、初中、高中，我们可以命名为基础教育；第二列对应职高、中专、大专，可以命名为职业教育；第三列对应普通高校和本科，可以命名为高等教育。可解释性确实是非常强，并且这样我们就构成了一个指标体系的对应关系。

因子分析和主成分分析虽然都是用于评价模型的方法，但二者有很大的不同：

• 原理不同：主成分分析是利用降维(线性变换)的思想，每个主成分都是原始变量的线性组合，使得主成分比原始变量具有某些更优越的性能，从而达到简化系统结构，抓住问题实质的目的。而因子分析更倾向于从数据出发，描述原始变量的相关关系，将原始变量进行分解。

• 线性表示方向不同：主成分分析中是把主成分表示成各变量的线性组合，而因子分析是把变量表示成各公因子的线性组合。说白了，一个是组合，一个是分解。

• 假设条件不同：因子分析需要一些假设。因子分析的假设包括：各个共同因子之间不相关，特殊因子之间也不相关，共同因子和特殊因子之间也不相关。

• 分析的主要数据量不同：主成分分析的主成分的数量是一定的，一般有几个变量就有几个主成分(只是主成分所解释的信息量不等)，实际应用时会根据帕累托图提取前几个主要的主成分。而因子分析的因子个数需要分析者指定，指定的因子数量不同而结果也不同。

• 应用范围不同：在实际的应用过程中，主成分分析常被用作达到目的的中间手段，而非完全的一种分析方法，提取出来的主成分无法清晰的解释其代表的含义。而因子分析就是一种完全的分析方法，可确切的得出公共因子。

数据包络分析法

•  数据包络分析是 A.Charnes, W.W.Copper 和 E.Rhodes 在 1978 年提出的评价多指标输入输出，衡量系统有效性的方法。将属性划分为投入项、产出项（成本型、效益型指标），不预先设定权重，只关心总产出与总投入，以其比率作为相对效率。
• CCR数据包络模型：

  数据包络分析其实是一系列方法的总称，它指的就是通过分析成本指标和收益指标给出效率评价的一系列方法。数据包络分析包括CCR, BBC等多种方法。首先我们介绍CCR方法。假设现在有m个投入型指标X，s个产出型指标Y，n个比较对象，数据包络的目的就是评价这些对象的“性价比”，也就是投入少一些、产出多一些。

  与先前的一些评价类模型一样，数据包络中的CCR模型其目的也是获得权重。只不过，分别对产出型指标和投入型指标构造权重向量𝑢u和𝑣v，而定义投入产出比，问题的本质是解一个规划模型。对于每一个样本而言，有：

  

• {s.t.{ \left\{ {\begin{array}{*{20}{l}}{\frac{{u\mathop{{}}\nolimits^{{T}}y\mathop{{}}\nolimits_{{i}}}}{{v\mathop{{}}\nolimits^{{T}}x\mathop{{}}\nolimits_{{i}}}} \le 1}\\{u,v\text{ } \ge 0}\end{array}}\right. }}

  这一规划的目的是让投入产出比尽可能大，因为分母表示投入，分子表示产出，这个值越大，表示这一项的“性价比”越高。但投入产出比根据常理判断，不可能超过100%，所以加上了不能超过100%的约束。

  这显然是一个非线性规划模型，但可以转化为一个线性规划问题求解。事实上，希望一个分式越大，只需分子越大的同时分母越小即可。如果不能同时做到这两点，也可以通过限制的方法让分母为一个定值。因此，对于样本k，可以有这样一个形式来改写： {s.t.{ \left\{ {\begin{array}{*{20}{l}}{{\mathop{ \sum }\limits_{{i=1}}^{{n}}{ \lambda \mathop{{}}\nolimits_{{i}}x\mathop{{}}\nolimits_{{ij}} \le OE\mathop{{}}\nolimits_{{k}}∙x\mathop{{}}\nolimits_{{kj}}\text{ }\text{ }\text{ } \forall j=1,2, \cdots ,m\mathop{{}}\nolimits_{{1}}}}}\\{{\mathop{ \sum }\limits_{{i=1}}^{{n}}{ \lambda \mathop{{}}\nolimits_{{i}}}}y\mathop{{}}\nolimits_{{ij}} \ge y\mathop{{}}\nolimits_{{kj}}\text{ } \forall j=1,2, \cdots ,m\mathop{{}}\nolimits_{{2}}\text{ }\text{ }\text{ }\text{ }}\\{ \lambda \mathop{{}}\nolimits_{{i}} \ge 0,\text{ }i=1,2,{ \cdots ,}n}\end{array}}\right. }} 在不同的生产规模下，规模报酬将会随之改变。生产规模小时，投入产出比会随着规模增加而迅速提升，称为规模报酬递增；当生产达到高峰期时，产出与规模成正比而达到最适生产规模，称为规模报酬固定；当生产规模过于庞大时，产出减缓，则称为规模报酬递减，也就是投入增加时，产出增加的比例会少于投入增加的比例。分析递增与递减是通过lambda的和发现的，当lambda的和为1的时候规模报酬固定；大于1则递增，小于1则递减。

• BBC数据包络模型：

  BBC模式是对CCR的改进。BCC模型是从产出的角度探讨效率，即在相同的投入水准下，比较产出资源的达成情况，这种模式称为“投入导向模式”。所得到的是“技术效益”，DEA=1称为“技术有效”。实质上，就是投入可持续增加，研究投入和产出的变化关系。

  BCC模型的基本形式如下 {s.t.{ \left\{ {\begin{array}{*{20}{l}}{{\mathop{ \sum }\limits_{{j=1}}^{{n}}{ \lambda \mathop{{}}\nolimits_{{j}}y\mathop{{}}\nolimits_{{ij}}}} \le \theta \mathop{{}}\nolimits_{{i}}x\mathop{{}}\nolimits_{{i}}}\\{{\mathop{ \sum }\limits_{{j=1}}^{{n}}{ \lambda \mathop{{}}\nolimits_{{i}}}}y\mathop{{}}\nolimits_{{ij}} \ge \theta \mathop{{}}\nolimits_{{i}}y\mathop{{}}\nolimits_{{i}}\text{ }\text{ }\text{ }\text{ }}\\{{\mathop{ \sum }\limits_{{j=1}}^{{n}}{ \lambda \mathop{{}}\nolimits_{{j}}}}=1}\end{array}}\right. }} 这个问题的本质也是在求解一个规划问题，主要的目的是求解λ和***θ***。但BCC模型应用相对较少，能够掌握CCR模型的解决方法即可。

 数据包络模型的实现：

这里我们实现数据包络模型中的CCR方法，并以面向对象的方法进行封装：

import numpy as np

from scipy.optimize import fmin_slsqp

 

class DEA(object):

  def __init__(self, inputs, outputs):

    # supplied data

    self.inputs = inputs

    self.outputs = outputs

    # parameters

    self.n = inputs.shape[0]

    self.m = inputs.shape[1]

    self.r = outputs.shape[1]

    # iterators

    self.unit_ = range(self.n)

    self.input_ = range(self.m)

    self.output_ = range(self.r)

    # result arrays

    self.output_w = np.zeros((self.r, 1), dtype=np.float)  # output weights

    self.input_w = np.zeros((self.m, 1), dtype=np.float)  # input weights

    self.lambdas = np.zeros((self.n, 1), dtype=np.float)  # unit efficiencies

    self.efficiency = np.zeros_like(self.lambdas)  # thetas

  def __efficiency(self, unit):

    # compute efficiency

    denominator = np.dot(self.inputs, self.input_w)

    numerator = np.dot(self.outputs, self.output_w)

    return (numerator/denominator)[unit]

  def __target(self, x, unit):

    in_w, out_w, lambdas = x[:self.m], x[self.m:(self.m+self.r)], x[(self.m+self.r):]  # unroll the weights

    denominator = np.dot(self.inputs[unit], in_w)

    numerator = np.dot(self.outputs[unit], out_w)

    return numerator/denominator

  def __constraints(self, x, unit):

    in_w, out_w, lambdas = x[:self.m], x[self.m:(self.m+self.r)], x[(self.m+self.r):]  # unroll the weights

    constr = []  # init the constraint array

    # for each input, lambdas with inputs

    for input in self.input_:

      t = self.__target(x, unit)

      lhs = np.dot(self.inputs[:, input], lambdas)

      cons = t*self.inputs[unit, input] - lhs

      constr.append(cons)

    # for each output, lambdas with outputs

   for output in self.output_:

      lhs = np.dot(self.outputs[:, output], lambdas)

      cons = lhs - self.outputs[unit, output]

      constr.append(cons)

    # for each unit

    for u in self.unit_:

      constr.append(lambdas[u])

    return np.array(constr)

  def __optimize(self):

    d0 = self.m + self.r + self.n

    # iterate over units

    for unit in self.unit_:

      # weights

      x0 = np.random.rand(d0) - 0.5
      x0 = fmin_slsqp(self.__target, x0, f_ieqcons=self.__constraints, args=(unit,),disp=False)

      # unroll weights

      self.input_w, self.output_w, self.lambdas = x0[:self.m], x0[self.m:(self.m+self.r)], x0[(self.m+self.r):]

      self.efficiency[unit] = self.__efficiency(unit)

  def fit(self):

    self.__optimize()  # optimize

    return self.efficiency

在这里我们给出一系列测试用例，若第1到4列为投入指标，第5到11列为产出指标，测试每个对象的投入产出效率如下：

# 定义输入和输出数据  

data = np.array([[39414, 2823, 34877, 44562, 2036, 603, 322, 934936, 929914, 1492, 29811],  

       [54934, 1911, 52242, 35262, 3862, 908, 396, 1075563, 1030664, 1780, 29811],  

      [96442, 2743, 88737, 303221, 4307, 1596, 694, 1104835, 1010146, 1936, 32678],  

       [107079, 3036, 98513, 478883, 3956, 2530, 1089, 909220, 862077, 2160, 36063],  

      [124359, 3326, 116897, 378318, 4102, 2669, 1179, 1117851, 1123109, 2349, 38951],  

       [140167, 3900, 130355, 261203, 4180, 3538, 1991, 1116429, 1100510, 2446, 40324],  

       [161523, 3989, 153722, 444755, 4309, 3727, 1593, 878466, 880226, 2637, 43211],  

       [177681, 4669, 167161, 422267, 4630, 6629, 1867, 1048053, 1003952, 2904, 47116],  

       [124969, 4416, 111415, 286399, 3829, 5665, 2591, 1142395, 1112661, 3092, 49406]])

X=data[:,0:4]

y=data[:,5:11]

dea = DEA(X,y)

rs = dea.fit()

print(rs)

 从结果上来看，这些样本中有多个样本的投入产出比能达到1，说明它们的效率是比较高的。而对于没有达到1的样本，则需要进一步分析它们的规模报酬是哪一种类型。

评价模型总结

• 指标体系的构建：综合评价是针对研究的对象,建立一个进行测评的指标体系,利用一定的方法或模型,对搜集的资料进行分析,对被评价的事物作出定量化的总体判断。
• 从前面这些评价类模型的性质来看，评价类模型的核心就是三个：指标体系，权重计算，评分规则。一个好的指标体系是计算权重和评分的基础。如果没有一个好的指标体系，我们就无法对问题做出客观全面准确的评价，也无法使用前面讲述的评价类模型。

• 构建好的指标体系需要遵循以下几个步骤：

• 明确目标与目的：首先需要明确指标体系的目标和目的，以确保所选择的指标与所需评估的目标紧密相关。这涉及到确定要评估哪些方面的表现、期望达到的水平以及衡量这些评分的标准。

• 收集数据和信息：为了准确地度量和评估，需要收集相关数据和信息。这些数据可以来自问题本身，也可以查找文献。在数据收集过程中，需要注意数据的可靠性和完整性，以确保指标的可信度和有效性。

• 选择合适的指标：选择合适的关键指标对于构建有效的指标体系至关重要。指标应该具有可操作性、关联性和可靠性。可操作性是指指标应该易于测量和计算；关联性是指指标之间应该有密切的相关性或因果关系；可靠性是指指标应该是稳定和可重复的。

• 建立权重和优先级：为了更好地反映实际情况，需要为每个指标分配一定的权重和优先级。权重可以根据不同因素的重要性而定，比如财务指标可能比非财务指标更重要。而优先级的设定则需要根据组织的战略目标和重点关注领域来确定。

• 反馈和沟通：评价模型只是第一步，更重要的是要将结果进行阐述与分析，把它好理论结合起来。同时，在实际应用中不断优化指标体系，使其更加贴近实际需求。

• 两大核心：权重生成与得分评价：

• 权重和评分是评价类模型计算中最重要的两个部分。前面的一些方法已经给大家展示了权重的计算方法例如基于熵值、相关系数与方差、成对比较矩阵等，也有计算方法例如加权求和、计算距离、模糊隶属度等。

  针对具体问题选择合适的评价类模型，需要考虑以下几个因素：

• 问题类型和数据类型：不同的评价类模型适用于不同的问题类型和数据类型。例如，层次分析法适用于定性与定量相结合的问题，模糊综合评价法适用于模糊性较强的问题，主成分分析法和因子分析法适用于高维度的数据降维问题。因此，需要根据问题的性质和数据类型选择合适的评价类模型。

• 数据量和分析需求：不同评价类模型对数据量和数据分析需求也不同。例如，熵权法需要大量的数据才能准确地计算出各个指标的权重，而因子分析法则需要较少的样本量来分析数据。因此，需要根据具体的数据量和数据分析需求选择合适的评价类模型。

• 算法复杂度和可操作性：不同的评价类模型算法复杂度不同，所需的计算资源和操作难度也不同。例如，主成分分析法需要较为复杂的数学推导和计算，而熵权法则相对简单易懂。因此，需要根据具体的应用场景和计算资源选择合适的评价类模型。

• 指标数量和权重分配：在选择评价类模型时，需要考虑指标数量和权重分配的问题。如果指标数量较多或者权重分配比较复杂，需要选择能够处理这些问题的评价类模型。例如，熵权法则可以通过熵值来判断各个指标的离散程度，从而确定各个指标的权重。

• 主观与客观因素：不同的评价类模型在处理主观与客观因素时有所不同。例如，层次分析法和模糊综合评价法可以较好地处理主观因素，而熵权法和CRITIC法则更加注重客观因素的考虑。因此，在选择评价类模型时，需要根据具体的问题和实际情况选择能够处理主观与客观因素的评价类模型。