上面几节讲了监督学习和非监督学习的一些算法(目前还不完整,会慢慢补充哒)
如果文章内容有错误,欢迎小伙伴在评论区指出!
前言:
损失函数在机器学习中非常重要,直接关乎模型的好坏(so?学好它)。
其实第二节讲了这个最小二乘法,他的思想是使用残差和作为他的损失函数,来度量这个模型好不好,往哪个方向更新。通过最小化这个损失值,我们可以驱使模型不断学习和改进,直至达到满意的预测精度。
概念:
损失函数是一个量化模型预测错误的数学工具。
拓展:
我们常常在机器学习中听到成本函数。那两个有什么关系呢?
损失函数用于训练单个样本,也被成为误差训练。
成本函数用于训练整个数据集的平均损失。而我们的优化策略就是想让成本函数最小。
1、基于距离度量的损失函数
1.1 欧氏距离损失(Euclidean Distance Loss)
概念:
衡量模型输出值与真实值之间的欧式距离。
就是我们平时说的“距离”。
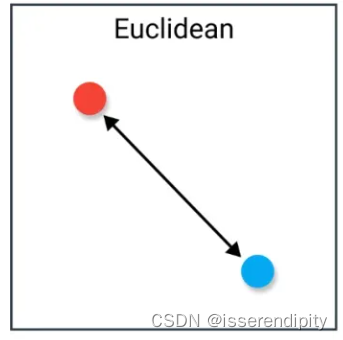
这个很简单,就不多说啦,一看就明白啦。
用法:
适用于低维数据,最常用的距离方法之一。
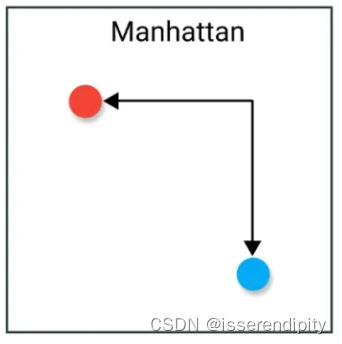
1.2 曼哈顿距离损失(Manhattan Distance Loss)
概念:
衡量模型输出值与真实值之间的曼哈顿距离,也称为 范式距离。
通常称为出租车距离或城市街区距离( Taxicab distance or City Block distance)
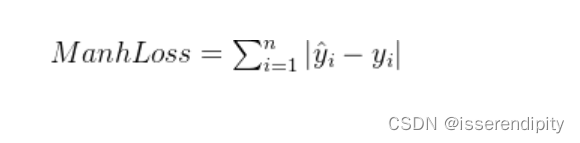
只能直角移动,不能在对角线上移动。
用法:
适用于高维数据但是不直观!
Lasso算法就用了这个L1范式(这里有讲lasso算法)
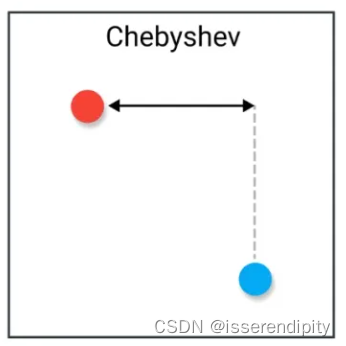
1.3 切比雪夫距离损失(Chebyshev Distance Loss)
概念:
衡量模型输出值与真实值之间的切比雪夫距离,即两个向量各维度差的最大值。
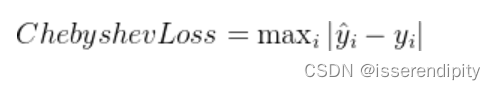
距离计算就是像这样的。
用法:
这个比较挑剔了,需要根据天时地利人和来选择,慎重哦!
1.4 马氏距离损失(Mahalanobis Distance Loss)
概念:
考虑特征之间的协方差,衡量样本之间的马氏距离。
马氏距离实际上是欧式距离在多变量下的“加强版”,用于测量点(向量)与分布之间的距离。
用法:
适用于高维空间中的聚类或分类问题
1.5 哈林顿距离损失(Hamming Loss)
概念:
用于度量两个向量之间的相似性,通常用于多标签分类任务,衡量两个向量对应元素不相等的比率。
用法:
- 度量分类变量之间的距离
- 数据通过计算机网络传输时的错误纠正/检测。它可以用来确定二进制字中distorted bit的数目,作为估计误差的一种方法。
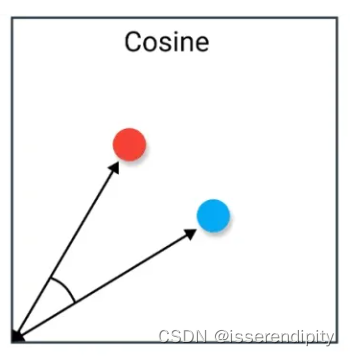
1.6 余弦相似度损失(Cosine Similarity Loss)
概念:
衡量模型输出值与真实值之间的余弦相似度
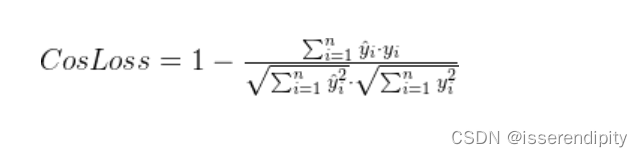
用法:
只考虑方向,没考虑大小。所以当大小不重要的时候,就可以用它了。
1.7 Jaccard 距离损失(Jaccard Distance Loss)
概念:
用于度量集合之间的相似性,通常用于聚类或分类问题。
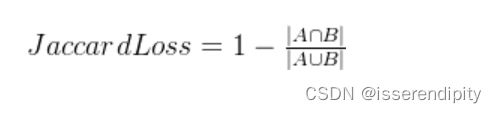
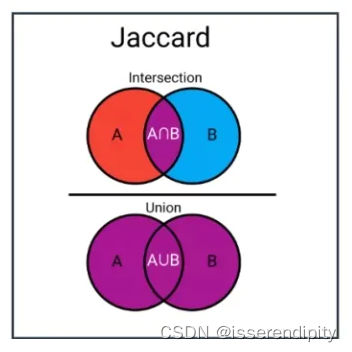
用法:
这个受数据集大小影响很大,当数据集很大时,他的交集和并集都会变大,损失值会很小就不准了。
经常用于处理二进制或者二进制化数据的应用程序中。例如预测衣服图像的片段时,Jaccard 索引就可以计算给出真实标签的预测片段的准确性。
还可以用来比较模式集,用于文本相似度分析,衡量文档之间的选词重叠程度。
这边介绍了基础的损失函数,下面还会介绍一些回归和分类中的损失函数。






















 2606
2606

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








