排序算法之插入排序

一  前言

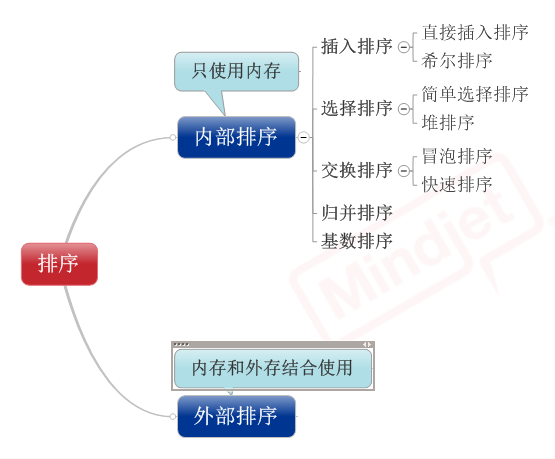
八种排序算法的关系：

二  插入排序

插入排序基本思想：按照关键字的大小将一个关键字插入到一个有序序列的文件的适当位置，并且使插入后的文件仍然是有序的。在插入的时候，寻找合适的位置可以采用顺序查找法，折半查找法等其他方法，相应的插入排序有：直接插入排序，折半插入排序，希尔排序。

结点定义：

template<class T>
class node
{
	friend class list < T >;
public:
	node():index(0){}
	~node(){}
	T getdata()
	{
		return data;
	}
private:
	T data;
};

表定义：

template<class T>
class list
{
	template<class T>
	friend  std::ostream& operator<<(std::ostream& out, list<T>& lst);
public:
	list() :maxsize(0), currsize(0){}
	list(int ms) :maxsize(ms)  //产生一序列数
	{
		vec = new node < T >[maxsize];
		std::cout << "please input" << maxsize << " numbers" << std::endl;
	//	vec[maxsize] = {0};
		T num;
		int i = 0;
		while (cin >> num)
		{
			if (i < maxsize)
			{
				vec[i].data = num;
				++i;
				++currsize;
			}
		}
	}
	~list()
	{
		delete[] vec;
		
	}

public:
	void Insertsort();
	void Binarysort();
	void Shellsort();
	
private:
	node<T>* vec;
	int maxsize;
	int currsize;
};

1.直接插入排序

基本思想：当插入第n个（n>1)个对象时候，假设前面(n-1) 个对象已经是排好顺序的，现在要把第n个数插到前面的有序数中，用第n个对象的关键值与第n-1,n-2...的顺序逐一进行比较，直至找到插入的位置插入。

核心：找位置，看过一篇博客说把找位置比喻成“找坑”，找到一个比自己大的数，就用那个位置的土把自己前面一个的坑给填上，直至遇到比自己小的 数（循环结束），用要插入的值把最合适的坑填上。

方法一：

template<class T>
void list<T>::Insertsort()     //直接排序法
{
	int j,k;
	for (int i = 1; i < currsize; ++i)
	{
		for (j = i - 1; j >= 0; --j)  //与前n-1个数中相比较，找到插入位置
			if (vec[i].data >= vec[j].data) //找到位置
				break;

		if (j != i - 1)  //找到插入位置后，就要移动数据；如果j==i-1，就不需要移动数据
		{
			node<T>* temp=new node<T>;
			temp->data= vec[i].data;
			for (k = i-1; k>j; --k)
				vec[k+1].data = vec[k].data;

			vec[k+1].data= temp->data; //插入数据
			delete temp;
			temp = nullptr;

		}
	}
}

方法二：

template<class T>
void list<T>::Insertsort()     //直接排序法
{
	for (int i = 1; i < currsize; ++i) //排序
	{
		node<T> temp = vec[i];
		int j = i;
		while (j>0 && (temp.data < vec[j - 1].data))  //找到要插入的位置
		{
			vec[j].data = vec[j - 1].data;
			--j;
		}
		vec[j].data = temp.data;
	}
}

2.折半插入排序

基本思想：当插入第n个（n>1)个对象时候，假设前面(n-1) 个对象已经是排好顺序的，现在要把第n个数插到前面的有序数中，利用”折半查找法“来查找插入的位置。

template<class T>
void list<T>::Binarysort()     //折半插入排序法
{
	for (int i = 1; i < currsize; ++i)
	{
		int left = 0; int right = i - 1;   
		node<T>* temp = new node < T > ;
		 temp->data=vec[i].data;
		int j = i;
		while (left <= right) //找到插入位置
		{
			int middle = (left + right) / 2;
			if (temp->data < vec[middle].data)
				right = middle - 1;
			else
				left = middle + 1;
		}
      
		for (int k = i - 1; k >= left; --k) //移动数据
			vec[k + 1].data = vec[k].data;
		vec[left].data = temp->data;
		delete temp;
		temp = nullptr;
	}
}

3.希尔排序

基本思想：不断的把待排序的一组数据按间隔值分成若干小组，然后对同一组的数据进行排序。

基本操作：设待排序列有n个对象，首先取一个整数gap作为间隔，将全部序列分成gap个子序列，所有距离为gap的对象放在同一个子序列中，每个子序列分别进行直接插入排序，然后逐渐缩小gap，直至gap=1.将所有的序列放入同一组中。

template<class T>
void list<T>::Shellsort()   //希尔排序
{
	int gap = currsize / 2;
	while (gap)    //循环到间隔gap=0
	{
		for (int i = gap; i < currsize; ++i)    //对各个子序列进行排序
		{
			node<T> temp;
			temp.data = vec[i].data;
			int j = i;
			while (j >= gap&&temp.data < vec[j - gap].data) //与前面一个元素进行比较
			{
				vec[j].data = vec[j - gap].data;
				j = j - gap;
			}
			vec[j].data = temp.data;
		}
		if (gap == 2) //当间隔为2的排序结束后，将gap=1
		{
			gap = 1;
		}
		else
		{
			gap = (int)gap / 2.2;
		}
	}
}

补充： Java版本

// 直接插入排序法
  public int[] insertSort(int[] arr){
	  int size = arr.length;
	  int i = 0, j = 0;
	  if(size > 0){
		  for(i = 1;i < size;++i){
			  if(arr[i - 1] > arr[i]){
				  int temp = arr[i];   // 保存较小的值
				  // 对前 i-1 个数再进行排序
				  for(j = i-1; j >= 0 && arr[j] >= temp; --j){
					  arr[j+1] = arr[j];
				  }
				  arr[j+1] = temp;
			  }
		  }
	  }
	  return arr;
  }
  
  // 折半插入排序法
  public int[] binarySort(int[] arr){
	  int size = arr.length;
	  if(size > 0){
		  // 想插入第n个数，假设前n-1个为有序的
		  for(int i = 1; i < size ; ++i){
			  int left = 0, right = i - 1;
			  //要插入的数
			  int temp = arr[i];
			  // 寻找插入的位置
			  while(right >= left){
				  int mid = (right + left)/2;
				  if(arr[mid] > arr[i])
					  right = mid - 1;
				  else
					  left = mid + 1;
			  }
			  // 移动数据
			  for(int k = i;k > left; --k){
				  arr[k] = arr[k-1];
			  }
			  arr[left]=temp;
		  }
	  }
	  return arr;
  }
  
  // 希尔排序
  public int[] shellSort(int[] arr){
	  // 希尔排序就是根据间隔gap将序列分成几组分别利用直接插入排序法排序，直至gap为1
	  int size = arr.length;
	  int gap = size/2; // 初始gap
	  while(gap >= 1){
		  for(int i = gap; i < size; ++i){
			  int temp = arr[i];
			  int  j = 0;
			  for(j = i; j >= gap && arr[j - gap] > temp; j=j-gap){
				  arr[j] = arr[j-gap]; 
		      }
			  arr[j] = temp;
		  }
		  if(gap == 2){
			  gap = 1;
		  } else {
			  gap = (int) (gap / 2.2);
		  }
	  }
	  return arr;
  }