机器学习之logistic回归的梯度上升算法

机器学习之logistic回归的梯度上升算法

算法背景：

一般来说，回归模型一般不用在分类问题上，因为回归是连续型模型，而且受噪声的因素很大，但是，若需要选择，可以选择使用logisti 回归。

对数回归本质上是线性回归，只是在特征到结果的映射里加入了一层函数映射，选择g(z)=1/(1+exp（-z）)作为sigmoid函数进行映射，可以将连续值映射到0-1之间。

其中g(z)函数的图像如下：可以看到，函数的取值始终在0-1之间。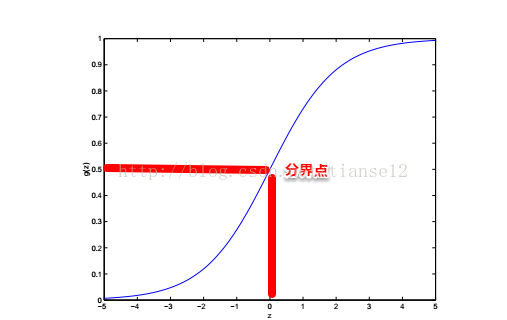

对于分类问题，我们可以建立假设：

          if（z >= 0.5） g(z)=1;  if（z < 0.5） g(z)=0;

算法思想：

对于输出值为y={0,1}的两类分类问题，我们做出一个假设

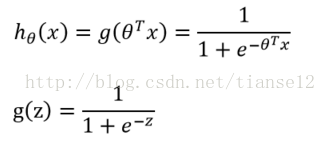
函数g(z)即为上文提到的sigmoid函数，其导数形式为：

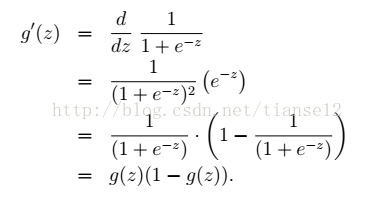
根据这个函数，我们可以得到对于一个样本的概率分布为：

综合起来就是：

现在就可以将问题转化为求Logistic回归的最佳系数，因为logistic回归可以被看做一种概率模型，且y发生的概率与回归参数Θ有关，因此我们可以对Θ进行最大似然估计，使得y发生的概率最大，此时的Θ 便是最优回归系数：

对数据集求似然函数，并取对数计算：

要使得最大化，则运用梯度上升法，求出最高点：

计算结果为：

此公式便是梯度上升算法的更新规则，α是学习率，决定了梯度上升的快慢。可以看到与线性回归类似，只是增加了特征到结果的映射函数。

代码实现python：

#coding=utf-8
#logistic回归的梯度上升法

from numpy import *
import matplotlib.pyplot as plt
#加载数据集
def loadDataSet():
    dataMat = [];
    labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])#x0=1
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inx):
    return 1.0 / (1 + exp(-inx));

#梯度上升，主要是采用了最大似然的推导
def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m, n = shape(dataMatrix)#n=3
    alpha = 0.001#学习率
    maxCycles = 500#循环轮数
    theta = ones((n, 1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * theta)
        error = (labelMat - h)
        theta = theta + alpha * dataMatrix.transpose() * error
    return theta
#根据训练好的theta绘图
def plotBestFit(theta):
    dataMat,labelMat = loadDataSet()
    dataArr =array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    #将数据按真实标签进行分类
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    ax.scatter(xcord1, ycord1, s = 30, c = 'red', marker='s')
    ax.scatter(xcord2, ycord2, s = 30, c = 'blue')
    #生成x的取值 -3.0——3.0,增量为0.1
    x = arange(-3.0, 3.0, 0.1)
    #y = Θ0+Θ1x1+Θ2x2
    #y=x2
    y = (-theta[0] - theta[1] * x) / theta[2]
    ax.plot(x, y.T)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()
dataMat,labelMat = loadDataSet()#加载数据集
theta = gradAscent(dataMat,labelMat)#计算参数
plotBestFit(theta)#根据参数画出分界线以及相应分类点

结果演示：