（EM算法）The EM Algorithm_em算法课本-CSDN博客

（EM算法）The EM Algorithm

EM是我一直想深入学习的算法之一，第一次听说是在NLP课中的HMM那一节，为了解决HMM的参数估计问题，使用了EM算法。在之后的MT中的词对齐中也用到了。在Mitchell的书中也提到EM可以用于贝叶斯网络中。

下面主要介绍EM的整个推导过程。

1. Jensen不等式

回顾优化理论中的一些概念。设f是定义域为实数的函数，如果对于所有的实数x，，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的（），那么f是凸函数。如果或者，那么称f是严格凸函数。

Jensen不等式表述如下：

如果f是凸函数，X是随机变量，那么

特别地，如果f是严格凸函数，那么当且仅当，也就是说X是常量。

这里我们将简写为。

如果用图表示会很清晰：

图中，实线f是凸函数，X是随机变量，有0.5的概率是a，有0.5的概率是b。（就像掷硬币一样）。X的期望值就是a和b的中值了，图中可以看到成立。

当f是（严格）凹函数当且仅当-f是（严格）凸函数。

Jensen不等式应用于凹函数时，不等号方向反向，也就是。

2. EM算法

给定的训练样本是，样例间独立，我们想找到每个样例隐含的类别z，能使得p(x,z)最大。p(x,z)的最大似然估计如下：

第一步是对极大似然取对数，第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求一般比较困难，因为有隐藏变量z存在，但是一般确定了z后，求解就容易了。

EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化，我们可以不断地建立的下界（E步），然后优化下界（M步）。这句话比较抽象，看下面的。

对于每一个样例i，让表示该样例隐含变量z的某种分布，满足的条件是。（如果z是连续性的，那么是概率密度函数，需要将求和符号换做积分符号）。比如要将班上学生聚类，假设隐藏变量z是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了。

可以由前面阐述的内容得到下面的公式：

（1）到（2）比较直接，就是分子分母同乘以一个相等的函数。（2）到（3）利用了Jensen不等式，考虑到是凹函数（二阶导数小于0），而且

就是的期望（回想期望公式中的Lazy Statistician规则）

设Y是随机变量X的函数（g是连续函数），那么

（1） X是离散型随机变量，它的分布律为，k=1,2,…。若绝对收敛，则有

（2） X是连续型随机变量，它的概率密度为，若绝对收敛，则有

对应于上述问题，Y是，X是，是，g是到的映射。这样解释了式子（2）中的期望，再根据凹函数时的Jensen不等式：

可以得到（3）。

这个过程可以看作是对求了下界。对于的选择，有多种可能，那种更好的？假设已经给定，那么的值就决定于和了。我们可以通过调整这两个概率使下界不断上升，以逼近的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明我们调整后的概率能够等价于了。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到：

c为常数，不依赖于。对此式子做进一步推导，我们知道，那么也就有，（多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c），那么有下式：

至此，我们推出了在固定其他参数后，的计算公式就是后验概率，解决了如何选择的问题。这一步就是E步，建立的下界。接下来的M步，就是在给定后，调整，去极大化的下界（在固定后，下界还可以调整的更大）。那么一般的EM算法的步骤如下：

循环重复直到收敛 {

（E步）对于每一个i，计算

（M步）计算

那么究竟怎么确保EM收敛？假定和是EM第t次和t+1次迭代后的结果。如果我们证明了，也就是说极大似然估计单调增加，那么最终我们会到达最大似然估计的最大值。下面来证明，选定后，我们得到E步

这一步保证了在给定时，Jensen不等式中的等式成立，也就是

然后进行M步，固定，并将视作变量，对上面的求导后，得到，这样经过一些推导会有以下式子成立：

解释第（4）步，得到时，只是最大化，也就是的下界，而没有使等式成立，等式成立只有是在固定，并按E步得到时才能成立。

况且根据我们前面得到的下式，对于所有的和都成立

第（5）步利用了M步的定义，M步就是将调整到，使得下界最大化。因此（5）成立，（6）是之前的等式结果。

这样就证明了会单调增加。一种收敛方法是不再变化，还有一种就是变化幅度很小。

再次解释一下（4）、（5）、（6）。首先（4）对所有的参数都满足，而其等式成立条件只是在固定，并调整好Q时成立，而第（4）步只是固定Q，调整，不能保证等式一定成立。（4）到（5）就是M步的定义，（5）到（6）是前面E步所保证等式成立条件。也就是说E步会将下界拉到与一个特定值（这里）一样的高度，而此时发现下界仍然可以上升，因此经过M步后，下界又被拉升，但达不到与另外一个特定值一样的高度，之后E步又将下界拉到与这个特定值一样的高度，重复下去，直到最大值。

如果我们定义

从前面的推导中我们知道，EM可以看作是J的坐标上升法，E步固定，优化，M步固定优化。

3. 重新审视混合高斯模型

我们已经知道了EM的精髓和推导过程，再次审视一下混合高斯模型。之前提到的混合高斯模型的参数和计算公式都是根据很多假定得出的，有些没有说明来由。为了简单，这里在M步只给出和的推导方法。

E步很简单，按照一般EM公式得到：

简单解释就是每个样例i的隐含类别为j的概率可以通过后验概率计算得到。

在M步中，我们需要在固定后最大化最大似然估计，也就是

这是将的k种情况展开后的样子，未知参数和。

固定和，对求导得

等于0时，得到

这就是我们之前模型中的的更新公式。

然后推导的更新公式。看之前得到的

在和确定后，分子上面的一串都是常数了，实际上需要优化的公式是：

需要知道的是，还需要满足一定的约束条件就是。

这个优化问题我们很熟悉了，直接构造拉格朗日乘子。

还有一点就是，但这一点会在得到的公式里自动满足。

求导得，

等于0，得到

也就是说再次使用，得到

这样就神奇地得到了。

那么就顺势得到M步中的更新公式：

的推导也类似，不过稍微复杂一些，毕竟是矩阵。结果在之前的混合高斯模型中已经给出。

4. 总结

如果将样本看作观察值，潜在类别看作是隐藏变量，那么聚类问题也就是参数估计问题，只不过聚类问题中参数分为隐含类别变量和其他参数，这犹如在x-y坐标系中找一个曲线的极值，然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了。但固定一个变量后，另外一个可以通过求导得到，因此可以使用坐标上升法，一次固定一个变量，对另外的求极值，最后逐步逼近极值。对应到EM上，E步估计隐含变量，M步估计其他参数，交替将极值推向最大。EM中还有“硬”指定和“软”指定的概念，“软”指定看似更为合理，但计算量要大，“硬”指定在某些场合如K-means中更为实用（要是保持一个样本点到其他所有中心的概率，就会很麻烦）。

另外，EM的收敛性证明方法确实很牛，能够利用log的凹函数性质，还能够想到利用创造下界，拉平函数下界，优化下界的方法来逐步逼近极大值。而且每一步迭代都能保证是单调的。最重要的是证明的数学公式非常精妙，硬是分子分母都乘以z的概率变成期望来套上Jensen不等式，前人都是怎么想到的。

在Mitchell的Machine Learning书中也举了一个EM应用的例子，明白地说就是将班上学生的身高都放在一起，要求聚成两个类。这些身高可以看作是男生身高的高斯分布和女生身高的高斯分布组成。因此变成了如何估计每个样例是男生还是女生，然后在确定男女生情况下，如何估计均值和方差，里面也给出了公式，有兴趣可以参考。

标签: Machine Learning

绿色通道：好文要顶关注我收藏该文与我联系

JerryLead
关注 - 4
粉丝 - 1227

+加关注

(请您对文章做出评价)

« 上一篇：混合高斯模型（Mixtures of Gaussians）和EM算法
» 下一篇：在线学习（Online Learning）

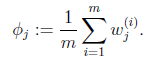
posted on 2011-04-06 16:18 JerryLead 阅读(94631) 评论(48) 编辑收藏

#1楼  2011-04-06 16:45joelike

作者太好了！顶顶顶！

支持(0) 反对(0)

#2楼  2011-05-22 17:56LeftNotEasy

支持一下，文章写得很好，而且公式很漂亮，请问楼主公式是怎么弄上去的呢

支持(0) 反对(0)

#3楼 [楼主] 2011-05-24 16:46JerryLead

@LeftNotEasy
呵呵，得到了大牛的认可，比较模糊的公式是从讲义上截图截下来的，稍微清晰点就是word的公式编辑器。看到Leo Zhang的用Latex的公式更加漂亮，打算有空学学。

支持(0) 反对(0)

#4楼  2011-05-24 16:52LeftNotEasy

@JerryLead
大牛不敢当，我也涉及这个领域时间很短，呵呵，以后多多讨论：）

支持(0) 反对(0)

#5楼  2011-05-31 22:48耒子之心

楼主好文，看了之后的对EM的了解加深了。

支持(0) 反对(0)

#6楼  2011-07-24 21:41emanlee

图中，实线f是凸函数--好似凹函数？

支持(0) 反对(0)

#7楼  2011-07-26 12:13goolee[未注册用户]

凹凸是看有沒有CONVEX決定...

#8楼  2011-07-29 18:29mirth[未注册用户]

抄袭之作
www.seanborman.com/publications/EM_algorithm.pdf

#9楼 [楼主] 2011-07-29 20:19JerryLead

@mirth
你看的很仔细，如果你看的再仔细一点话，或者看了前面或后面的文章就会发现，这里的大部分文章内容都来自于Stanford的ML课程讲义（当然我在前面或者后面的文章都提到了，当然也有来自其他论文的内容，当然也有我自己的认识和理解的内容。
你给的链接也是tutorial，也算是抄袭别人的论文，但这些东西又不是拿去发表或者赚钱。另外，blog的内容其实都很随意。如果你认为我抄袭了你的东西或者我拿别人的东西去发表了，欢迎指出。

支持(10) 反对(0)

#10楼  2011-08-15 11:14wchaor[未注册用户]

你好，你的文章对我帮助很大。请问你能否把文章中的原始文献发给我呢？非常感谢！

#11楼 [楼主] 2011-08-21 21:41JerryLead

@wchaor
请google "stanford em algorithm"第一个或 http://www.stanford.edu/class/cs229/notes/

支持(0) 反对(0)

#12楼  2011-09-01 11:51求答[未注册用户]

p(zi|xi;θ)怎么求

#13楼 [楼主] 2011-09-01 15:27JerryLead

@求答
请看这一篇《混合高斯模型（Mixtures of Gaussians）和EM算法》，不同的模型有不同的p(zi|xi;θ)

支持(0) 反对(0)

#14楼  2011-10-31 14:12huangshujia

@JerryLead
楼主，你的个性我欣赏！！呵呵！

支持(0) 反对(0)

#15楼  2011-12-02 19:41chinabing

楼主翻译的很好，有些地方加了一些注释，易懂，很好。

支持(0) 反对(0)

#16楼  2011-12-19 00:08asdffdas

自己看CS229，感觉还是不太好理解，博主的翻译很能帮助理解

支持(0) 反对(0)

#17楼  2012-01-02 15:45bmfire[未注册用户]

函数的凸凹性弄错了吧

#18楼  2012-01-13 14:21flyf[未注册用户]

写的很好，加入了自己的理解。请教一个问题，在确保EM收敛时，做法是在M步使其单调递增保证收敛。隐含的条件是函数有界，有界是如何理解呢？多谢。

#19楼 [楼主] 2012-01-28 11:06JerryLead

@bmfire
这里的凸凹性翻译自原文，convex我翻译为凸，concave为凹。与我们在高数里面学的有点不一样，高数里正好相反，凹凸性在优化理论里又不太一样，这里我终于原文了。

支持(0) 反对(0)

#20楼 [楼主] 2012-01-28 12:37JerryLead

@flyf
我对这个问题理解不深，谈谈感觉吧。感觉这个不仅仅是EM算法的问题了，是一般优化问题是否有极值、最大值、最小值的问题了。这里M步的优化函数是连续的，固定Qi(z^(i))后，就变成求log(p(x^(i),z^(i);theta)的极大值了，log是凹函数，有极大值。

支持(0) 反对(0)

#21楼  2012-04-07 13:59南窗

JerryLead，你好
请问你是如何理解EM最大似然估计中的θ，模型中似乎没有明确指明θ的意义

支持(0) 反对(0)

#22楼  2012-04-18 13:17duanchw37

讲的的太好了，我感觉EM方法更像是一种思路，遇到不同的问题有不同的处理。真的遇到实际问题的时候还是很乱，继续学习。。。

支持(0) 反对(0)

#23楼  2012-05-03 19:56duguyixiaono1

太感谢博主了，哥终于看懂了！！！！！卧槽。。。。谢谢博主！！！！！

支持(0) 反对(0)

#24楼  2012-06-15 17:30conspicuous

EM算法太重要了，楼主威武，我看了英文视频都没看明白楼主一点就透了

支持(0) 反对(0)

#25楼  2012-11-23 16:28CanaanShen

mark~

支持(0) 反对(0)

#26楼  2012-12-13 22:32liyitan

看了楼主的讲解收益匪浅，但是还是有一个问题，就是楼主说梯度下降方法就不适用的原因是不能求导，貌似不太对吧，只要形式可以就可以求导，只不过没有解析解，没有解析解不意味着不能用梯度下降法吧？

支持(0) 反对(0)

#27楼  2013-07-15 17:22tianyanfl

Jensen不等式里的那个函数图画错了！那是凹函数，里面的标记也完全记了！抄的也不好好看看~！！

支持(0) 反对(0)

#28楼  2013-11-10 20:17zss19910423

卧槽，楼主，我真的忍不住了，只有这俩个字才能代表我此刻看完的心情呀。俺老师上课给我们讲解这个，推着推着然后就推倒不下去了，让我们自己推导，，，，看到这个我终于得到解说了

支持(0) 反对(0)

#29楼  2013-12-06 16:48林羽飞扬

谢谢博主的精彩译文，终于明白了EM算法

支持(0) 反对(0)

#30楼  2013-12-12 21:37痞子寇

收敛性的证明看不懂，望能指教，整体思路很清晰，就是收敛性证明过度的太快。谢谢指教！

支持(0) 反对(0)

#31楼  2014-01-14 12:49sunjunli

关于统计学习的问题.我认为人监督情况下,有足够的统计,模型就会越来越好.在者,已经有一个好的模型,在此基础上,继续融入统计,模型将变得更加丰富.我的邮箱sunjunlishi@163.com,你的邮箱多少?

支持(0) 反对(0)

#32楼  2014-02-20 22:46cc_jony

智商捉急啊表示没看懂

支持(0) 反对(0)

#33楼  2014-03-07 14:10元子@speed

确实写得太好了，原来一窍不通，看完这篇，不懂，于是看上一篇，混合高斯模型，朦朦胧胧了，再看上一篇，Kmeans角度来理解EM，瞬间恍然大悟了，原来Kmeans的深层意思是这么理解的！！EM也就易懂了

支持(0) 反对(0)

#34楼  2014-04-17 14:58欣然未央

谢谢，真的写得很好，课本上就是讲了一个大概，没有具体的推到，没有具体的原理就是一个硬板帮的公式，真实太好了。必须顶

支持(0) 反对(0)

#35楼  2014-04-18 21:57折花饮酒

这个结合cs229讲义，真棒

支持(0) 反对(0)

#36楼  2014-07-04 16:30ziranjuan

@mirth

我倒是期待您多少抄一些有用的东西与大家分享，而不是在这里指摘付出辛勤劳动的博主，没有冒犯之意，请见谅！

支持(1) 反对(0)

#37楼  2014-07-15 10:07chq

讲的很不错，谢谢了。公式 4 5 6 顺序改为 6 5 4 更好。6到5是E步骤即在给定θ下，求隐藏变量Qi，等式成立。5到4为M步即已知隐藏变量Qi求θ的最大似然估计。

支持(0) 反对(0)

#38楼  2014-07-23 15:57Transposition

@JerryLead
楼主是用Word的公式编辑器写，然后用Word发布的吗？

支持(0) 反对(0)

#39楼  2014-08-11 14:32MissBoy

在证明可以收敛的时候，为什么选定Q(t,z)后就使jesen不等式的等式成立了呢？这不应该只是jesen不等式等式成立的必要条件吗？求博主或看懂的人指点

支持(0) 反对(0)

#40楼  2014-10-14 10:51keyalone

@MissBoy
先解释第一个问号吧！首先是Q(z(i);theta),在参数theta不变的情况下，当选定Q时，能使p(x(i),z(i);theta)/Q(z(i);theta) 为常数的概率为1.即等式成立。如果你理解jensen inequality的话，这个就是正确的。第二个问题
要想使不等式中的等式成立Q必须取这个值，当Q取这个值时，等式就成立，这个与jensen不等式的成立没有关系，即使Q为任意值，这个不等式就成立，但是有个特殊情况，那就是当Q为上面说的特殊值时，等式成立，也就是下界最大的情况。由于符号复杂，就没有书写符号了

支持(0) 反对(0)

#41楼  2014-11-06 16:58siluwb

最近也在看斯坦福的机器学习公开课，博主的文章大部分内容与之相似。但毕竟翻译成中文也是一个大工程，且没有遗漏，很多细节有自己的理解，非常棒。赞一个

支持(0) 反对(0)

#42楼  2014-12-22 20:38xx ee

问一个比较浅的问题：在4. 总结中，有 “然而曲线函数不能直接求导，因此什么梯度下降方法就不适用了----”为啥曲线不能求导？

支持(0) 反对(0)

#43楼  2015-02-01 21:47扭定乾坤

博主，太强了，看完，直接秒懂！！！

支持(0) 反对(0)

#44楼  2015-02-02 11:24读博好痛苦

建议博主给出原文的引用链接，至少也应该把原文的作者写出来

支持(0) 反对(0)

#45楼  2015-03-17 11:02牛虻07

Jensen不等式表述如下：
一直到下面的那幅图这一段
问一下：
在这一段的表达中，有E[f(X)]>=f[E(X)]，但下面的图中，f(a)与f(b)连线的中点，是E[f(X)]吗？E[f(x)]=积分(p(x)*f(x))不应该是这样吗？

但E[f(x)]=积分(p(x)*f(x))不等于1/2[f(a)+f(b)]吧。

支持(0) 反对(0)

#46楼  2015-03-29 21:43木幽落_思

博主好，首先非常感谢分享文章，收货颇丰，有一点疑惑希望给予解答，在“多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是c”这里，认为常数C与Z(i)无关是常数，我疑惑的是对每一个Z(i)来说，P(X(i),Z(i)；theta)/Q(Z(i)都是一样的吗，这里麻烦说明下，或者给点资料，Thank You！

支持(1) 反对(0)