Matlab linprog函数：手把手教你解线性规划问题

最新推荐文章于 2025-09-23 16:10:26 发布

原创最新推荐文章于 2025-09-23 16:10:26 发布 · 1k 阅读

38 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #机器学习 #算法

数学建模专栏收录该内容

11 篇文章

订阅专栏

文章目录

一、先搞懂：linprog是干嘛的？

简单说，linprog 是 Matlab 里专门用来解“线性规划”的工具。啥是线性规划？比如“生产多少产品能让利润最大”“用多少原料能让成本最低”——只要目标（利润/成本）和约束（原料限制/产量限制）都是“线性的”（比如 x1 + 2x2 ≤ 10 这种一次式），都能用它解决。

它的核心调用格式就一句话：
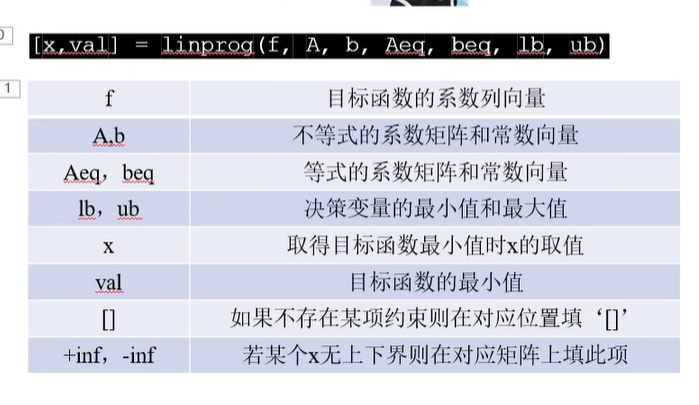
[x, val] = linprog(f, A, b, [], [], lb, ub)

先简单说下输出和输入是啥（后面逐个拆解开讲）：

输出：
- x：最终找到的“最优解”（比如生产x1=多少、x2=多少）；
- val：对应最优解的“目标函数最小值”（如果要最大化，后面要简单处理下，别急）。
输入：一堆和“目标函数”“约束条件”相关的参数，咱们一个个说。

先看个完整样例，有个整体印象：

二、逐个拆讲：每个参数到底填啥？

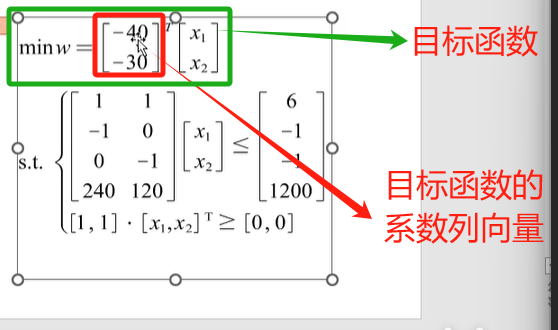
1. f：目标函数的“系数向量”

f 是目标函数里，每个决策变量（比如x1、x2）前面的系数，注意：linprog默认求“目标函数的最小值”。如果你的问题是“求最大值”（比如最大利润），就得把系数改成负数，转成“求最小值”问题。

举个例子：
如果原问题是“最大化利润 = 40x1 + 30x2”，那转成linprog能处理的“最小化问题”就是“最小化 -40x1 -30x2”，所以 f 就是这两个系数组成的向量：

f = [-40; -30];  % 分号表示列向量，x1系数-40，x2系数-30

对应到目标函数的结构，看这张图更清楚：

2. A、b：不等式约束的“系数矩阵”和“常数项”

这俩是一对，用来描述“线性不等式约束”（比如 x1 - x2 ≤ 6、240x1 + 120x2 ≤ 1200）。记住一个规则：linprog默认约束是 “A*x ≤ b”（A乘以x小于等于b），所以要把所有不等式都整理成这种形式。

怎么填A和b？

A：每行对应一个不等式的“变量系数”，列数和决策变量个数一致（比如x1、x2就是2列）；
b：每一行对应一个不等式右边的“常数项”，是个列向量。

看例子里的约束条件和A、b的对应关系：
假设约束是这4个：

x1 - x2 ≤ 6
-x1 + 0x2 ≤ -1（可理解为x1 ≥ 1）
0x1 - x2 ≤ -1（可理解为x2 ≥ 1）
240x1 + 120x2 ≤ 1200

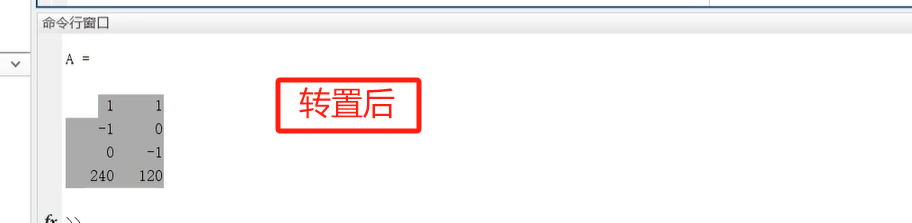
那A就是这4个约束的“变量系数”组成的矩阵，注意要转置（因为原写法是行向量，Matlab里需要列向量转成矩阵行）：

A = [1,-1,0,240; 1,0,-1,120]';  % 转置符号'不能漏！转置后A是4行2列

b就是这4个约束右边的常数，组成列向量：

b = [6; -1; -1; 1200];  % 4个常数，对应4个约束

看这张图，能直观看到约束和A、b的对应：

再看A转置后的结构（每行对应一个约束的系数）：

b和约束的对应更直接，看这张：

最后确认A*x ≤ b的整体逻辑：

3. 中间两个[]：没有等式约束就填空

调用格式里，A和b后面有两个空的[]，这俩位置是留给“等式约束”（比如 x1 + x2 = 5）的参数Aeq和Beq的。如果你的问题里没有等式约束（大部分简单问题都没有），就直接填[]，不用写任何东西。

比如例子里没有等式约束，所以写成 [], []。

4. lb、ub：决策变量的“上下限”

lb（lower bound）是每个决策变量的“最小值”，ub（upper bound）是“最大值”，都是列向量，个数和决策变量一致（x1、x2就是2个元素）。

举个例子：
如果x1和x2都是“非负”的（比如生产数量不能是负数），且没有最大限制（可以无限多生产），那：

lb = [0; 0];        % x1≥0，x2≥0（最小值都是0）
ub = [+inf; +inf];  % x1、x2无上限（inf是Matlab里的“无穷大”）

如果有上限（比如x1最多生产10），就把ub改成 [10; +inf] 就行。

三、结果怎么看？val到底是啥？

运行 [x, val] = linprog(...) 后，会得到两个结果：

x：比如x=[2;4]，意思是“当x1=2、x2=4时，满足所有约束”；
val：这是linprog算出来的“目标函数最小值”。

这里要注意：如果之前为了“求最大值”把f的系数取了负（比如原目标是最大化40x1+30x2，f用了[-40;-30]），那val会是负数，实际的最大值就是val的相反数（比如val=-200，那最大利润就是200）。

四、所有参数一图览：记不住就看这个

最后放一张参数位置总结图，下次写代码时对着填就行，不用记顺序：

总结：用linprog的3个步骤

把问题整理成“线性规划”形式：明确目标函数（最大化转最小化，改f的符号）、不等式约束（整理成A*x ≤ b）、变量上下限；
按顺序填参数：f → A、b → 两个[]（无等式约束）→ lb、ub；
运行函数，看x（最优解）和val（目标最小值），需要最大值就取val的相反数。

按这个流程走，不管是求最大利润还是最小成本，都能轻松搞定～