关于NSGA-II的算法学习

最新推荐文章于 2025-03-11 20:33:08 发布

吴铭星

最新推荐文章于 2025-03-11 20:33:08 发布

阅读量2.6k

点赞数 6

文章标签：算法

本文链接：https://blog.csdn.net/whu_wmx/article/details/130698188

版权

NSGA-II是一种用于多目标优化问题的遗传算法，包括初始化、非支配排序、计算拥挤度、选择、交叉和变异等步骤。通过非支配关系和拥挤度计算，算法能找出多个最优解的帕累托前沿。Python实现的代码可帮助理解算法流程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

因为最近要求整理一个博客，把这些月的工作学习写一下

之后打算把这些文章迁移到我的博客上，先用这个来写一下

关于NSGA-II的算法，它全称为 Non-dominated Sorting Genetic Algorithm II，是一种广泛使用的多目标优化（Multi-Objective Optimization）遗传算法。这种算法由 K. Deb 等人在 2002 年提出，用于解决多目标优化问题。

当时对着论文看的时候很木，很呆，啃了很久，因为当时看的文献是解决实际问题的，文章对这个模型解释不是很清楚，于是去b站看了一个视频：

NSGA2多目标优化案例，保姆级教程，纯手打代码_哔哩哔哩_bilibili

其实这些视频大差不差，因为原理很简单，所以我选择了手打代码的，这样更清晰。当然这个是matlab实现的，我最后利用的是python。

接下来介绍一下原理，首先会按论文的方法写一下，然后按我自己的通俗理解写一下：

NSGA-II 算法的主要步骤如下：

初始化：首先，生成一个初始的解集合（也称为种群）。
非支配排序：将种群中的解按照非支配关系进行排序。非支配关系是指在所有目标函数上，一个解都不比另一个解差，这种解就被称为非支配解。排序后的解被分为若干个非支配等级。
计算拥挤度：在每个非支配等级内，计算每个解的拥挤度。拥挤度是衡量解周围空间拥挤程度的指标，计算方式是在目标空间中，计算每个解在各目标函数上的相邻解之间的距离。
选择：使用二元锦标赛选择法进行选择。在这种方法中，每次随机选择两个解，比较它们的非支配等级和拥挤度，选择非支配等级较小或拥挤度较大的解。
交叉和变异：使用交叉和变异操作生成新的解。这些操作模拟了生物进化中的遗传和突变过程。
更新种群：将新生成的解与当前种群合并，然后再次进行非支配排序和计算拥挤度，选择最优的解作为新的种群。
终止条件：如果满足终止条件（例如，达到最大迭代次数），则停止算法，否则返回步骤 4。

以下是流程图：

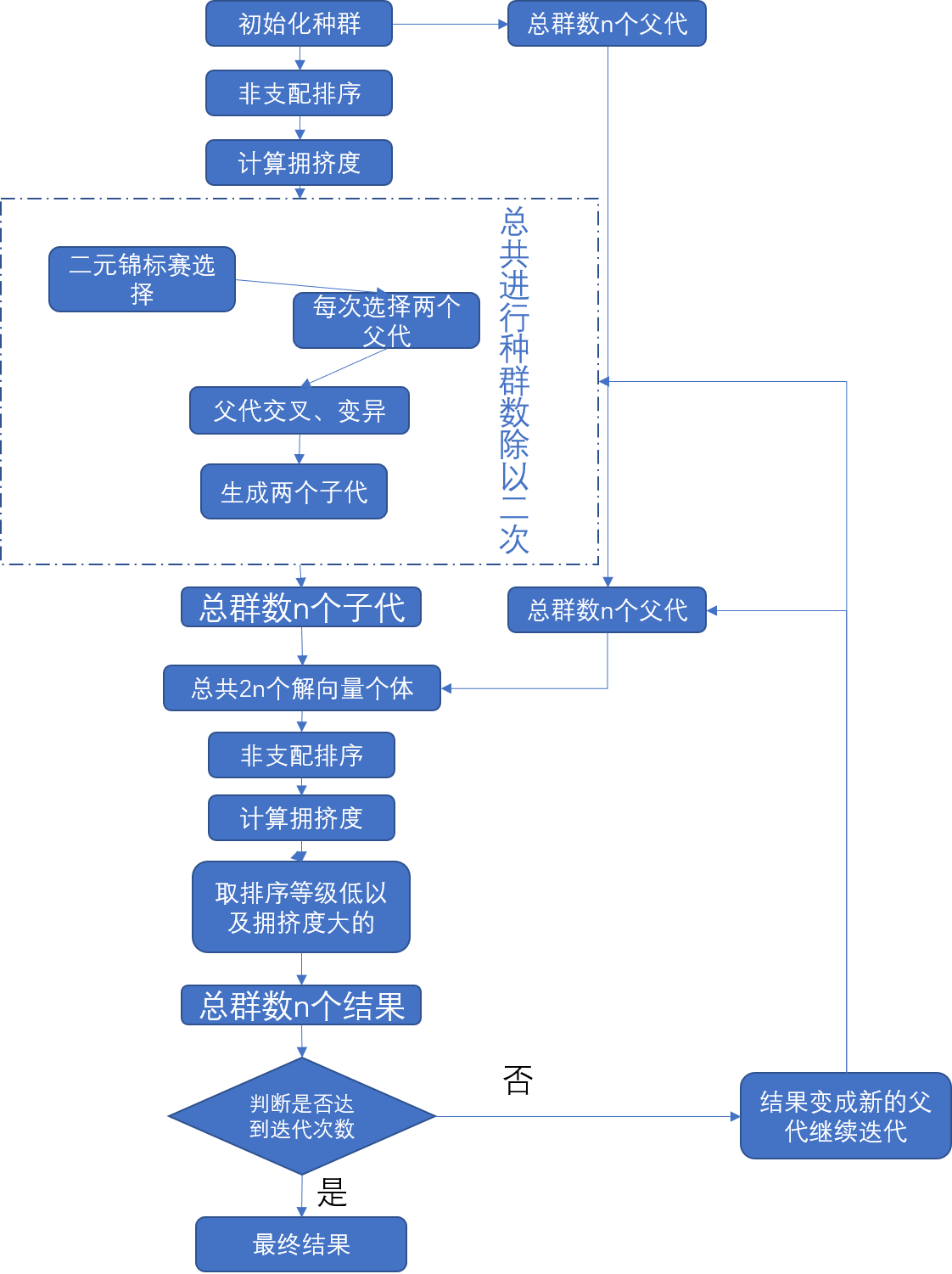
然后用通俗的我的大白话解释一下，这个NSGA-II我感觉核心的东西并不难，他首先定义了很多个解向量，什么是解向量呢，一组解向量相当于一种分配情况，向量相当于里面有很多个值，因为NSGA-II主要是解决多目标，比如说你可能问题有两个主要目标函数或者多个，拿具体的例子来说吧，如果是水资源分配，你可能水总量只有那么多，你要供给四个目标，你的水的来源有三个来源，那么最后的分配结果肯定是一个3X4的矩阵，那么这个一个解向量相当于维度是12，也就是说，它里面包含了具体怎么分配的12个值，比如说A水分配H地这种。

解释了解向量，我们再来看这个NSGA-II，他首先定义一个总群数，也就是一开始生成多少个解向量，然后对他们要判断，哪个是更好的，他们内部分个等级，也就是上面的“非支配排序”，可以说，低等级的，肯定是各方面完爆高等级的，炉石传说没有。。。跑题了。比如说，一个解向量，他的目标函数A的值和目标函数B的值都要好于第二个解向量，那么第一个解向量我们就认为它是低等级的。（当然，有的目标函数值在很多问题有着不一样的判定什么是优，比如说A值越大越好，B值越小越好，那么我们的第一个解向量当在A值大于第二个解向量同时B值小于第二个，我们就判断，前者支配后者，前者的等级低于后者）

然后我们只是分了等级，但是统一等级，这个算法也需要我们比个高低，所以就有了拥挤度计算，拥挤度一般是越远越好，因为容易交叉产生的结果比较更有随机性，这一方面可能大白话比较难解释，推荐去看b站上面的视频。总之，拥挤度是用来排序统一等级的。

经过上一轮排序，所有解向量，都有了各自的排名，此刻我们要增加一些变数，也就是交叉和变异，可以理解为，在这些个体（解向量中）首先随机选择两个，然后选择一个比较优秀的出来，然后再选择两个，比较出一个优秀的出来，然后就有两个选择出来还算优秀的父代，（当选择一样的父代的时候换一个），此刻交叉就是他们换几个解（因为是解向量嘛，中间换几个值）或者一些交叉的方式，然后随机选择他们里面的解在约束条件下乘以或者加一个随机数，这样可以生成两个新的解向量，一般也生成跟父代一样的个数，或者少一点应该也行。

此刻个体就来到了先前的两倍（子代加父代），然后对这群个体再排序，计算支配等级还有拥挤度，选择前多少个作为一个新的父代。剩下的都淘汰了，这个多少个就跟一开始设定的种群数一样。可想而知，一直迭代一直迭代，会越来越优秀，因为我们采用的二元锦标是选择的优秀的个体来产生子代的。最后的结果是一组解向量，所以很多编程的最后都是画图，两个目标函数的话，横纵坐标就取目标函数值。这样最后的一群解里面，有的偏向目标函数1有的偏向目标函数2。

我用python写了个代码，但是csdn懂得都懂，如果需要可以留言，我后续可能上传github。