- 1.来自github-lululxvi的代码,侵删
The code from Github ullxvi, if it infringes on your rights, please contact me to delete it. Thank you very much.
用中文注释并且修改一些地方让它能在我的电脑上运行
###具有Dirichlet/Neumann边界条件的一维泊松方程###
###问题设置###
###我们将求解泊松方程\Delta u=2,\qquad x\in[-1,1],###
###右边界上有Neumman边界条件 \left.\dfrac{du}{dx}\right | _{x=1}=4###
###和左边界上的Dirichlet边界条件 u(-1)=0 u(x)=(x+1)^2###
###实施###
###本描述逐步地完成上述泊松方程的求解器的实现。###
###首先.._Possion方程在具有狄利克雷边界条件的1D中:###https://github.com/lululxvi/deepxde/blob/master/docs/demos/poisson.1d.dirichlet.rst.###
###导入DeepXDE和TensorFlow(``tf``)模块:###
import deepxde as dde
from deepxde.backend import tf
# 我们首先定义一个计算几何。我们可以使用内置类“Interval”,如下所示#
geom = dde.geometry.Interval(-1, 1)
# 接下来,我们表示泊松方程的PDE残差:#
def pde(x, y):
dy_xx = dde.grad.hessian(y, x)
return dy_xx - 2
###“pde”的第一个自变量是网络输入,即:math:`x'-坐标。第二个参数是网络输出,即解决方案:math:`u(x)`,但这里我们使用`y`作为变量的名称。接下来,我们分别考虑Neumann边界条件和Dirichlet边界条件。Neumann边界条件由一个简单的Python函数定义。对于满足以下条件的点,函数应返回“True”:math:“x = 1”,否则返回“False”(请注意,由于舍入错误,通常明智的做法是使用“dde.utils.isclose”来测试两个浮点值是否相等)。在这个函数中,“边界”的自变量“x”是网络输入,是一个:math: `d'-dim向量,其中:math`d'是维度,在这种情况下:math:`d = 1'。然后使用布尔值“on_bboundary”作为第二个参数。如果点“x”(第一个自变量)在几何的边界上,在这种情况下,当它到达区间的右端点时是Neumann边界,那么“边界上”是“真”,否则,“边界上的”是“假”。###
def boundary_r(x, on_boundary):
return on_boundary and dde.utils.isclose(x[0], 1)
###狄利克雷边界条件的定义方式类似,对于满足以下条件的点,函数应返回“True”:math:“x=-1”“False”,否则。这个函数中的参数类似于“boundary_r”,唯一的区别是在这种情况下,当到达区间的左端点时使用狄利克雷边界条件。###
def boundary_l(x, on_boundary):
return on_boundary and dde.utils.isclose(x[0], -1)
###接下来,我们定义一个函数来返回Dirichlet边界上的点:math:'x'的值:math:'u(x)'。在这种情况下,它是:math:`u(x)=0。例如,:math:`(x+1)^2'在边界上为0,因此我们也可以使用###
def func(x):
return (x + 1) ** 2
###那么,狄利克雷边界条件是###
bc_l = dde.icbc.DirichletBC(geom, func, boundary_l)
###对于Neumann边界条件,我们不是定义一个函数来返回边界上的值:math:`u(x)',而是使用lambda函数,并且定义了Neumann边界状态###
bc_r = dde.icbc.NeumannBC(geom, lambda X: 2 * (X + 1), boundary_r)
###现在,我们已经指定了几何,PDE残差,狄利克雷边界条件和诺依曼边界条件。然后我们将PDE问题定义为###
data = dde.data.PDE(geom, pde, [bc_l, bc_r], 16, 2, solution=func, num_test=100)
###数字16是在域内采样的训练残差点的数量,数字2是在边界上采样的训练点的数量。参数“solution=func”是用于计算我们的解决方案的错误的参考解决方案,如果我们没有参考解决方案则可以忽略它。我们使用100个残差点来测试PDE残差。接下来,我们选择网络。在这里,我们使用深度为4(即3个隐藏层)、宽度为50的全连接神经网络:###
layer_size = [1] + [50] * 3 + [1]
activation = "tanh"
initializer = "Glorot uniform"
net = dde.nn.FNN(layer_size, activation, initializer)
###现在,我们有了PDE问题和网络。我们建立了一个“模型”,并选择优化器和学习率:###
model = dde.Model(data, net)
model.compile("adam", lr=0.001, metrics=["l2 relative error"])
###我们还计算了:math:'L^2'相对误差作为训练过程中的一个度量。然后,我们对模型进行10000次迭代训练:###
losshistory, train_state = model.train(iterations=10000)
第一次运行的结果
Backend TkAgg is interactive backend. Turning interactive mode on.
Compiling model...
'compile' took 0.697311 s
Training model...
Step Train loss Test loss Test metric
0 [3.99e+00, 1.06e-02, 1.54e+01] [4.00e+00, 1.06e-02, 1.54e+01] [9.78e-01]
1000 [6.12e-04, 4.04e-09, 6.06e-07] [4.37e-04, 4.00e-09, 6.06e-07] [4.53e-04]
2000 [1.47e-04, 1.01e-07, 9.52e-08] [1.43e-04, 1.01e-07, 9.55e-08] [8.40e-04]
3000 [1.68e-04, 1.76e-03, 7.50e-04] [1.71e-04, 1.76e-03, 7.50e-04] [1.36e-02]
4000 [6.82e-05, 1.56e-13, 1.28e-09] [7.26e-05, 2.22e-16, 1.31e-09] [7.42e-04]
5000 [5.40e-05, 5.65e-08, 2.18e-08] [5.79e-05, 5.64e-08, 2.18e-08] [6.67e-04]
6000 [4.29e-05, 3.79e-08, 2.54e-08] [4.65e-05, 3.80e-08, 2.57e-08] [6.58e-04]
7000 [3.87e-05, 5.36e-06, 1.08e-05] [3.89e-05, 5.36e-06, 1.08e-05] [8.30e-04]
8000 [3.39e-05, 1.51e-05, 2.40e-05] [3.31e-05, 1.51e-05, 2.40e-05] [1.27e-03]
9000 [2.33e-05, 2.44e-10, 2.27e-13] [2.53e-05, 2.37e-10, 9.09e-13] [5.08e-04]
10000 [1.78e-05, 1.14e-12, 1.00e-10] [1.91e-05, 5.66e-13, 9.09e-11] [4.62e-04]
Best model at step 10000:
train loss: 1.78e-05
test loss: 1.91e-05
test metric: [4.62e-04]
'train' took 31.522014 s
第二次运行的结果
Compiling model...
'compile' took 0.000672 s
Training model...
Step Train loss Test loss Test metric
0 [3.98e+00, 1.23e-01, 1.37e+01] [4.01e+00, 1.23e-01, 1.37e+01] [9.28e-01]
1000 [3.69e-04, 1.83e-09, 7.62e-08] [2.97e-04, 1.84e-09, 7.65e-08] [8.32e-04]
2000 [2.24e-04, 2.18e-07, 9.34e-08] [1.99e-04, 2.18e-07, 9.34e-08] [1.14e-03]
3000 [1.44e-04, 5.48e-10, 2.75e-11] [1.26e-04, 5.65e-10, 2.75e-11] [8.94e-04]
4000 [7.84e-05, 1.06e-06, 5.28e-07] [6.54e-05, 1.06e-06, 5.29e-07] [8.61e-04]
5000 [2.48e-05, 3.81e-11, 3.28e-10] [1.91e-05, 4.34e-11, 3.28e-10] [3.78e-04]
6000 [1.20e-05, 1.16e-07, 4.65e-08] [9.62e-06, 1.16e-07, 4.66e-08] [1.87e-04]
7000 [1.10e-05, 3.11e-06, 1.68e-06] [1.04e-05, 3.11e-06, 1.68e-06] [7.65e-04]
8000 [1.18e-05, 8.81e-10, 4.71e-10] [1.13e-05, 8.63e-10, 4.50e-10] [2.99e-04]
9000 [4.48e-05, 2.09e-04, 1.87e-04] [3.99e-05, 2.09e-04, 1.87e-04] [5.27e-03]
10000 [1.32e-05, 2.14e-08, 1.55e-08] [1.30e-05, 2.14e-08, 1.56e-08] [3.70e-04]
Best model at step 8000:
train loss: 1.18e-05
test loss: 1.13e-05
test metric: [2.99e-04]
'train' took 33.530548 s
第三次运行的结果
Compiling model...
'compile' took 0.000719 s
Training model...
Step Train loss Test loss Test metric
0 [3.99e+00, 2.82e-02, 1.48e+01] [4.00e+00, 2.82e-02, 1.48e+01] [9.65e-01]
1000 [9.23e-04, 1.28e-08, 2.69e-07] [7.35e-04, 1.28e-08, 2.69e-07] [1.22e-03]
2000 [1.29e-04, 4.57e-09, 8.46e-10] [1.01e-04, 4.56e-09, 8.46e-10] [8.91e-04]
3000 [3.67e-05, 1.26e-09, 1.92e-09] [3.46e-05, 1.27e-09, 1.92e-09] [4.90e-04]
4000 [3.38e-05, 8.01e-05, 3.49e-05] [3.12e-05, 8.01e-05, 3.49e-05] [2.76e-03]
5000 [2.65e-05, 4.23e-07, 2.08e-07] [2.64e-05, 4.24e-07, 2.08e-07] [6.02e-04]
6000 [3.12e-05, 1.86e-05, 4.45e-06] [2.35e-05, 1.86e-05, 4.46e-06] [2.10e-03]
7000 [2.01e-05, 1.35e-10, 2.95e-10] [2.02e-05, 1.30e-10, 2.95e-10] [4.36e-04]
8000 [1.77e-05, 2.45e-10, 1.54e-10] [1.79e-05, 2.44e-10, 1.78e-10] [4.16e-04]
9000 [3.14e-05, 1.01e-06, 2.67e-05] [2.68e-05, 1.01e-06, 2.67e-05] [6.01e-04]
10000 [1.42e-05, 4.22e-11, 1.54e-10] [1.45e-05, 3.99e-11, 1.54e-10] [3.88e-04]
Best model at step 10000:
train loss: 1.42e-05
test loss: 1.45e-05
test metric: [3.88e-04]
'train' took 32.801695 s不知道为什么,运行不同的次数结果不同。
- 2.来自github-HaoZhongkai的二维的可视图片的代码
import deepxde as dde
def pde(x, y):
dy_xx = dde.grad.hessian(y, x, i=0, j=0)
dy_yy = dde.grad.hessian(y, x, i=1, j=1)
return -dy_xx - dy_yy - 1
def boundary(_, on_boundary):
return on_boundary
geom = dde.geometry.Polygon([[0, 0], [1, 0], [1, -1], [-1, -1], [-1, 1], [0, 1]])
bc = dde.DirichletBC(geom, lambda x: 0, boundary)
data = dde.data.PDE(geom, pde, bc, num_domain=1200, num_boundary=120, num_test=1500)
net = dde.maps.FNN([2] + [50] * 4 + [1], "tanh", "Glorot uniform")
model = dde.Model(data, net)
model.compile("adam", lr=0.001)
model.train(epochs=50000)
model.compile("L-BFGS")
losshistory, train_state = model.train()
dde.saveplot(losshistory, train_state, issave=True, isplot=True)以下是运行结果
Compiling model...
'compile' took 0.000721 s
Warning: epochs is deprecated and will be removed in a future version. Use iterations instead.
Training model...
Step Train loss Test loss Test metric
0 [1.02e+00, 1.66e-04] [1.02e+00, 1.66e-04] []
1000 [2.20e-04, 3.24e-03] [2.15e-04, 3.24e-03] []
2000 [1.63e-04, 2.39e-03] [1.34e-04, 2.39e-03] []
3000 [2.28e-04, 1.68e-03] [1.76e-04, 1.68e-03] []
4000 [2.58e-04, 8.96e-04] [1.90e-04, 8.96e-04] []
5000 [1.18e-04, 4.34e-04] [7.87e-05, 4.34e-04] []
6000 [9.05e-05, 2.69e-04] [6.94e-05, 2.69e-04] []
7000 [6.91e-05, 2.07e-04] [5.07e-05, 2.07e-04] []
8000 [1.12e-04, 1.93e-04] [9.80e-05, 1.93e-04] []
9000 [1.37e-04, 1.85e-04] [1.15e-04, 1.85e-04] []
10000 [4.91e-05, 1.62e-04] [3.83e-05, 1.62e-04] []
11000 [4.16e-05, 1.50e-04] [3.37e-05, 1.50e-04] []
12000 [7.26e-05, 1.44e-04] [6.97e-05, 1.44e-04] []
13000 [4.07e-05, 1.39e-04] [3.53e-05, 1.39e-04] []
14000 [8.53e-05, 1.39e-04] [8.31e-05, 1.39e-04] []
15000 [1.11e-03, 2.26e-04] [1.09e-03, 2.26e-04] []
16000 [3.55e-05, 1.26e-04] [2.84e-05, 1.26e-04] []
17000 [4.31e-05, 1.20e-04] [3.95e-05, 1.20e-04] []
18000 [2.12e-05, 1.16e-04] [1.63e-05, 1.16e-04] []
19000 [1.06e-03, 1.14e-04] [1.04e-03, 1.14e-04] []
20000 [4.72e-04, 1.11e-04] [4.41e-04, 1.11e-04] []
21000 [1.82e-05, 1.09e-04] [1.45e-05, 1.09e-04] []
22000 [4.75e-05, 1.18e-04] [4.42e-05, 1.18e-04] []
23000 [1.58e-05, 1.05e-04] [1.27e-05, 1.05e-04] []
24000 [1.74e-05, 1.04e-04] [1.55e-05, 1.04e-04] []
25000 [1.59e-05, 1.01e-04] [1.38e-05, 1.01e-04] []
26000 [1.42e-05, 9.98e-05] [1.17e-05, 9.98e-05] []
27000 [5.25e-04, 9.82e-05] [5.23e-04, 9.82e-05] []
28000 [2.19e-05, 9.62e-05] [2.12e-05, 9.62e-05] []
29000 [8.01e-05, 9.90e-05] [7.57e-05, 9.90e-05] []
30000 [1.55e-05, 9.41e-05] [1.34e-05, 9.41e-05] []
31000 [1.28e-05, 9.03e-05] [1.12e-05, 9.03e-05] []
32000 [1.77e-05, 8.87e-05] [1.65e-05, 8.87e-05] []
33000 [1.29e-05, 8.76e-05] [1.16e-05, 8.76e-05] []
34000 [1.17e-05, 8.55e-05] [1.08e-05, 8.55e-05] []
35000 [2.63e-04, 8.44e-05] [2.40e-04, 8.44e-05] []
36000 [1.29e-05, 8.26e-05] [1.23e-05, 8.26e-05] []
37000 [1.10e-05, 7.96e-05] [1.13e-05, 7.96e-05] []
38000 [2.10e-05, 8.11e-05] [2.00e-05, 8.11e-05] []
39000 [9.77e-06, 7.62e-05] [9.58e-06, 7.62e-05] []
40000 [1.71e-05, 7.42e-05] [1.68e-05, 7.42e-05] []
41000 [1.10e-05, 7.22e-05] [1.15e-05, 7.22e-05] []
42000 [9.98e-06, 7.14e-05] [9.77e-06, 7.14e-05] []
43000 [9.09e-06, 6.93e-05] [9.46e-06, 6.93e-05] []
44000 [1.66e-04, 7.71e-05] [1.74e-04, 7.71e-05] []
45000 [1.07e-05, 6.78e-05] [1.03e-05, 6.78e-05] []
46000 [8.64e-06, 6.50e-05] [9.01e-06, 6.50e-05] []
47000 [1.45e-05, 6.68e-05] [1.41e-05, 6.68e-05] []
48000 [2.07e-05, 6.27e-05] [1.87e-05, 6.27e-05] []
49000 [1.06e-04, 6.29e-05] [9.81e-05, 6.29e-05] []
50000 [2.19e-05, 5.91e-05] [1.97e-05, 5.91e-05] []
Best model at step 46000:
train loss: 7.36e-05
test loss: 7.40e-05
test metric: []
'train' took 764.109310 s
Compiling model...
'compile' took 0.000607 s
Training model...
Step Train loss Test loss Test metric
50000 [2.19e-05, 5.91e-05] [1.97e-05, 5.91e-05] []
51000 [9.07e-06, 1.91e-05] [1.53e-05, 1.91e-05] []
52000 [5.17e-06, 1.06e-05] [1.09e-05, 1.06e-05] []
53000 [3.65e-06, 5.35e-06] [1.71e-05, 5.35e-06] []
54000 [1.92e-06, 3.39e-06] [2.48e-05, 3.39e-06] []
55000 [1.36e-06, 2.90e-06] [2.76e-05, 2.90e-06] []
56000 [1.35e-06, 2.89e-06] [2.76e-05, 2.89e-06] []
57000 [1.35e-06, 2.89e-06] [2.77e-05, 2.89e-06] []
58000 [1.35e-06, 2.88e-06] [2.78e-05, 2.88e-06] []
59000 [1.35e-06, 2.88e-06] [2.78e-05, 2.88e-06] []
60000 [1.35e-06, 2.88e-06] [2.78e-05, 2.88e-06] []
61000 [1.35e-06, 2.87e-06] [2.79e-05, 2.87e-06] []
62000 [1.35e-06, 2.87e-06] [2.79e-05, 2.87e-06] []
63000 [1.35e-06, 2.87e-06] [2.80e-05, 2.87e-06] []
64000 [1.35e-06, 2.87e-06] [2.80e-05, 2.87e-06] []
65000 [1.35e-06, 2.86e-06] [2.80e-05, 2.86e-06] []
Best model at step 65000:
train loss: 4.21e-06
test loss: 3.09e-05
test metric: []
'train' took 277.292921 s
Saving loss history to D:\PycharmProjects\pythonProject\pythonProject1\loss.dat ...
Saving training data to D:\PycharmProjects\pythonProject\pythonProject1\train.dat ...
Saving test data to D:\PycharmProjects\pythonProject\pythonProject1\test.dat ...
以下是运行图片

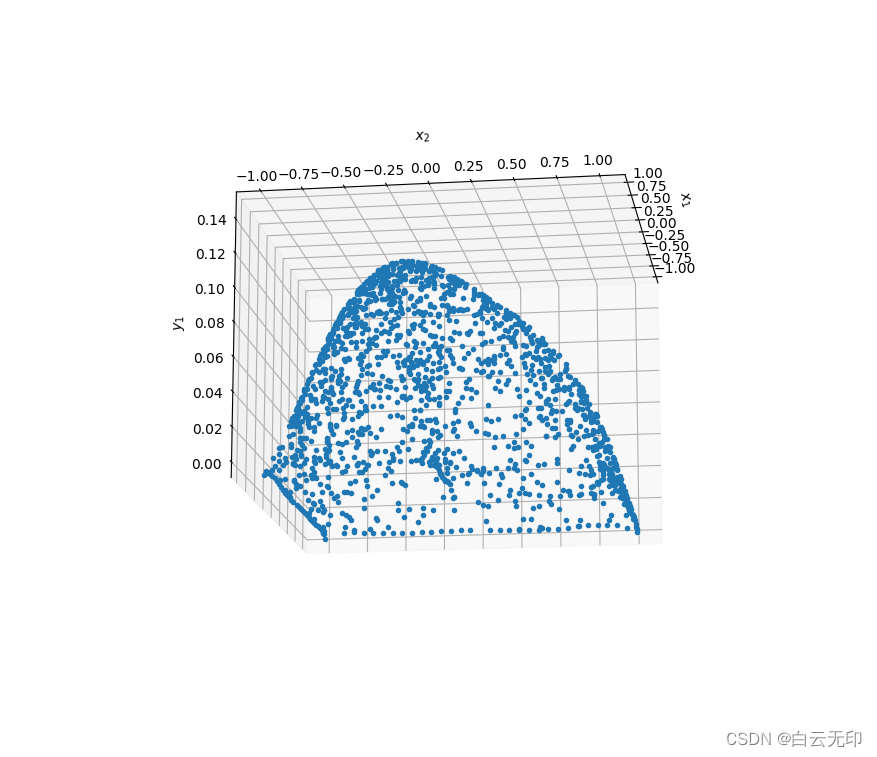
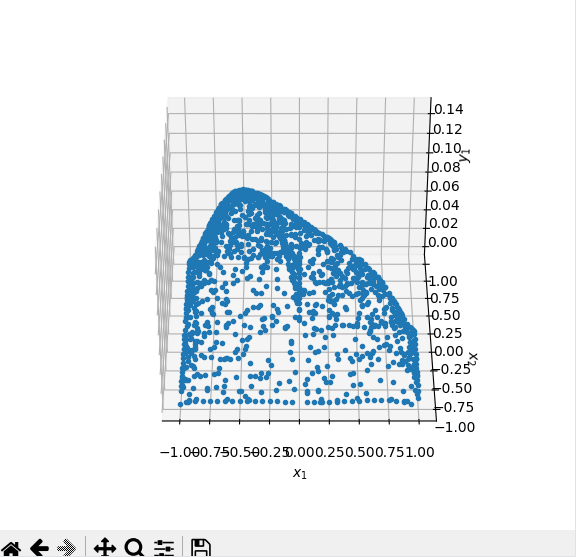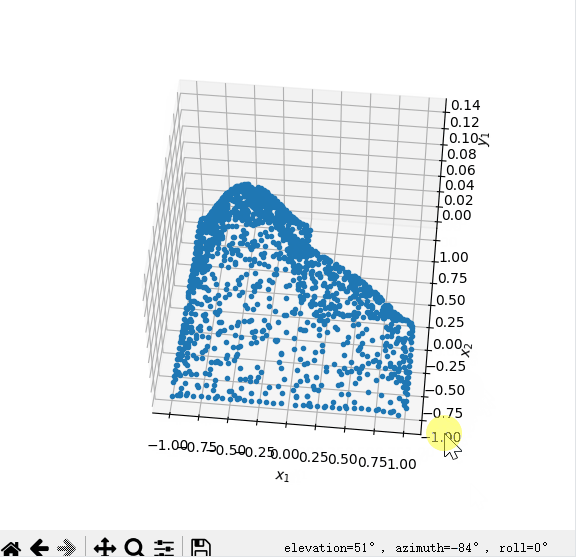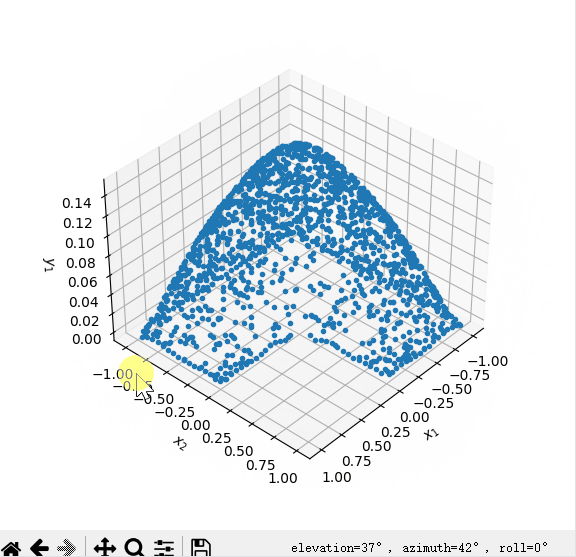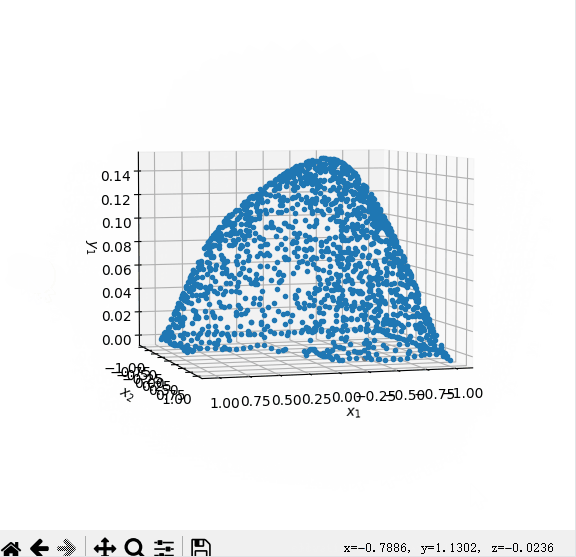
生成了dat文件,下一步去研究
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








