【专题】环形染色问题

本文转载自 知乎，本文在原文的基础上做出了如下改进：

• 重绘了所有插图；
• 将知乎所有公式图片换成 $\text{LATEX}$。

---

如图所示，一个圆环被分成 $m(m\ge 2)$ 块，用 $n(n\ge 2)$ 种不同颜色给每一块染色，要求相邻两块的颜色不相同。此类问题称之为环形染色问题。

环形染色问题可以分为两种，一类是圆环中心区域要染色，一类是圆环中心区域不染色。因为中心区域染色问题在给中心涂色之后，剩余部分即为中心区域不染色的问题，所以本文重点讲解中心区域不染色问题。

本文先针对 $m=4$、$m=5$ 以分类与分步的做法解决，而后给出此类问题的通解。

中心区域不染色

$m=4,n=4$ 的情况

如图，环形区域被分成 $4$ 块，用 $4$ 种不同的颜色给这 $4$ 块区域染色，要求相邻区域颜色不同。

解：

我们先给四块区域标注为 $A,B,C,D$。先给 $A$ 染色，则有 $4$ 种颜色，而后 $B$ 有三种，$C$ 也是有三种，但是 $D$ 则需要分类来讨论。因为 $D$ 与 $A,C$ 都相邻，且 $A,C$ 都已经涂好颜色，则 $A,C$ 若同色，则 $D$ 有三种颜色可选，$A,C$ 不同色，则 $D$ 只有两种颜色可以选择，如下图所示：

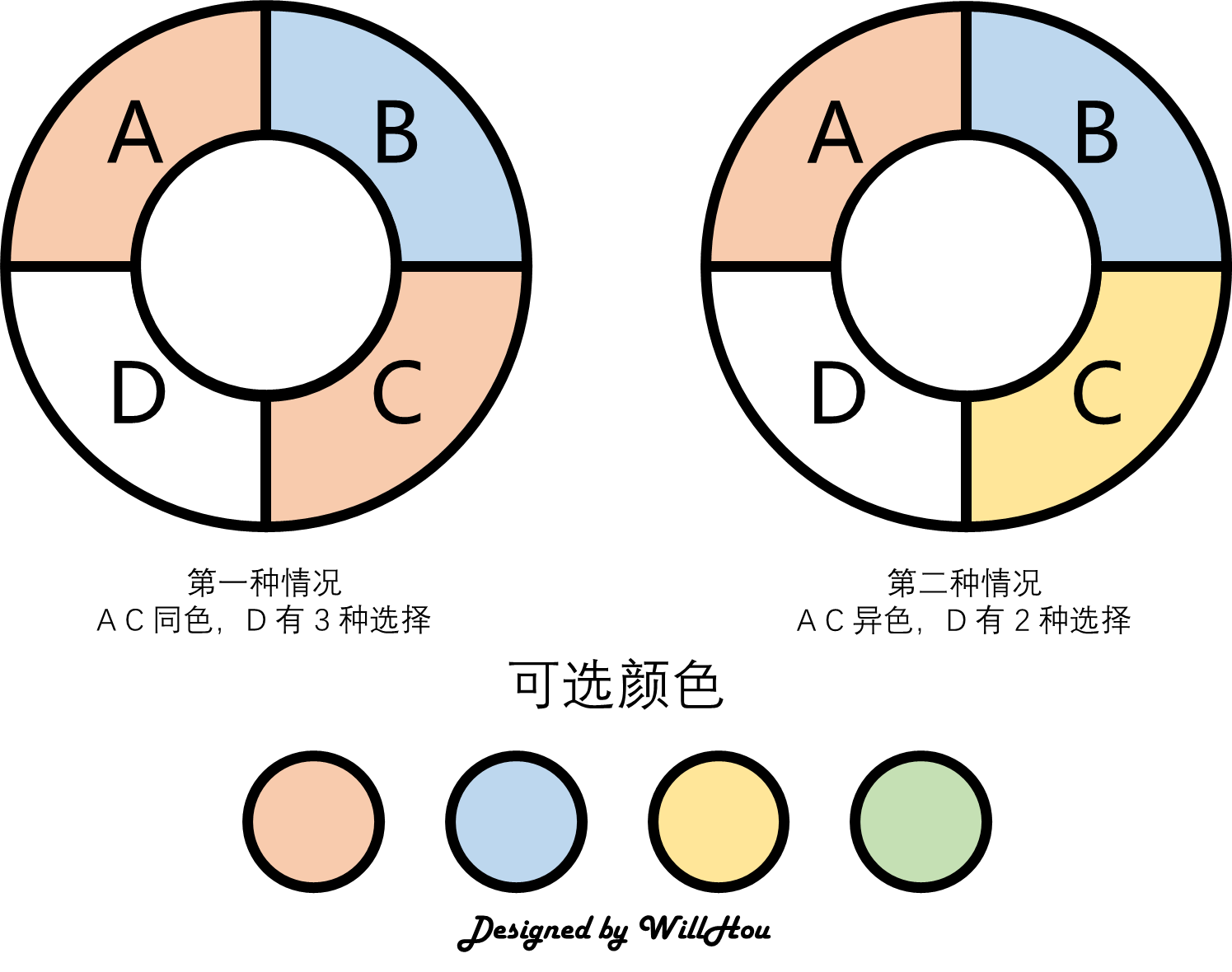
则共有 $4\times 3\times (1\times 3+2\times 2)=84$ 种染色方式。

$m=5,n=4$ 的情况

如图，环形区域被分成 $5$ 块，用 $4$ 种不同的颜色给这 $5$ 块区域染色，要求相邻区域颜色不同。

解：

同上，给五块区域标注为 $A,B,C,D,E$。依旧是按顺序给 $5$ 块区域染色。则在考虑 $A,D$ 同色问题时，需考虑到 $A,C$ 是否同色。若 $A,C$ 同色，则 $A,D$ 必定不同色。只有 $A,C$ 不同色，才有可能出现 $A,D$ 同色。

因此有以下分类：

1. $A,C$ 同色：则 $A,D$ 必定不同色，则五块区域一次有 $4,3,1,3,2$ 种选法，共有 $4\times 3\times 1\times 3\times 2=72$ 种染色方式；
2. $A,C$ 不同色：
   1. $A,D$ 同色：则五块区域依次有 $4,3,2,1,3$ 种选法，共有 $4\times 3\times 1\times 3\times 2=72$ 种染色方式；
   2. $A,D$ 异色：则五块区域依次有 $4,3,2,2,2$ 种选法，共有 $4\times 3\times 2\times 2\times 2=96$ 种染色方式；

共计有 $72+72+96=240$ 种染色方式。

任意 $m\ge 2,n\ge 2$ 的情况

记当有 $m$ 块区域时，染色方法有 $a_m$ 种；则当 $m$ 取 $1,2,3,\dots$ 时，分别有 $a_1,a_2,a_3,\dots$ 种染色方式。

首先考虑直线型染色：如下图所示，有 $m$ 块区域，$n$ 种颜色，要求相邻区域不同色。

则除了第一块有 $n$ 种涂法，其余各块都是 $n-1$ 种。则共有 $n(n-1{)}^{m-1}$ 种染色方式。

现在把直线型的两端对接，拼成一个环形。

当两端颜色相同时，首尾对接则会出现有两块相邻区域颜色相同。其余相邻区域颜色则均不同。此时若把相邻颜色相同的区域合并为一个区域，则此时的环形有 $m-1$ 块区域，任意相邻区域颜色均不相同，对应 $a_{m-1}$ 种染色方式。

当两端颜色不同时，首尾对接，则任意相邻区域颜色均不相同，此时的环形有 $m$ 块区域，对应 $a_m$ 种染色方式。

因此有 $a_m+a_{m-1}=n(n-1{)}^{m-1}$

对其稍作变形，有：
$$\begin{array}{rl}{a}_m+a_{m-1}& =(n-1)(n-1{)}^{m-1}+(n-1{)}^{m-1}\\ & =(n-1{)}^m+(n-1{)}^{m-1}\end{array}$$
移向可得：
$$a_m-(n-1{)}^m=-(a_{m-1}-(n-1{)}^{m-1})$$
分类讨论如下：

1. $a_m-(n-1{)}^m=0$

   即 $a_m=(n-1{)}^m$，考虑 $a_2=n(n-1)$，与之矛盾，舍；

2. $a_m-(n-1{)}^m\ne 0$

   令 $b_m=a_m-(n-1{)}^m$，则有 $\frac{b_m}{b_{m-1}}=-1$，为等比数列

   则 $b_m=(-1{)}^{m-2}\times b_2=(-1{)}^m\times b_2$

   代入 $b_2=a_2-(n-1{)}^2=n(n-1)-(n-1{)}^2=n-1$

   有 $b_m=(-1{)}^m\times b_2=(-1{)}^m\times (n-1)$

   代入 $b_m=a_m-(n-1{)}^m$

   有 $a_m=(n-1{)}^m+(-1{)}^m\times (n-1)$

验证一下：

1. 代入 $m=4,n=4$，有 $3^4+3=84$
2. 代入 $m=5,n=4$，有 $3^5-3=240$

中心区域染色

圆环有 $m$ 块区域，再加上中心区域共有 $m+1$ 块区域，有 $n+1$ 种颜色

由于中心区域与外环所有区域均相邻，则先涂中心区域，有 $n+1$ 种涂色方法；

此时余下 $m$ 块区域与 $n$ 种颜色，即为中心不染色时 $m$ 块区域和 $n$ 种颜色的环形染色问题，代入上述公式，共有 $a_m=(n-1{)}^m+(-1{)}^m\times (n-1)$ 种染色方法。

合计共有 $(n+1)\times a_m=(n+1)\times [(n-1{)}^m+(-1{)}^m\times (n-1)]$ 种染色方法。