算法学习（二）—— 十种排序算法的总结和分析

算法的海洋浩瀚无边！只有不断的学习，才能不断的进步，下面是自己学习过程当中对排序相关算法的笔记和总结，参考资料均来自网络。

一、排序算法概论

排序算法，就是如何使得记录按照要求排列的方法。本文一共总结了十总排序算法，如下图所示。

二、交换排序

2.1 冒泡排序

【算法说明】：最简单的、稳定的排序算法。

【算法思想】：不断比较相邻的两个数，让较大的元素不断地往后移。经过一轮比较，就选出最大的数；经过第2轮比较，就选出次大的数，以此类推。

【算法模拟】：下面以对 [ 3  2  4  1 ] 进行冒泡排序说明。

第一轮 排序过程：

[ 3  2  4  1 ]   （最初）

[ 2  3  4  2 ]   （比较3和2，交换）

[ 2  3  4  1 ]   （比较3和4，不交换）

[ 2  3  1  4 ]   （比较4和1，交换）

第一轮结束，最大的数4已经在最后面，因此第二轮排序只需要对前面三个数进行再比较。

第二轮 排序过程：

[ 2  3  1  4 ]（第一轮排序结果）

[ 2  3  1  4 ]（比较2和3，不交换）

[ 2  1  3  4 ]（比较3和1，交换）

第二轮结束，第二大的数已经排在倒数第二个位置，所以第三轮只需要比较前两个元素。

第三轮 排序过程：

[ 2  1  3  4 ] （第二轮排序结果）

[ 1  2  3  4 ] （比较2和1，交换）

至此，排序结束。

【算法实现】：

#include
      
      
       
       
#include
       
       
        
        

#define N 8

void bubble_sort(int a[],int n);


//一般实现
void bubble_sort(int a[],int n)//n为数组a的元素个数
{
    //一定进行n-1轮比较
    for(int i=0; i
        
        
         
          a[j+1])
            {
                int temp = a[j];
                a[j] = a[j+1];
                a[j+1]=temp;
            }
        }
    }
}

//优化实现
void bubble_sort_better(int a[],int n)//n为数组a的元素个数
{
    //最多进行N-1轮比较
    for(int i=0; i
         
         
          
           a[j+1])
            {
                isSorted = false;
                int temp = a[j];
                a[j] = a[j+1];
                a[j+1]=temp;
            }
        }
        if(isSorted) break; //如果没有发生交换，说明数组已经排序好了
    }
}


int  main()
{
    int num[N] = {89, 38, 11, 78, 96, 44, 19, 25};

    bubble_sort(num, N); //或者使用bubble_sort_better(num, N);

    for(int i=0; i
          
          
         
         
        
        
       
       
      
      

2.2 快速排序

【算法说明】：快排是冒泡排序的改进版，也是实际项目中最长用到的排序算法。理解快排主要分两点：分治 + 递归 ，分治是指根据一个基数将序列分成两块，左子块<右子块；递归是指按分治思想一直分下去，直到子块只有一个元素的时候停止，此时已经排好序了。

【算法思想】：将所要进行排序的数分为左右两个部分，其中一部分的所有数据都比另外一部分的数据小，然后将所分得的两部分数据进行同样的划分，重复执行以上的划分操作，直到所有要进行排序的数据变为有序为止。

【算法模拟】 ：下面以对 [32  12  7  78  23  45 ] 进行快速排序进行说明。

 

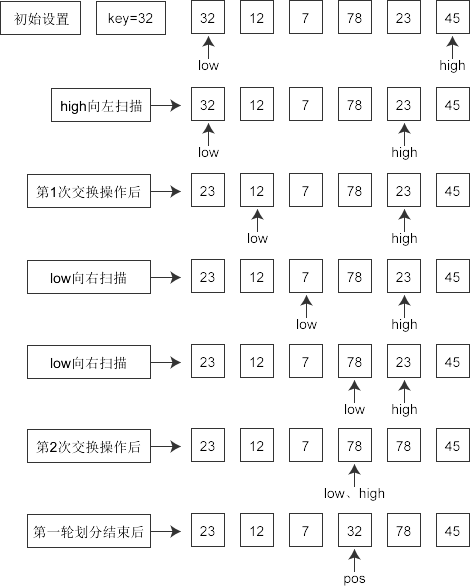【算法实现】：

#include 
       
       
        
        
#include 
        
        
         
         
#define N 6

int partition(int arr[], int low, int high){
    int key;
    //取第一个元素为key
    key = arr[low];
    while(low
         
         
          
          =key时移动high索引
        while(low 
          
          
           
           = key )
            high--;
        if(low
           
           
             key元素，把该元素移到high索引位置 && hign前移一位 arr[high--] = arr[low]; } //当low=high时，空位放key结束排序。 arr[low] = key; return low; } void quick_sort(int arr[], int start, int end){ int pos; if (start 
             
           
          
          
         
         
        
        
       
       

三、选择排序

3.1 直接选择排序

【算法说明】：选择排序是一种不稳定的排序算法，可能会打乱两个相同数字的原有顺序。

【算法思想】：选择排序（从小到大）的基本思想是，首先，选出最小的数，放在第一个位置；然后，选出第二小的数，放在第二个位置；以此类推，直到所有的数从小到大排序。

【算法模拟】：在实现上，我们通常是先确定第i小的数所在的位置，然后，将其与第i个数进行交换。下面以对 [  3  2  4  1 ] 进行选择排序说明，使用min_index 记录当前最小的数所在的位置。

   第1轮 排序过程 （寻找第1小的数所在的位置）

   [ 3  2  4  1 ]（最初， min_index=1）

   [ 3  2  4  1 ]（3 > 2， 所以min_index=2）

   [ 3  2  4  1 ]（2 < 4， 所以 min_index=2）

   [ 3  2  4  1 ]（2 > 1， 所以 min_index=4， 这时候确定了第1小的数在位置4）

   [ 1  2  4  3 ]（第1轮结果，将3和1交换，也就是位置1和位置4交换） 

    第2轮 排序过程 （寻找第2小的数所在的位置）

   [ 1  2  4  3 ]（第1轮结果， min_index=2，只需要从位置2开始寻找）

   [ 1  2  4  3 ]（4 > 2， 所以min_index=2）

   [ 1  2  4  3 ]（3 > 2， 所以 min_index=2）

   [ 1  2  4  3 ]（第2轮结果，因为min_index位置刚好在第2个位置，无需交换） 

     

    第3轮 排序过程 （寻找第3小的数所在的位置）

   [ 1  2  4  3 ]（第2轮结果， min_index=3，只需要从位置2开始寻找）

   [ 1  2  4  3 ]（4 > 3， 所以min_index=4）

   [ 1  2  3  4 ]（第3轮结果，将3和4交换，也就是位置4和位置3交换） 

    至此，排序完毕。

【算法实现】：

#include
        
        
         
         
#include
         
         
          
          

#define N 8

void select_sort(int a[],int n);


//选择排序实现
void select_sort(int a[],int n)//n为数组a的元素个数
{
    //进行N-1轮选择
    for(int i=0; i
          
          
         
         
        
        




3.2 堆排序

要想理解堆排序，先要知道什么是堆，怎么建立堆，怎么操作堆中的元素，要说清楚堆排序，篇幅太长，

所以找了一个讲的很详细的博客，可以点击进去学习堆排序的相关知识：

http://www.cnblogs.com/mengdd/archive/2012/11/30/2796845.html

四、插入排序

4.1 直接插入排序

【算法说明】：插入排序是排序算法的一种，它不改变原有的序列（数组），而是创建一个新的序列，在新序列上进行操作。

【算法思想】：插入排序的基本思想是，将元素逐个添加到已经排序好的数组中去， 同时要求，插入的元素必须在正确的位置，这样原来排序好的数组是仍然有序的。

【算法模拟】： 下面，以对[ 3  2  4  1 ] 进行选择排序说明插入过程，使用j记录元素需要插入的位置。排序目标是使数组从小到大排列。  

第1轮

[ 3 ]  [ 2  4  1 ]  （最初状态，将第1个元素分为排序好的子数组，其余为待插入元素）

[ 3 ]  [ 2  4  1 ]  （由于3>2，所以待插入位置j=1）

[ 2  3 ]  [ 4  1 ]  （将2插入到位置j）  

第2轮

[ 2  3 ]  [ 4  1 ]  （第1轮排序结果）

[ 2  3 ]  [ 4  1 ] （由于2<4，所以先假定j=2） 

[ 2  3 ]  [ 4  1 ] （由于3<4，所以j=3） 

[ 2  3  4 ]  [ 1 ] （由于4刚好在位置3，无需插入）  

第3轮 

[ 2  3  4 ]  [ 1 ] （第2轮排序结果） 

[ 2  3  4 ]  [ 1 ] （由于1<2，所以j=1）

【算法实现】：

/*
稳定性：稳定的
思想：先将原序列分为有序区和无序区，然后再经过
      比较和后移操作将无序区元素插入到有序区中
*/
//插入排序实现,这里按从小到大排序
//插入排序算法(升序排列)
void insertionSort(int *array, int len)
{
    int j = 0;
    int tmp = 0;    // 存储基准数
    // 遍历无序序列
    for (int i = 1; i < len; ++i)
    {
        if (array[i] < array[i-1])
        {
            tmp = array[i];
            // 遍历有序序列(从后往前)
            for (j = i - 1; j>=0 && array[j] > tmp; --j)
            {
                // 有序序列元素后移
                array[j + 1] = array[j];
            }
            // 填坑,其实是填循环里的a[j],+1是因为做了--j操作。
            array[j+1] = tmp;
        }
    }
}

4.2 希尔（Shell）排序

【算法说明】：一

【算法思想】：一

【算法模拟】： 下

【算法实现】：一

五、归并排序

5.1 归并排序

【算法说明】：一

【算法思想】：一

【算法模拟】： 下

【算法实现】：一

六、计数排序

6.1 计数排序

【算法说明】：一

【算法思想】：一

【算法模拟】： 下

【算法实现】：一

七、桶排序

7.1 桶排序

【算法说明】：一

【算法思想】：一

【算法模拟】： 下

【算法实现】：一

八、基数排序

8.1 基数排序

【算法说明】：一

【算法思想】：一

【算法模拟】： 下

【算法实现】：一