概率机器人（1）：有关概率的基本概念

最新推荐文章于 2024-03-05 11:23:00 发布

精谷粒

最新推荐文章于 2024-03-05 11:23:00 发布

阅读量664

点赞数 3

文章标签：概率论

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/wl1234567891/article/details/117354536

版权

本文介绍了概率机器人中的基本概念，包括随机变量（离散与连续）、概率、概率密度函数（如正态分布）、联合分布、条件概率、全概率定理、贝叶斯准则、期望和熵。这些概念在传感器测量、控制和状态估计等领域中至关重要。

摘要由CSDN通过智能技术生成

目录

3.概率密度函数

6.全概率定理

7.贝叶斯准则（很重要）

1.随机变量

在概率机器人建模时，如传感器测量、控制、机器人的状态及其环境这些都作为随机变量。随机变量分为离散随机变量和连续随机变量。

2.概率

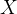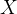令 $X$ 为一个随机变量， $x$ 表示 $X$ 的某一个特定值，那么 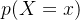$p(X=x)$ ，一般可简写成 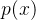$p(x)$ ，代表随机变量 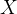$X$ 具有 $x$ 值的概率。

3.概率密度函数

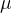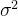连续随机变量都拥有概率密度函数，普通概率密度函数都是具有均值 $\mu$ 和方差 $\sigma ^{2}$ 的一维正态分布。

正态分布的概率密度函数为： $p(x)=(2\pi \sigma ^{2})^{-\frac{1}{2}}e^{-\frac{1}{2}\frac{(x-\mu )^{2}}{\sigma ^{2}}}$ 。

多元正态分布的密度函数为：

最低0.47元/天解锁文章

关注

3
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
复制链接

分享到 QQ

分享到新浪微博

扫一扫

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。