网上存在很多对该问题的解答,但是很多解答都有错误,比较正确的是http://blog.csdn.net/lyso1/article/details/5399146,但是问题解法较为复杂,在此将从另一个思路对问题进行解答,很大程度简化了算法正确性的证明。
------------------------------------------------------------------------------------------------------------------------------------------
问题1. 写一个程序,对于一个64位正整数,输出它所有可能的连续自然数(两个以上)之和的算式;
问题2. 例如32就找不到这样的表达,这样的数字有什么规律?
问题3. 在64位正整数中,子序列数目最多的是哪一个?能否用数学知识推导出来?
------------------------------------------------------------------------------------------------------------------------------------------
将一个正整数表示成连续自然数之和,即N=s+(s+1)+(s+2)+…+(e-1)+e。利用等差数列求和公式,我们有
也即2N=(s+e)(e-s+1),该等式表示可以将2N分解成两个正整数的乘积。我们设x=s+e, y=e-s+1(其中x>y)。利用x、y我们可以求解获得s和e:
因为s和e都是整数,因而为了使上面的式子能整除,则x和y必须一奇一偶。因为2N=xy,2N含有偶因子,所以N必须含有奇因子才能使等式成立。这也就证明了N能表示成连续自然数的充要条件:N必须含有奇数因子,问题二得证。
利用公式(2),我们即可获得正整数N的一个连续自然数序列。为了输出所有的连续自然数序列,我们需要获得所有的x和y组合,也即求2N的所有因子组合。我们可以利用算法基本定理将2N分解成有限个质数的乘积:
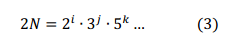
我们将2N按照质因子进行分解,由于x和y只有一个偶数,所以2N的分解式中质因子2的所有组合都只能在其中一个数中,否则x和y都是偶数。不妨假设x是偶数,则
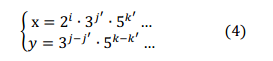
其中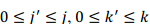
问题三按照网上的资料,有两种理解方式:1)、可以表示为最多个序列的那个数;2)、序列中项最多的那个数。但是按照题意其实应该是第一种理解方式。由于质因子2只能在x和y的某一个数中,对质因子分解不起作用,所以为了让序列个数尽可能多,N的质因子中不能包含2。因此若让子序列个数最多,则即(j+1) (k+1)…最大。通过简单分析我们可以获得具有最多序列个数的正整数j、k等质因子指数的两个性质:

性质一可以通过替换来证明,假设当前的最大序列个数不满足性质一,设第一个不满足性质的两个指数为a和b,满足a<b。由于序列个数为(j+1) ∙ (k+1) ∙…,我们通过将两个质因子的指数交换可以获得相同的序列个数。此外,由于前面的质因子小,交换之后总的乘积会变小,从而可能产生一个更大的指数,使序列个数更多。通过这样依次交换不满足性质的相邻两个指数,最终我们会得到满足性质一并且使序列个数最多的指数序列。这也与经验相吻合,要想使序列个数尽可能多,则正整数必须尽量少含有大的质因子。对于性质二,当正整数只包含质因子3时,质因子之和最大,此时为40。而当正整数含有越多较大的质因子时,则质因子之和就越小,在满足性质一的前提下,当正整数等于3 ∙5 ∙…∙53时,和最小,此时共有15个质因子,含有的序列个数为2^15-1。该正整数含有的序列个数已经非常多,但不一定是最多,例如将53替换为27,则序列个数升为5∙2^13-1。如果我们继续替换,将3^4 ∙5 ∙…∙47变为3^3 ∙5^2 ∙…∙47,则序列个数又升为6∙2^13-1。该数可能已经是具有最多序列的数,但是要想获得准确的最大序列个数,我们还需要利用性质一二去遍历所有可能的情况。如果按照第二种理解方式,则我们可以证明具有最多项的数N的最多项必从1开始。假设最多项不从1开始而是从s(s>1)开始,则我们可以将该最多项的每一项均减去s-1,则最多项等价于从1开始的最多项,也即我们至少可以构造和之前的最多项一样长的新序列。此外,由于每一项均减少了s-1,如果此时减少的和大于最多项的最大项,我们还可以添加新的项到最多项的末尾,产生更长的最多项。
对问题一:
最高效的解决方法是:找出2*n的所有质因子,然后再组合这些质因子。 可以用一个队列保存前m个因子的组合结果。(该队列所用的内存并不大。)
另见: 输出和为n的所有的连续自然数序列 输出自然数n的所有因子
对问题二:
要使n不能拆分,则说明两组拆分 (2^t * a, b) 和 (a, 2^t * b)都不能存在。 因而 min(2^t * a, b) < 2, min(2^t * b, a) < 2 (即都不满足k值>=2)
因而 b < 2 且 a < 2 即 a = b = 1, n = 2^(t-1) 因而: 当n等于2的t次幂时,n不能被拆分。
对问题三:
显然,拆分个数,只与奇质因子的数目有关。
2 ^ 64 = 1.8e19
3 * 5 *7 *11 *13 *17 * 19 *23 *29 *31 * 37 *41 * 43 *47 *53 = 1.6e19
假设N是有最多因子个数的最小64位奇数,设 N = 3^a3 * 5^a5 * 7^a7 … 则一定有 a3 >= a5 >= a7 … 否则只要交换不满足条件的那两个数,得到相同因子个数但比N更小的数,这与假设矛盾。
S = 2 ^ 64 = 1.8e19
M=3*5*7*11*13*17*19*23*29*31*37*41*43*47*53=1.6e19(因子个数2^15)
因而,N的最大质因子一定小等于53
由S / (M / 53) = 60 可将60拆分成3^3(因子数5*2^13) 3^2 * 5(因子数3*2^14)
可得局部最优解:R1 = 3^3 *5^2 *7*11*13*17*19*23*29*31*37*41*43*47
如果N不等于R1,则a47 = 0(要将S / (M / 53/47)) = 2820 拿出来拆分)
若N包含k个质因子a, t为满足a^t > 47(显然t >= 2)的最小整数,则 k < 2*t-1
(否则若将t个a拆分成47,由 (k+1)*1 – (k-t+1) * 2 = 2*t-k-1 <=0,
可知拆分后得到的数更优,与N最优矛盾)。
因此a3 <=2*4-2=6,
a5 <= 2*3 – 2 = 4,
a7 <= 2*2-2 = 2
a11 <= 2*2-2 = 2
若a7 <=1, 则a3<=4,否则可以将2个3拆成1个7,得到更优解。由S/(3^4*5^4)/ (7*11*13*17*19*23*29*31*37*41) = 35(能得到的最多因子个数为25*2^10 < 3*2^14不是最优解)因而 a7 = 2
( 若az = 2, ax = a, ay =b 且 z > x * y,若不能将 z拆分成 x * y,则有 (a+1)*(b+1)*3 > (a+2)*(b+2)*2,即 (a-1)*(b-1) >= 7 )
若a23=2则可将1个23拆成3和7,由 (1+a3)*3*3 – (1+a3+1)*4*2 = a3-7<0可知得到的数更优,与假设矛盾,因而 a23<=1,
由于 S/(3^6*5^4)/(7*11*13*17*19)^2 = 387 > 23因而 一定含有因子23,a23 = 1
若a31=0,则 a5 = 2(否则,5*7合并成31,得到更优解)由 2^64 / (3^6*(5*7*11*13*17*19)^2 * 23 * 29) = 14可知,该情况下得到的最大数不是最优, 因而 a31 = 1
(若a17 =2则 a3>=5, a5=3 或 a3>=4 a5=4,否则可以将17拆分成3*5)
利用前面的结论, a3 >= a5 >= a7 …
a3 <= 6 a5 <= 4 a7 = 2 a23 = 1 a31 = 1 a47 = 0
可在较短时间内搜索出满足上述条件的因子个数最多的奇数,再与局部最优解R1进行比较,就可以确定最优解。
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------= (i + i+k-1)*k/2
=(2*i+k-1)*k/2
=k*(i+ (k-1)/2)
=k*i + k*(k-1)/2
判断条件: num%(k*(k-1)/2)==0 或者 2*num>k*(k-1) 得: k<sqrt(2*num) 。 i=num/k;可得出i。
- #include<iostream>
- using namespace std;
- void AddNum(__int64 num)
- {
- __int64 k;
- __int64 i,t;
- __int64 j;
- int flag=-1;
- for (k=2;num>j;k++)//判断条件也可用sqrt(2*num),但是sqrt对64位的不好用。
- {
- if (k%2==0)
- {
- j=(k/2)*(k-1);//这样判断是为了节省计算的时间,因为k*(k-1)/2比(k/2)*(k-1)更费时间
- }
- else
- {
- j=((k-1)/2)*k;
- }
- if (((num-j)%k)==0)
- {
- flag=1;
- i=(num-j)/k;
- }
- if (flag==1)
- {
- printf("%I64d = ",num);
- for (t=0;t<k;t++)
- {
- printf("%I64d",i+t);
- if ((t+1)<k)
- {
- printf(" + ");
- }
- }
- flag=0;
- cout<<endl;
- }
- if ((k+1)%2==0)
- {
- j=((k+1)/2)*k;
- }
- else
- {
- j=(k/2)*(k+1);
- }
- }
- if (flag==-1)
- {
- printf("%I64d不可以表示成连续的自然数\n",num);
- }
- }
- void main()
- {
- __int64 num;
- cout<<"请输入一个64位正整数:"<<endl;
- //cin>>num; 编译出错,cin适合32位的
- scanf("%I64d",&num);
- AddNum(num);
- }

第三题
设64位数中最大的子序列数位X。有k个子序列。
则X=1+2+3+。。。。+K=K*(1+K)/2
8位数:k*(k+1)/2 <0xFF 得到方程: k^2 + k -512 < 0 ,解方程得 k <22.13. 取k=22. 从1+2+。。。+22就可以得到想要得到的数。
对于64位的数。同样利用上面的方程:k*(k+1)/2 <0xFFFFFFFFFFFFFFFF 得到方程: k^2 + k - (2*0xFFFFFFFFFFFFFFFF) < 0.
解方程得到: k <=6074000999 则num= 18446744070963499500
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
问题一解法:双指针遍历
这题有两种解法, 其中一种便是双指针法,还有一种比较巧妙,利用了数学方法,简单来说是求出一个公式来。这里只说双指针的解法。
这里需要一个转化,把求n中所有可能的连续自然数之和归约为在数组{1,2,3,...,n}中找所有连续子序列和等于n的问题。这里同样也是这样一个场景:对有序数组如何遍历来求得符合要求的数据集合?这时的双指针可以不是一头一尾了,而是两个都指向头部,这样可以以高效的顺序遍历我们要找的所有集合。初始设i=j=1,这里同样会出现三种情况:
-
sum[i,j] == sum, 直接输出i到j的值,并把i+1,j+1,因为只是i+1肯定是不等的,因为和小了,同样j+1只会使和变大,所以两个都要往前加(注意这里指针不用考虑减小,因为这在以前就考虑过了)
-
sum[i,j] < sum,说明偏小,那么提高j来使得和变大才有可能相等
-
sum[i,j] > sum,说明偏大,那么提高i来使得和变小才有可能相等
-
这样,代码就出来了:
public static void GetAnswer(int n) { int i =0, j = 0; while (i <= (n / 2) && j <= n) { int sum = (j + i)*(j - i + 1) / 2; if (sum == n) { for (int k = i; k <= j; k++) Console.WriteLine(k); i++; j++; } else if (sum < n) //sum[i..j]<n,只能提高j以增大sum { j++; } else //sum[i..j]>n,只能提高i以减小sum { i ++; } } }
所谓双指针,是利用两个指针对一个有序数组进行遍历,查找出符合要求的数据集合。相信大家都接触到了这种思维模式的解题方法,只是没有注意到罢了。下面举几个例子吧。
例1:给定一个数组a[n],求数组中是否存在两个数的和等于给定值sum并输出?
这个问题很常见,我当年在面试微软实习生的时候就被问到了此题,解决方法有很多种,这里我就不赘述,我讲的是用双指针遍历法的。首先数组不一定有序,对数组排序是必须的。那么便来到了这样一个场景:对有序数组如何遍历来求得符合要求的数据集合?双指针的解决方法如下:定义两个指针(i 和 j),分别指向数组头和尾,那么会出现如下三种情况:
-
如果a[i]+a[j] == sum,那么很显然,只要输出这两个数,并把指针i+1和j-1指向下一个数即可。(这里不输出重复的组合)
-
如果a[i]+a[j] > sum,说明当前遍历的数值偏大,所以可以把j-1以减小和的值,在继续比较。
-
如果a[i]+a[j] < sum,说明当前遍历的数值偏小,同样为了加大和可以把i+1。
-
总的时间复杂度取决于排序即O(nlogn)。
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------分析:假设可以写成连续i个自然数之和,假设这个序列第一个自然数为j,即为j , j+1,j+2,j+3...j+i-1,这个序列为等差数列,和为i[(i-1)/2+j]
即数n要表示成i[(i-1)/2+j]的形式。首先要判断(n-i*(i-1)/2)%i==0,i*(i-1)/2肯定可以整除,因为i至少为2,i*(i-1)/2用计算机求解与实际值相同,因为i*(i-1)为偶数。若成立则可以表示成连续的自然数之和。
j可以通过j=(n-i*(i-1)/2)/i求解
代码如下:
- #include <iostream>
- using namespace std;
- void conAdd(int n)
- {
- int j;
- bool flag=false;
- for(int i=2;n>i*(i-1)/2;i++)
- {
- //判断是否可以表示成连续的自然数
- if((n-i*(i-1)/2)%i==0)
- {
- flag=true;
- j=(n-i*(i-1)/2)/i;
- for(int k=0;k<i-1;k++)
- cout<<j+k<<"+";
- cout<<j+i-1;
- cout<<"="<<n;
- cout<<endl;
- }
- }
- if(!flag)
- cout<<"the integer "<<n<<" "<<"can not be added by continuous natural number"<<endl;
- }
- int main()
- {
- int i=9;
- conAdd(i);
- i=18;
- conAdd(i);
- conAdd(8);
- conAdd(11);
- cin>>i;
- return 0;
- }








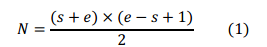
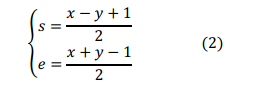















 2977
2977











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








