CF 449E Jzzhu and Squares解题报告

本文链接：https://blog.csdn.net/wmdcstdio/article/details/52734145

题目大意

http://codeforces.com/contest/449/problem/E

给定一个N*M的网格。对一个顶点为格点的正方形R（不一定与格线平行），计算出其中有多少个单位格被R完全包含（记作F(R)）。求所有正方形的F(R)之和。

题解

首先画一个“勾股图”：

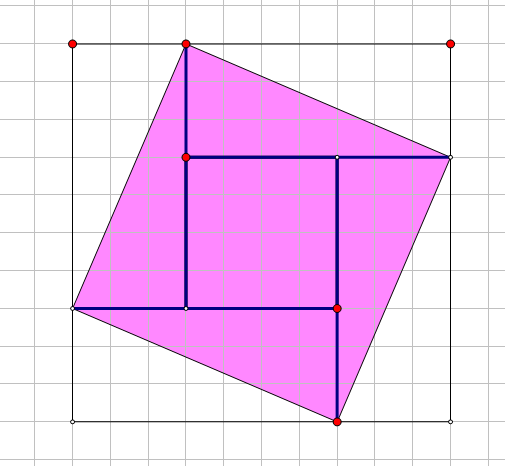
粉色是我们的正方形（不和格线平行），设其外接正方形的边长为L，四周直角三角形的短边为a，则长边为L-a。设其中完整包含了F(L,a)个单位格。

可以发现，其中完全包含的单位正方形分成两部分：第一部分是中间小正方形里的 $(L-2a)^2$ 个，第二部分是周边直角三角形里包含的。

我们这么计算第二部分：一红一白两个直角三角形拼成的矩形内有(L-a)*a个单位格，而对角线穿过了L-gcd(L,a)格，再除以2，就得到了一个三角形内的单位格数。将其乘以4，总共加起来得到：

$F(L,a)= (L-2a)^2+2[a(L-a)-L+gcd(L,a)]$

没错，“斜线下方的格点数”没有简单公式，但“单位格数”有！

可以发现，F(L,a)即使当a>L-a时也成立，所以我们可以直接用a枚举到底，整道题目的答案就是：

$\sum_{L=1}^{min(N,M)}\right\left ( N+1-L \right )\left (M+1-L)\right\sum_{a=1}^{L}{F\left(L,a \right ) }$

我们把 $\sum_{a=1}^{L}F(L,a)$ 展开：

$\sum_{a=1}^{L}F(L,a) = L(L^2-2L)-L(L+1)L+\frac{1}{3}L(L+1)(2L+1)+2\sum_{a=1}^{L}gcd(L,a)\\=\frac{1}{3}L(L+1)(2L+1)-3L^2+2\sum_{a=1}^{L}gcd(L,a)$

这分成两部分：第一部分是一个关于L的多项式，第二部分是gcd(L,a)的前缀和。

可以想象， $(N+1-L)(M+1-L)\sum_{a=1}^{L}F(L,a)$ 也是如此分成两部分：第一部分是一个关于L的多项式（确切地说，是5次多项式），第二部分也是一个关于L的“多项式”，但其“未知数项”不是 $L^i$ 这种形式，而是 $L^i\cdot \sum_{a=1}^{L}gcd(a,L)$ 这种形式。

至于怎么得到这个多项式呢，如果你数学好可以手推……作为一名数学技能荒废一年的咸鱼选手，我就直接用vector当低配版多项式类，让电脑推了……

不要忘了，我们要求的是上面那个玩意的前缀和。因此，只需要求出来 $L^i$ 和 $L^i\cdot \sum_{a=1}^{L}gcd(a,L)$ 这两种形式关于L的“前缀和”，然后乘以多项式中相应的系数，就可以完成任务。

前者很简单：L不超过10^6，暴力递推即可。后者也差不多，只需要先递推出来phi函数，然后枚举gcd(a,L)的值，就可以把Σgcd的表都打出来，详见代码。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
typedef long long LL;
typedef vector<LL> Poly;
const LL MOD=1000000007;
const int H=6;
LL gcd(LL a,LL b){
	return !b?a:gcd(b,a%b);
}
LL lcm(LL a,LL b){
	return a*b/gcd(a,b);
}
LL quickpow(LL a,LL n){
	LL ans=1;
	while(n){
		if(n&1) ans=(ans*a)%MOD;
		a=(a*a)%MOD;
		n>>=1;
	}
	return ans;
}
LL inverse(LL a){
	return quickpow(a,MOD-2);
}
void print(Poly a){
	for(int i=0;i<a.size();i++){cout<<a[i]<<" ";}cout<<endl;
}
Poly operator * (Poly a,LL b){
	for(int i=0;i<a.size();i++){
		a[i]*=b;
		a[i]%=MOD;
	}
	return a;
}
Poly operator / (Poly a,LL b){
	return a*inverse(b);
}
Poly operator + (Poly a,Poly b){
	Poly c;
	int n=max(a.size(),b.size());
	c.resize(n);
	for(int i=0;i<a.size();i++){
		c[i]+=a[i];
		c[i]%=MOD;
	}
	for(int i=0;i<b.size();i++){
		c[i]+=b[i];
		c[i]%=MOD;
	}
	return c;
}
Poly operator * (Poly a,Poly b){
	Poly c;
	c.resize(a.size()+b.size()-1);
	for(int i=0;i<a.size();i++){
		for(int j=0;j<b.size();j++){
			c[i+j]+=a[i]*b[j]%MOD;
			c[i+j]%=MOD;
		}
	}
	return c;
}
const int SIZEN=1000010;
LL calc_presum_with(Poly a,LL ps[]){
	LL ans=0;
	for(int i=0;i<a.size();i++){
		ans+=(a[i]*ps[i])%MOD;
		ans%=MOD;
	}
	return ans;
}
Poly give_Fsum_L(void){//the component without gcd
	static LL A[10];
	A[0]=1;Poly ans(A,A+1);
	A[0]=0,A[1]=1;ans=ans*Poly(A,A+2);
	A[0]=1,A[1]=1;ans=ans*Poly(A,A+2);
	A[0]=1,A[1]=2;ans=ans*Poly(A,A+2);
	ans=ans/3;
	A[0]=0,A[1]=0,A[2]=-3;ans=ans+Poly(A,A+3);
	return ans;
}
LL G[SIZEN]={0};
LL phi[SIZEN];
LL P[SIZEN][H],PG[SIZEN][H];
void work(LL N,LL M){
	static LL A[10]; 
	if(N>M) swap(N,M);
	//N是较小者
	A[0]=M+1,A[1]=-1;Poly D(A,A+2);
	A[0]=N+1,A[1]=-1;D=D*Poly(A,A+2);
	Poly F=give_Fsum_L();
	Poly F1=D*F;
	LL ans=0;
	ans+=calc_presum_with(F1,P[N]);
	ans%=MOD;
	A[0]=2;
	Poly F2=D*Poly(A,A+1);
	ans+=calc_presum_with(F2,PG[N]);
	ans%=MOD;
	ans=(ans+MOD)%MOD;
	printf("%I64d\n",ans);
}
void prepare(void){
	for(int i=1;i<SIZEN;i++){//精妙的求phi方法 
		phi[i]+=i;
		for(int j=i+i;j<SIZEN;j+=i){
			phi[j]-=phi[i];
		}
	}
	for(int g=1;g<SIZEN;g++){//求gcd(x,i)的前缀和 
		G[g]+=g;
		G[g]%=MOD;
		for(int x=2*g,d=2;x<SIZEN;x+=g,d++){
			G[x]+=(g*phi[d]%MOD);
			G[x]%=MOD;
		}
	}
	for(int i=0;i<H;i++){P[0][i]=PG[0][i]=0;}
	for(LL x=1;x<SIZEN;x++){
		LL p=1;
		for(int i=0;i<H;i++){
			P[x][i]=(P[x-1][i]+p)%MOD;
			PG[x][i]=(PG[x-1][i]+(p*G[x])%MOD)%MOD;
			p=(p*x)%MOD;
		}
	}
}
int main(){
	prepare();
	LL T,N,M;
	scanf("%I64d",&T);
	while(T--){
		scanf("%I64d%I64d",&N,&M);
		work(N,M);
	}
	return 0;
}