并查集进阶

最新推荐文章于 2023-05-20 21:10:32 发布

大漠知秋

最新推荐文章于 2023-05-20 21:10:32 发布

阅读量500

点赞数

分类专栏：数据结构与算法 C++ 文章标签：数据结构算法 c++

本文链接：https://blog.csdn.net/wo18237095579/article/details/125651249

版权

数据结构与算法同时被 2 个专栏收录

10 篇文章 0 订阅

订阅专栏

C++

10 篇文章 0 订阅

订阅专栏

作用

并查集可以快速度的解决连接问题，比如 A 和 B 是否相连。比如下图：

问红色的两个点是否相连，毫无疑问，一眼就看出来，是相连的。

问绿色的两个点是否相连，可能就需要看一会了，才能观察出来是否相连，如果更多，那可能就无法观察出来了，所以就引出了并查集这种数据结构。

同时，他也可以用在人与人关系中，比如社交网络，每个人就相当于一个点。计算机网络，每台计算机点等等。

并查集可以解决两点是否连接的问题，但是无法提供详细的连接路径。相当于只关心两者是否认识，而不关心两者是通过介绍认识或者通过网络认识等等。有失就有得，既然不用关心中间的路径，那相对来说此数据结构的效率就会更高。

并查集这种数据结构操作并不复杂，一般包括两种操作：

Find：查找一个点属于哪个组
Union：把两个点合并到一个组中

结构

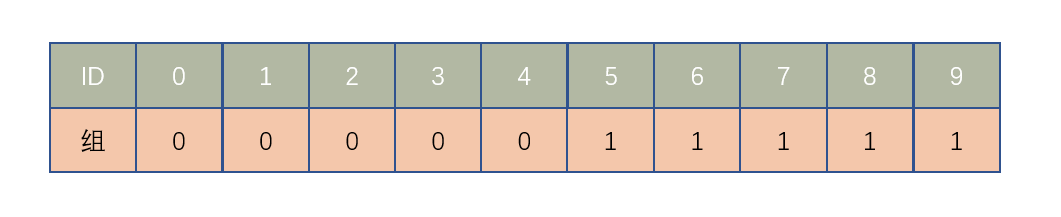
上图可以表示为 0、1、2、3、4 都属于组 0，5、6、7、8、9 都属于组 1，也可以说他们相连。当然，也可以把 0、2、4、6、8 这些偶数划分到一组里，这就看具体业务了。通过图上的结构也可看出，在一般的简单实现中可以采用数组的方式进行表示。

Quick Find

快速查询的方式特点是简单、便于理解、查询速度很快，可以达到 O(1) 级别，但是合并的速度慢。

实现

#include <iostream>
#include <cassert>

class QuickFind {
private:
    int *id;
    int count;

public:
    QuickFind(int n) {
        count = n;
        // 开辟对应数量的空间
        id = new int[n];
        // 初始化的时候，两两之间都不是一个组（不相连），所以给个默认值
        for (int i = 0; i < n; ++i) {
            id[i] = i;
        }
    }

    ~QuickFind() {
        delete[] id;
    }

    /**
     * 查找相应元素对应的组
     *
     * 时间复杂度：O(1)
     *
     * @param p 查找元素
     * @return 所在组
     */
    int find(int p) {
        assert(p >= 0 && p < count);
        return id[p];
    }

    /**
     * 判断两个元素是否在一个组（相连）
     */
    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }

    /**
     * 把元素 p 所在分组的所有元素都合并到元素 q 所在分组
     *
     * 时间复杂度：O(n)
     *
     * @param p
     * @param q
     */
    void unionElements(int p, int q) {
        int pGroup = find(p);
        int qGroup = find(q);

        if (pGroup == qGroup) {
            // 本身就是一组的，返回就行
            return;
        }

        // 找到所有原来属于 pGroup 的元素，都更改成 qGroup
        for (int i = 0; i < count; ++i) {
            if (pGroup == id[i]) {
                id[i] = qGroup;
            }
        }
    }
};

测试效率

随机测试方法，指定 n 个元素，先对 n 个元素进行随机合并分组操作，再随机抽取 n 各元素判断是否相连。

void testQF(int n) {

    srand(time(NULL));
    QuickFind uf = QuickFind(n);

    time_t startTime = clock();

    // 进行 n 次操作, 每次随机选择两个元素进行合并操作
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        uf.unionElements(a, b);
    }
    // 再进行n次操作, 每次随机选择两个元素, 查询他们是否同属一个集合
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        uf.isConnected(a, b);
    }
    time_t endTime = clock();

    // 打印输出对这2n个操作的耗时
    std::cout << "QF 2n: " << 2 * n << " ops: " << double(endTime - startTime) / CLOCKS_PER_SEC << "s" << std::endl;
}

int main() {
    std::cout << "QuickFind START" << std::endl;
    std::cout << "QuickFind 10000: ";
    testQF(10000);
    std::cout << "QuickFind 100000: ";
    testQF(100000);
    std::cout << "QuickFind 1000000: ";
    testQF(1000000);
    std::cout << "QuickFind END" << std::endl;

    return 0;
}

结果:

QuickFind START
QuickFind 10000: QF 2n: 20000 ops: 0.091s
QuickFind 100000: QF 2n: 200000 ops: 3.524s
QuickFind 1000000: QF 2n: 2000000 ops: 33.375s
QuickFind END

当数据量达到 10W 时，已经需要耗费 3.524 秒了，这个效率已经有点不太理想了，可以分析下性能耗费在哪里。isConnected 里面调用的是 find，find 的时间复杂度为 O(1)，不存在性能问题。再看 unionElements，测试方法里面循环了一个 n。

for (int i = 0; i < n; i++) {
    int a = rand() % n;
    int b = rand() % n;
    uf.unionElements(a, b);
}

而 unionElements 方法本身就是 O(n) 的时间复杂度，那综合来看就是 O(n^2) 的时间复杂度，性能消耗就在此处。

Quick Union

说明

为了解决合并时间复杂度过高的问题，就引出了 Quick Union 的概念。

每个元素都指向一个父元素，父元素再指向父元素的父元素，依次向上，最顶部的元素就没有父元素了，那么指向其自身，那最顶部的元素就是所属的组，这样就形成了一个树结构。

假设有 7、5、1 三个元素，初始情况父元素都是指向自己，先把 1 合并到 5，再把 5 合并到 7。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-f1g9f2K2-1657152996899)(http://pencil.file.lynchj.com/depend/20220616192040.gif)]

假设现在有一个新的元素 2 要合并到已存在 1 或者 5 或者 7 上，那么就需要把 2 的父元素指向 1 或者 5 或者 7 的根元素，1、5、7 的根元素都是 7，也就是最终 2 的父元素指向了 7。

Quick Union

假设有一个已存在的元素节点树，其根节点为 6，要合并到 1 上，最终会指向到 1 的根节点 7。

Quick Union

假设是让 3 合并到 1，最终结果也是一样的，也是 6 的父节点指向 7。

总结来说就是，把 A 节点合并到 B 节点，需要把 A 根节点的父元素指向 B 的根节点。一个比较完整的动画演示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LowBOiiZ-1657152996900)(http://pencil.file.lynchj.com/depend/20220616224316.gif)]

Quick Union 的实现如果想要判断两个点是否相连，就没有 Quick Find 那么方便，需要判断两点的根节点是否是同一个。而让两点相连就会快速很多，不用每次都要遍历整个 n。

上图中，Union 7 To 3 这一步，也可以做成把 5 的父元素节点设置成 3，那为什么要指向 4 呢，假设指向了 3，那这种逻辑下势必会让整个树层级快速的变高，而判断两点是否相连是需要查找两点的根节点是否相同，树的层级越高，相对来说找到根节点肯定就越慢，这里直接指向 4 算是一个小优化。

实现

#include <iostream>
#include <cassert>

class QuickUnion {
private:
    int *parent;
    int count;

public:
    QuickUnion(int n) {
        count = n;
        // 开辟对应数量的空间
        parent = new int[n];
        // 初始化的时候，两两之间都不是一个组（不相连），所以给个默认值
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
        }
    }

    ~QuickUnion() {
        delete[] parent;
    }

    /**
     * 查找相应元素对应的组
     *
     * 时间复杂度：O(h)，h 为树的高度
     *
     * @param p 查找元素
     * @return 所在组
     */
    int find(int p) {
        assert(p >= 0 && p < count);
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    /**
     * 判断两个元素是否在一个组（相连）
     *
     * 时间复杂度：O(h)，h 为树的高度
     */
    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }

    /**
     * 把元素 p 所在分组的所有元素都合并到元素 q 所在分组
     *
     * 时间复杂度：O(h)，h 为树的高度
     *
     * @param p
     * @param q
     */
    void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);

        if (pRoot == qRoot) {
            // 本身就是一组的，返回就行
            return;
        }

        // 直接把 p 的根元素节点的父元素指向 q 根元素节点即可
        parent[pRoot] = qRoot;
    }
};

测试效率

void testQU(int n) {

    srand(time(NULL));
    QuickUnion qu = QuickUnion(n);

    time_t startTime = clock();

    // 进行 n 次操作, 每次随机选择两个元素进行合并操作
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        qu.unionElements(a, b);
    }
    // 再进行n次操作, 每次随机选择两个元素, 查询他们是否同属一个集合
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        qu.isConnected(a, b);
    }
    time_t endTime = clock();

    // 打印输出对这2n个操作的耗时
    std::cout << "QU 2n: " << 2 * n << " ops: " << double(endTime - startTime) / CLOCKS_PER_SEC << "s" << std::endl;
}

int main() {
    std::cout << "QuickUnion START" << std::endl;
    std::cout << "QuickUnion 10000: ";
    testQU(10000);
    std::cout << "QuickUnion 100000: ";
    testQU(100000);
    std::cout << "QuickUnion 1000000: ";
    testQU(1000000);
    std::cout << "QuickUnion END" << std::endl;

    return 0;
}

结果：

QuickUnion START
QuickUnion 10000: QU 2n: 20000 ops: 0.032s
QuickUnion 100000: QU 2n: 200000 ops: 4.067s
QuickUnion 1000000: QU 2n: 2000000 ops: 51.655s
QuickUnion END

通过与上边的 Quick Find 对比发现，慢的不是一点半点。原因分析如下表：

时间复杂度统计	Quick Find	Quick Union
find	O(1)	O(h, h 为树的高度)
isConnected	O(1)	O(h)
unionElements	O(n)	o(h)

总的来看，当 h 的高度越高时，Quick Union 的时间消耗就会越多。

Size 优化

说明

已知的结果是 Quick Union 中 h 越高，时间消耗就越多，先观察下面的一个合并过程：

Quick Union 合并

这和之前的逻辑没有什么区别，把元素 7 合并到元素 6，就找到 7 的根元素节点的父节点设置成 6 的根元素节点即可。这样的结果就是树的高度变高了，而树的高度越高，Quick Union 的效率就越低。可以增加一个 Size，其作用就是在合并时，把树高度比较低的合并到树高度比较高的上，比如下：

Quick Union 基于 Size 的合并

经过这么一调整，树的高度没有变高，这一改动会更好的控制树的高度，使后续的 find 等操作更快一点。

实现



#include <iostream>
#include <cassert>

class QuickUnionSize {
private:
    int *parent;
    /**
     * sz[i]: 表示以 i 为根的这棵树中有多少个元素。
     */
    int *sz;
    int count;

public:
    QuickUnionSize(int n) {
        count = n;
        // 开辟对应数量的空间
        parent = new int[n];
        sz = new int[n];
        // 初始化的时候，两两之间都不是一个组（不相连），所以给个默认值
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
            sz[i] = 1;
        }
    }

    ~QuickUnionSize() {
        delete[] parent;
        delete[] sz;
    }

    /**
     * 查找相应元素对应的组
     *
     * 时间复杂度：O(h)，h 为树的高度
     *
     * @param p 查找元素
     * @return 所在组
     */
    int find(int p) {
        assert(p >= 0 && p < count);
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    /**
     * 判断两个元素是否在一个组（相连）
     *
     * 时间复杂度：O(h)，h 为树的高度
     */
    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }

    /**
     * 把元素 p 所在分组的所有元素都合并到元素 q 所在分组
     *
     * 时间复杂度：O(h)，h 为树的高度
     *
     * @param p
     * @param q
     */
    void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);

        if (pRoot == qRoot) {
            // 本身就是一组的，返回就行
            return;
        }

        if (sz[pRoot] < sz[qRoot]) {
            // p 节点这个树的高度 小于 q 节点这个树
            // 所以要把 pRoot 的父节点指向 qRoot，并且 qRoot 的 Size 要加上 pRoot 的 Size
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        } else {
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
};

测试效率

void testQUS(int n) {

    srand(time(NULL));
    QuickUnionSize qus = QuickUnionSize(n);

    time_t startTime = clock();

    // 进行 n 次操作, 每次随机选择两个元素进行合并操作
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        qus.unionElements(a, b);
    }
    // 再进行n次操作, 每次随机选择两个元素, 查询他们是否同属一个集合
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        qus.isConnected(a, b);
    }
    time_t endTime = clock();

    // 打印输出对这2n个操作的耗时
    std::cout << "QUS 2n: " << 2 * n << " ops: " << double(endTime - startTime) / CLOCKS_PER_SEC << "s" << std::endl;
}

int main() {
    std::cout << "QuickUnionSize START" << std::endl;
    std::cout << "QuickUnionSize 10000: ";
    testQUS(10000);
    std::cout << "QuickUnionSize 100000: ";
    testQUS(100000);
    std::cout << "QuickUnionSize 1000000: ";
    testQUS(1000000);
    std::cout << "QuickUnionSize END" << std::endl;

    return 0;
}

结果：

QuickUnionSize START
QuickUnionSize 10000: QUS 2n: 20000 ops: 0s
QuickUnionSize 100000: QUS 2n: 200000 ops: 0.01s
QuickUnionSize 1000000: QUS 2n: 2000000 ops: 0.104s
QuickUnionSize END

可以说是很喜人了。

注意：Size 代表的是一棵树存在多少个元素（一棵树的所有分支都计算在内），而不是代表其最大的 h。

Rank

说明

Size 的方式其实是一种不算公平的方式，看下图：

不公平的 Size

这是由于根元素节点 4 其 Size 大小为 5，而根元素节点 5，其 Size 大小为 3，数量少的合并到数量多的，所以就把 5 的父节点指向了 4。从图中也能看出来，以 4 为根节点的这棵树，高度最高也就 2，而以 5 为根节点的这棵树，高度最高是 3，而在 Quick Union 这种数据结构中，高度(h)肯定是越小越好。Rank 的作用就是用一棵树最高的层级作比较，而不是像 Size 那样，比较树中拥有的元素总数。

实现

#include <iostream>
#include <cassert>

class QuickUnionRank {
private:
    int *parent;
    /**
     * rank[i]: 表示以 i 为根的这棵树中最大的 h。
     */
    int *rank;
    int count;

public:
    QuickUnionRank(int n) {
        count = n;
        // 开辟对应数量的空间
        parent = new int[n];
        rank = new int[n];
        // 初始化的时候，两两之间都不是一个组（不相连），所以给个默认值
        for (int i = 0; i < n; ++i) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    ~QuickUnionRank() {
        delete[] parent;
        delete[] rank;
    }

    /**
     * 查找相应元素对应的组
     *
     * 时间复杂度：O(h)，h 为树的高度
     *
     * @param p 查找元素
     * @return 所在组
     */
    int find(int p) {
        assert(p >= 0 && p < count);
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    /**
     * 判断两个元素是否在一个组（相连）
     *
     * 时间复杂度：O(h)，h 为树的高度
     */
    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }

    /**
     * 把元素 p 所在分组的所有元素都合并到元素 q 所在分组
     *
     * 时间复杂度：O(h)，h 为树的高度
     *
     * @param p
     * @param q
     */
    void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);

        if (pRoot == qRoot) {
            // 本身就是一组的，返回就行
            return;
        }

        if (rank[pRoot] < rank[qRoot]) {
            // pRoot 小于 qRoot，那直接指向 qRoot 就行了，qRoot 的 h 也不需要增加
            parent[pRoot] = qRoot;
        } else if (rank[qRoot] < rank[pRoot]) {
            // qRoot 小于 pRoot，那直接指向 pRoot 就行了，pRoot 的 h 也不需要增加
            parent[qRoot] = pRoot;
        } else {
            // 此时两方都相等，那谁指向谁都无所谓，被指向的一方 +1 即可。
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;
        }
    }
};

测试效率

void testQUR(int n) {

    srand(time(NULL));
    QuickUnionRank qur = QuickUnionRank(n);

    time_t startTime = clock();

    // 进行 n 次操作, 每次随机选择两个元素进行合并操作
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        qur.unionElements(a, b);
    }
    // 再进行n次操作, 每次随机选择两个元素, 查询他们是否同属一个集合
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        qur.isConnected(a, b);
    }
    time_t endTime = clock();

    // 打印输出对这2n个操作的耗时
    std::cout << "QUR 2n: " << 2 * n << " ops: " << double(endTime - startTime) / CLOCKS_PER_SEC << "s" << std::endl;
}

int main() {
    std::cout << "QuickUnionRank START" << std::endl;
    std::cout << "QuickUnionRank 10000: ";
    testQUR(10000);
    std::cout << "QuickUnionRank 100000: ";
    testQUR(100000);
    std::cout << "QuickUnionRank 1000000: ";
    testQUR(1000000);
    std::cout << "QuickUnionRank END" << std::endl;

    return 0;
}

结果：

QuickUnionRank START
QuickUnionRank 10000: QUR 2n: 20000 ops: 0s
QuickUnionRank 100000: QUR 2n: 200000 ops: 0.01s
QuickUnionRank 1000000: QUR 2n: 2000000 ops: 0.101s
QuickUnionRank END

注意：极少数情况下 Size 的算法可能会比 Rank 高，因为合并的过程中多判断了一次。Rank 的合并方式更加合理，所以普遍情况下还是效率更高。

Path Compression

说明

之前的 Size、Rank 都是在优化 union 操作，而路径压缩是在 find 阶段进行优化。假设有下面这么一棵树：

简单树

通过 find 方法查找 4 的根节点，毫无疑问，最终查找到了 0。可以拆解一下其步骤：

查找 4 的父节点是否与 4 相同。
不同，父节点是 3，继续查找 3。
查找 3 的父节点是否与 3 相同。
不同，父节点是 2，继续查找 2。
查找 2 的父节点是否与 2 相同。
不同，父节点是 1，继续查找 1。
查找 1 的父节点是否与 1 相同。
不同，父节点是 0，继续查找 0。
查找 0 的父节点是否与 0 相同。
相同，那根就是 0 。

经过一系列的循环查找，知道找到根节点，中间也没做其他操作，就是单纯的查找，其实可以多做一些压缩的操作，比如改成如下：

查找 4 的父节点是否与 4 相同。
不同，父节点是 3，把 4 的父节点修改成 3 的父节点 2。
查找 2 的父节点是否与 2 相同。
不同，父节点是 1，把 2 的父节点修改成 1 的父节点 0。
查找 0 的父节点是否与 0 相同。
相同，那根就是 0 。

动画演示如下：

压缩路径

好处有两点：

步骤变少了。
路径被压缩了，下次再查找更快了。

当压缩过程到达根时，可能会出现这种情况，父节点与自己不等，但是父节点已经是根节点了：

父节点与自己不等，但是为根

这种情况是没问题的，按照逻辑会把 1 的父节点指向父节点的父节点，那 1 的父节点的为 0，0 的父节点也是 0，所以最终 1 的父节点还是指向了 0。经过路径压缩之后树的高度 h 会被优化到只有 2 个，那 find、union、isConnected 时间复杂度近乎为 O(1)。

实现

其实改动不大，就在 find 方法中增加一行赋值代码即可。

int find(int p) {
    assert(p >= 0 && p < count);
    while (p != parent[p]) {
        // 当前查找的元素父元素与自己不相等
        // 那么就把当前元素的 父元素的父元素 设置成当前元素的父元素。相当于原来的爹变成兄弟了，爷爷变成爹了。
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;
}

测试效率

void testQUPC(int n) {

    srand(time(NULL));
    QuickUnionPathCompression qupc = QuickUnionPathCompression(n);

    time_t startTime = clock();

    // 进行 n 次操作, 每次随机选择两个元素进行合并操作
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        qupc.unionElements(a, b);
    }
    // 再进行n次操作, 每次随机选择两个元素, 查询他们是否同属一个集合
    for (int i = 0; i < n; i++) {
        int a = rand() % n;
        int b = rand() % n;
        qupc.isConnected(a, b);
    }
    time_t endTime = clock();

    // 打印输出对这2n个操作的耗时
    std::cout << "QUPC 2n: " << 2 * n << " ops: " << double(endTime - startTime) / CLOCKS_PER_SEC << "s" << std::endl;
}

int main() {
    std::cout << "QuickUnionPathCompression START" << std::endl;
    std::cout << "QuickUnionPathCompression 10000: ";
    testQUPC(10000);
    std::cout << "QuickUnionPathCompression 100000: ";
    testQUPC(100000);
    std::cout << "QuickUnionPathCompression 1000000: ";
    testQUPC(1000000);
    std::cout << "QuickUnionPathCompression END" << std::endl;

    return 0;
}

结果：

QuickUnionPathCompression START
QuickUnionPathCompression 10000: QUPC 2n: 20000 ops: 0.001s
QuickUnionPathCompression 100000: QUPC 2n: 200000 ops: 0.005s
QuickUnionPathCompression 1000000: QUPC 2n: 2000000 ops: 0.056s
QuickUnionPathCompression END

递归完全压缩路径

说明

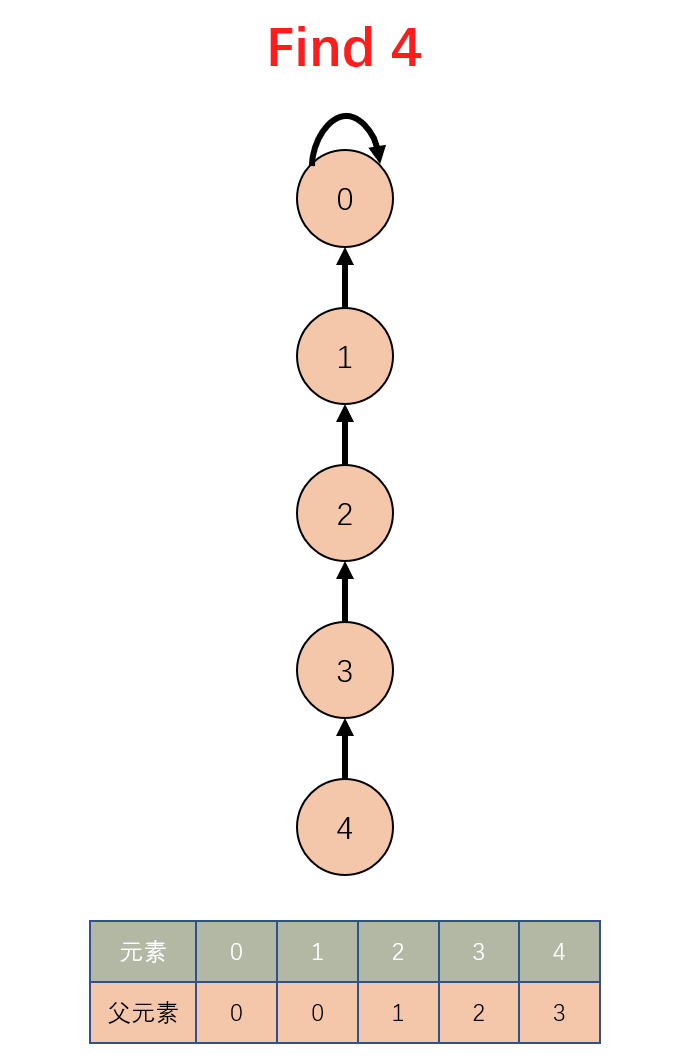
路径压缩查找 4

在上图的查找过程中，最终结果是如下：

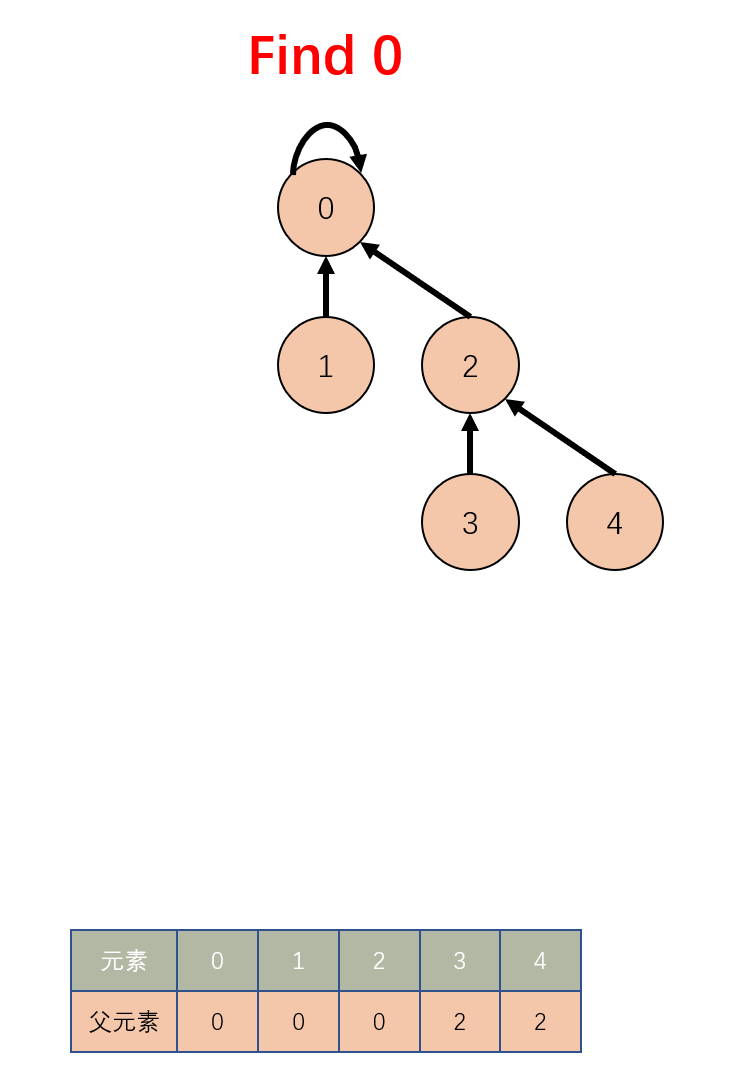
这一轮查询过后，经过路径压缩树的最高高度为 3。而最好的一种结果应该如下：

最优压缩

结果一次查找之后，能把路径全部压缩掉，让最大的高度为 2。那如何把下面这个结构通过一次查找完全压缩呢？

路径压缩查找 4

做一下推断

find(4) = 0
find(3) = 0
find(2) = 0
…

只要是在这条树上的元素，无论开始查询哪一个点，开始点以及其上所有的父节点最终都会找到根节点，当前示例，也就是 0。那也就可以写成如下递归的方式：

parent[4] = find(3); // find(3) = 0
parent[3] = find(2); // find(2) = 0
…

实现

在 find 方法中，改写成递归的方式

int find(int p) {
    assert(p >= 0 && p < count);
    /*while (p != parent[p]) {
        // 当前查找的元素父元素与自己不相等
        // 那么就把当前元素的 父元素的父元素 设置成当前元素的父元素。相当于原来的爹变成兄弟了，爷爷变成爹了。
        parent[p] = parent[parent[p]];
        p = parent[p];
    }*/

    if (p != parent[p]) {
        parent[p] = find(parent[p]);
    }
    return parent[p];
}

注意：此方式与上一步的路径压缩在效率上并没有达到质变，甚至因为递归的原因可能还会更慢。

测试效率汇总

QuickFind START
QuickFind 10000: QF 2n: 20000 ops: 0.091s
QuickFind 100000: QF 2n: 200000 ops: 3.524s
QuickFind 1000000: QF 2n: 2000000 ops: 33.375s
QuickFind END

QuickUnion START
QuickUnion 10000: QU 2n: 20000 ops: 0.032s
QuickUnion 100000: QU 2n: 200000 ops: 4.067s
QuickUnion 1000000: QU 2n: 2000000 ops: 51.655s
QuickUnion END

QuickUnionSize START
QuickUnionSize 10000: QUS 2n: 20000 ops: 0s
QuickUnionSize 100000: QUS 2n: 200000 ops: 0.01s
QuickUnionSize 1000000: QUS 2n: 2000000 ops: 0.104s
QuickUnionSize END

QuickUnionRank START
QuickUnionRank 10000: QUR 2n: 20000 ops: 0s
QuickUnionRank 100000: QUR 2n: 200000 ops: 0.01s
QuickUnionRank 1000000: QUR 2n: 2000000 ops: 0.101s
QuickUnionRank END

QuickUnionPathCompression START
QuickUnionPathCompression 10000: QUPC 2n: 20000 ops: 0.001s
QuickUnionPathCompression 100000: QUPC 2n: 200000 ops: 0.005s
QuickUnionPathCompression 1000000: QUPC 2n: 2000000 ops: 0.056s
QuickUnionPathCompression END

大漠知秋

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
并查集进阶

并查集可以快速度的解决连接问题，比如 A 和 B 是否相连。比如下图：问红色的两个点是否相连，毫无疑问，一眼就看出来，是相连的。问绿色的两个点是否相连，可能就需要看一会了，才能观察出来是否相连，如果更多，那可能就无法观察出来了，所以就引出了并查集这种数据结构。同时，他也可以用在人与人关系中，比如社交网络，每个人就相当于一个点。计算机网络，每台计算机点等等。并查集这种数据结构操作并不复杂，一般包括两种操作：上图可以表示为 0、1、2、3、4 都属于组 0，5、6、7、8、9 都属于组 1，也可以说他们相连。
复制链接

扫一扫