hdu5017 Ellipsoid（模拟退火）

最新推荐文章于 2024-09-07 15:23:19 发布

wonderzy

最新推荐文章于 2024-09-07 15:23:19 发布

阅读量869

点赞数

本文链接：https://blog.csdn.net/wondezy/article/details/39831279

版权

计算几何-三维专栏收录该内容

1 篇文章 0 订阅

订阅专栏

Ellipsoid

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1225 Accepted Submission(s): 446
Special Judge

Problem Description

Given a 3-dimension ellipsoid(椭球面)

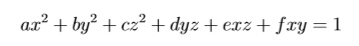
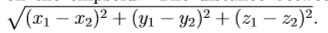
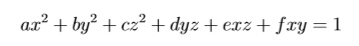
your task is to find the minimal distance between the original point (0,0,0) and points on the ellipsoid. The distance between two points (x ₁,y ₁,z ₁) and (x ₂,y ₂,z ₂) is defined as

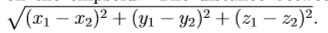
Input

There are multiple test cases. Please process till EOF.

For each testcase, one line contains 6 real number a,b,c(0 < a,b,c,< 1),d,e,f (0 ≤ d,e,f < 1), as described above. It is guaranteed that the input data forms a ellipsoid. All numbers are fit in double.

Output

For each test contains one line. Describes the minimal distance. Answer will be considered as correct if their absolute error is less than 10 ^-5.

Sample Input

  
  
   
   1 0.04 0.01 0 0 0

Sample Output

Source

2014 ACM/ICPC Asia Regional Xi'an Online

Recommend

hujie | We have carefully selected several similar problems for you: 5061 5060 5059 5058 5057

解题思路：晕，不知道怎么ac的，样例都没过。。。

#include <iostream>
#include <cstdio>
#include <time.h>
#include <cstring>
#include <cstdlib>
#include <cmath>
using namespace std;
double a,b,c,d,e,f;
double ans;
int di[8][2]={-1,0,-1,-1,0,-1,1,-1,1,1,1,0,1,-1,1};
void get_point(double x,double y){
    double len=1;
    while(len>1e-6){
        int dir=-1;
        for(int i=0;i<8;i++){
            double xx=x+len*di[i][0],yy=y+len*di[i][1];
            double A=c,B=d*yy+e*xx,C=a*xx*xx+b*yy*yy+f*xx*yy-1;
            double det=B*B-4*A*C;
            if(det<0) continue;
            double z=min((-B+sqrt(det))*(-B+sqrt(det)),(-B-sqrt(det))*(-B-sqrt(det)))/(4*A*A);
            if(xx*xx+yy*yy+z<ans){
                ans=xx*xx+yy*yy+z;
                dir=i;
            }
        }
        if(dir==-1) len/=2;
        else x+=len*di[dir][0],y+=len*di[dir][1];
    }
}
void solve(){
    ans=1e18;
    get_point(0,0);
    //get_point((rand()%10)*1.0/4/sqrt(a),(rand()%10)*1.0/4/sqrt(b));
    //get_point((rand()%10)*1.0/4/sqrt(a),-(rand()%10)*1.0/4/sqrt(b));
    //get_point(-(rand()%10)*1.0/4/sqrt(a),(rand()%10)*1.0/4/sqrt(b));
    //get_point(-(rand()%10)*1.0/4/sqrt(a),-(rand()%10)*1.0/4/sqrt(b));
    printf("%.7f\n",sqrt(ans));
}
int main(){
    while(~scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&e,&f)){
        solve();
    }
    return 0;
}
/*
0.25 -0.10 0.123 -0.234 0.456 -0.567
*/