优先队列——斐波那契堆

最新推荐文章于 2024-04-12 15:55:24 发布

woniu317

最新推荐文章于 2024-04-12 15:55:24 发布

阅读量4.4k

点赞数 1

分类专栏：算法导论文章标签：算法导论算法编程 heap

本文链接：https://blog.csdn.net/woniu317/article/details/24731207

版权

算法导论专栏收录该内容

4 篇文章 0 订阅

订阅专栏

1. 引言

最近一直在写最短路径的迪杰斯特拉与双向迪杰斯特拉算法，使用优先队列可以极大的加快算法的运行效率。比如在OL数据集中，对于迪杰斯特拉算法用优先队列（二叉堆实现）代替普通的数组（数据结构书中提供的算法）快了将近60倍。

由上可得如何实现优先队列对迪杰斯特拉、双向迪杰斯特拉以及其它用到优先队列的最短路径求解算法（如reach、A*）等至关重要。另外对于一些其他用到优先队列的问题也具有相当的影响。

对于优先队列来说，只需要入队、出队即可，因为该文章只关注堆的插入（push）与删除（delete）操作，其它操作忽略。该文中出现的队列值越小优先级越高。

几种常见的实现优先队列的堆的时间复杂度比较如表1-1所示。

表1-1 常见堆的常见操作时间复杂度比较，其中N代表结点个数

操作	二叉堆	d叉堆	左式堆	二项堆	斐波那契堆
insert	O(log₂N)	O(log_dN)	O(log₂N)	O(log₂N)	O(1)
delete	O(log₂N)	O(d*log_dN)	O(log₂N)	O(log₂N)	O(log₂N)
merge	O(n*log₂N)	O(Ndlog_dN)	O(log₂N)	O(log₂N)	O(1)
minimum	O(1)	O(1)	O(1)	O(log₂N)	O(1)
decrease-key	O(log₂N)	O(log_dN)		O(log₂N)	O(log₂N)

从理论上讲，当删除操作远远小于插入操作时，斐波那契堆是很理想的。但是，从实际上看，对于大多数应用来说，由于斐波那契堆的常数因子以及程序上设计的复杂性，使得它不如通常的二叉（或d叉）堆合适。因此斐波那契堆主要是理论上的意义。如果能设计出一种与斐波那契堆有相同的平摊时间界但又简单的数据结构，那么它就会有很大的使用价值。^[1]

2. 定义

与二项堆一样，斐波那契堆是由一组最小堆有序树构成，但堆中的树并不一定是二项树。

3. 操作

3.1 基本数据结构

斐波那契堆中的结点包含keyValue、child、leftBrother、rightBrother、parent、mark。其中，keyValue为结点的数据值，mark用于标记该结点是否失去过孩子。因为斐波那契堆中允许降低指定结点的值，并将降低值的结点提升为根，而mark标记的存在可以保证斐波那契堆中的树不至于过深（自己理解，但是不理解即使很深的话影响哪些操作）。然而对于用斐波那契堆实现优先队列，mark与parent是不需要的，因此以下操作实现中不存在mark与parent域。

斐波那契堆的属性：minH，maxDegree，cons，keyNum。其中minH指向当前堆中最小值（最高优先级）的结点，maxDegree记录了所有根结点的孩子个数的上界， cons用于辅助斐波那契堆的合并操作，keyNum记录了当前对中结点个数。

另外我采用了模板类去实现该数据结构，这样为在不同环境下使用该优先队列（斐波那契堆实现）带来了方便。

3.2 插入

插入一个结点直接将该结点加到minH后边即可。参考代码第4节中push函数。

3.3 取值

对于优先队列只需取到最小值（优先级最大）即可，而属性minH即为结果。参考代码第4节中的top函数。

3.4 删除最小值

因为在插入的时并没有对堆进行任何的调整，才使得插入操作的代价为O(1)，而在删除时需要对堆进行合并操作，即将孩子个数（degree）相同的结点合并为一棵最小堆有序树。

具体操作步骤如下：

(1) 将minH的孩子提升为根；

(2) 删除minH所指向的结点，并将其后移一个位置；

(3) 用cons（类型：fibonacci**）辅助完成堆的合并，*(cons + i)指向孩子个数为i的结点；

(4) 顺序扫描根表，并将当前结点从根表移除（不是删除）到对应的*(cons+i)中（当前结点的孩子个数为i），若*(cons+i)处已有值则合并；反之扫描下一个根，直至根表为空；

(5) 将cons中的结点串联到根表中，并将minH指向当前最小根（最小值）结点。

该部分代码实现参考了http://dsqiu.iteye.com/blog/1714961，代码实现见第4节pop()。

注意：刚开始自己实现时用了cmap，即哈希，想着这样的查找代价与空间代价可以最低。用哈希辅助实现合并操作比参考[2]的实现插入删除100000个节点足足慢了一倍。小小郁闷一下。

分析：用cmap实现忽略了(1) 合并后节点个数不会太多，比如100000个节点只需17（⌈ log₂100000⌉）个空间；(2) 两个结点孩子均为i的结点合并得到一个有i+1个孩子的结点，不需要再去哈希。用[2]中的方法，即按照上述的计算过程实现后100000个结点的插入与删除操作时间由220ms降低为78ms。

4. 代码实现

4.1 编程环境

Window 7 +vs2010

4.2 测试数据与测试结果

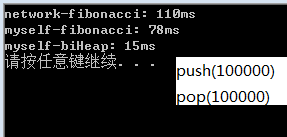
随机产生的100000个数据，首先根据二叉堆（BiHeap）^[3]的结果验证该方法实现优先队列的正确性。其次比较了与[2]、[3]进行了时间比较，时间消耗如图4-1所示。

4-1 100000个插入、删除操作运行时间对比

结果剖析：network-fibonacci代表[2]中的代码，myself-fibonacci代表用斐波那契堆实现的优先队列，myself-biHeap代表用二叉堆实现的优先队列，冒号后的数字表示运行时间。在二叉堆[3]的实现使用了静态数组，虽然插入时间复杂度高于斐波那契堆，但是因为其数组的操作简易性使得它的运行时间是最好的。另外统计表明二叉堆的插入操作平均为O(1)。

4.3 完整代码

#include "stdafx.h"
#include "testFibonacci.h"		//该文件为[2]中实现的代码，大家如果不感兴趣可以直接删除
#include "BiHeap.h"			//该文件为[3]中二叉堆实现的优先队列，大家如果不感兴趣可以直接删除

#include "afxtempl.h"
#include <assert.h>
#include <random>
#include <iostream>
using namespace std;

#define TESTNUM 100000
#define POPNUM 100000

template<class T>
class fibonacciNode
{
public:
	T keyValue;
	int degree;
	fibonacciNode *leftBrother;
	fibonacciNode *rightBrother;
	fibonacciNode *child;
	fibonacciNode()
	{
		leftBrother = this;
		rightBrother = this;
		child = NULL;
		degree = 0;
	}
	bool operator<(const fibonacciNode node)
	{
		return keyValue < node.keyValue;
	}
	bool operator<=(const fibonacciNode node)
	{
		return keyValue <= node.keyValue;
	}
	bool operator==(const fibonacciNode node)
	{
		return keyValue == node.keyValue;
	}
};

template<class T>
class CFibonacci
{
private:
	fibonacciNode<T> *minH;						//指向最小结点
	int keyNum;									//结点的个数
	int maxDegree;								//所有结点组成一棵二项树时第一层孩子结点的最大个数

private:
	void clearRecursive(fibonacciNode<T> *pCurrentNode);			//递归的释放内存空间
	inline void improveChild();					//将当前最小结点的孩子结点提升到root层
	inline void deleteMinNode();				//删除当前最小结点
	
	inline void conslidate();					//最小值出队列后，其它结点的合并
	inline fibonacciNode<T> *removeNode();		//合并操作时，用于将minH指向的结点从root队列中移除，但不delete
												//removerNode()的正确理解参考合并操作
	inline void linkNode(fibonacciNode<T> *x, fibonacciNode<T> *y);			//将树根为y的子树挂载到结点x下
	fibonacciNode<T> **cons;					//用于合并队列时指向root结点
	inline void combineCons();					//degree相同的合并为一个root并放入cons中，且此时degree+1
	inline void linkCons();						//将cons中的结点重新串联为斐波那契堆

public:
	CFibonacci();
	~CFibonacci();
	
public:
	void push(const T node);
	void pop();
	T top();
	void clear();	

};

template<class T>
CFibonacci<T>::CFibonacci()
	:minH(NULL), keyNum(0)
{
	maxDegree = int(log(TESTNUM * 1.0) / log(2.0)) + 1;
	cons = new fibonacciNode<T> *[maxDegree];
	for (int i=0; i<maxDegree; ++i)
	{
		*(cons + i) = NULL;
	}
}

template<class T>
CFibonacci<T>::~CFibonacci()
{
	if (minH)
	{
		clear();
	}
	delete []cons;
}

template<class T>
void CFibonacci<T>::push(const T node)
{
	fibonacciNode<T> *newNode = new fibonacciNode<T>;
	newNode->keyValue = node;
	keyNum ++;
	if (!minH)
	{
		minH = newNode;
		return;
	}
	newNode->leftBrother = minH;
	newNode->rightBrother = minH->rightBrother;
	minH->rightBrother->leftBrother = newNode;
	minH->rightBrother = newNode;
	if (*newNode <= *minH)
	{
		minH = newNode;
	}
}

template<class T>
void CFibonacci<T>::improveChild()
{
	fibonacciNode<T> *pCurrentNode;

	pCurrentNode = minH->child;

	fibonacciNode<T> *pTempNode;
	pTempNode = minH->rightBrother;

	pCurrentNode->rightBrother->leftBrother = minH;
	minH->rightBrother = pCurrentNode->rightBrother;

	pTempNode->leftBrother = pCurrentNode;
	pCurrentNode->rightBrother = pTempNode;
}

template<class T>
void CFibonacci<T>::deleteMinNode()
{
	fibonacciNode<T> *pCurrentNode;
	pCurrentNode = minH->rightBrother;

	minH->leftBrother->rightBrother = pCurrentNode;
	pCurrentNode->leftBrother = minH->leftBrother;

	delete minH;
	minH = pCurrentNode;
}

template<class T>
void CFibonacci<T>::pop()
{
	assert(keyNum>0);
	keyNum--;
	
	if (minH->child)
	{
		improveChild();
	}

	if (minH == minH->rightBrother)
	{
		delete minH;
		minH = NULL;
	}
	else
	{
		deleteMinNode();
		conslidate();
	}
}

template<class T>
T CFibonacci<T>::top()
{
	assert(keyNum>0);
	return minH->keyValue;
}

template<class T>
void CFibonacci<T>::clear()
{
	if (!minH)
	{
		return;
	}
	keyNum = 0;
	clearRecursive(minH);
	minH = NULL;
}

template<class T>
void CFibonacci<T>::clearRecursive(fibonacciNode<T> *pCurrentNode)
{
	fibonacciNode<T> *pCurrentRight;
	//处理孩子
	if (pCurrentNode->child)
	{
		clearRecursive(pCurrentNode->child);
		pCurrentNode->child = NULL;
	}
	//处理兄弟
	if (pCurrentNode != pCurrentNode->rightBrother)
	{
		pCurrentRight = pCurrentNode->rightBrother;
		pCurrentNode->leftBrother->rightBrother = pCurrentRight;
		pCurrentRight->leftBrother = pCurrentNode->leftBrother;
		delete pCurrentNode;
		clearRecursive(pCurrentRight);
	}
	else
	{
		delete pCurrentNode;
	}
}

template<class T>
fibonacciNode<T> *CFibonacci<T>::removeNode()
{
	fibonacciNode<T> *x = minH;
	//移除minH
	if (minH->rightBrother == minH)
	{
		minH = NULL;
	}
	else
	{
		minH->leftBrother->rightBrother = minH->rightBrother;
		minH->rightBrother->leftBrother = minH->leftBrother;
		minH = minH->rightBrother;
	}
	x->leftBrother = x;
	x->rightBrother = x;

	return x;
}

template<class T>
void CFibonacci<T>::linkNode(fibonacciNode<T> *x, fibonacciNode<T> *y)
{
	if (!x->child)
	{
		x->child = y;
	}
	else
	{
		x->child->rightBrother->leftBrother = y;
		y->rightBrother = x->child->rightBrother;

		x->child->rightBrother = y;
		y->leftBrother = x->child;
	}
	x->degree++;
}

template<class T>
void CFibonacci<T>::combineCons()
{
	fibonacciNode<T> *x, *y;
	int degree;
	while (NULL != minH)
	{
		x = removeNode();
		degree = x->degree;
		while (NULL != *(cons + degree))
		{
			y = *(cons + degree);
			if (*y < *x)
			{
				swap(x, y);
			}
			linkNode(x, y);					//将y合并为x的孩子
			*(cons + degree) = NULL;
			degree++;
		}
		*(cons + degree) = x;
	}
}

template<class T>
void CFibonacci<T>::linkCons()
{
	for (int i=0; i<maxDegree; ++i)
	{
		if (*(cons + i))
		{
			if (!minH)
			{
				minH = *(cons + i);
			}
			else
			{
				minH->rightBrother->leftBrother = *(cons + i);
				(*(cons + i))->rightBrother = minH->rightBrother;

				minH->rightBrother = *(cons + i);
				(*(cons + i))->leftBrother = minH;
				minH =*(*(cons + i)) < *minH ? (*(cons + i)):minH;
			}
			*(cons + i) = NULL;
		}
	}
}

template<class T>
void CFibonacci<T>::conslidate()
{
	//合并孩子个数相同的结点
	combineCons();

	//将cons中结点都重新加到根表中，且找出最小根
	linkCons();
}
//测斐波那契堆结果是否正确，如果不感兴趣可以直接删除
void testResult()
{
	int *arry = new int[TESTNUM];
	srand((unsigned int)time(NULL));

	for (int i=0; i<TESTNUM; ++i)
	{
		arry[i] = rand()%100;
	}

	CFibonacci<int> test;
	BiHeap<int> biHeap;

	for (int i=0; i<TESTNUM; ++i)
	{
		test.push(arry[i]);
		biHeap.push(arry[i]);
	}

	int a, b;
	for (int i=0; i<TESTNUM; ++i)
	{
		a = test.top();
		b = biHeap.top();

		if (a != b)
		{
			cout<<a<<" "<<b<<endl;
		}
		test.pop();
		biHeap.pop();
	}
	delete []arry;
}
//测斐波那契堆运行时间，如果不感兴趣可以直接删除
void testTime()
{
	//产生数据
	int *arry = new int[TESTNUM];
	srand((unsigned int)time(NULL));

	for (int i=0; i<TESTNUM; ++i)
	{
		arry[i] = rand();
	}
	DWORD start;
	
	//
	//[2]的代码运行时间测试
	FibHeap * heap = NULL;
	FibNode * x = NULL;
	start = GetTickCount();
	heap = FibHeapMake();

	FibHeapInsertKeys(heap, arry, TESTNUM);

	for (int i=0; i<POPNUM; ++i)
	{
		FibHeapExtractMin(heap);
	}

	cout<<"network-fibonacci: "<<(double)(GetTickCount() - start)<<"ms"<<endl;
	FibHeapDestory(heap);
	cout<<"//"<<endl;
	/
	//自己的斐波那契堆的运行时间测试
	CFibonacci<int> test;
	start = GetTickCount();
	for (int i=0; i<TESTNUM; ++i)
	{
		test.push(arry[i]);
	}
	for (int i=0; i<POPNUM; ++i)
	{
		test.pop();
	}
	cout<<"myself-fibonacci: "<<(double)(GetTickCount() - start)<<"ms"<<endl;
	test.clear();
	cout<<"//"<<endl;
	//
	//[3]的代码运行时间测试
	BiHeap<int> biHeap;
	start = GetTickCount();
	for (int i=0; i<TESTNUM; ++i)
	{
		biHeap.push(arry[i]);
	}

	for (int i=0; i<POPNUM; ++i)
	{
		biHeap.pop();
	}
	cout<<"myself-biHeap: "<<(double)(GetTickCount() - start)<<"ms"<<endl;
	delete []arry;
}

int _tmain(int argc, _TCHAR* argv[])
{
	testResult();
	cout<<"result correct!"<<endl;
	testTime();
	system("pause");
	return 0;
}

参考文献

[1] 算法导论

[2] http://dsqiu.iteye.com/blog/1714961

[3] http://download.csdn.net/detail/woniu317/4846336