本文深入讲解二次函数的定义、图像及性质，包括y=ax^2、y=a(x-h)^2+k和y=ax^2+bx+c等不同形式的二次函数，并探讨了a、b、c、h和k等参数对函数图像的影响。
本文目录
1. 定义
形如：
y
=
a
x
2
+
b
x
+
c
(
a
≠
0
)
y=ax^2+bx+c(a\neq0)
y=ax2+bx+c(a=0)
的函数，叫做二次函数，x是自变量，a、b、c分别是函数解析式的二次项系数、一次项系数、常数项。
2. y=ax^2图象与性质
先看下
y
=
x
2
y=x^2
y=x2
对应的图象：
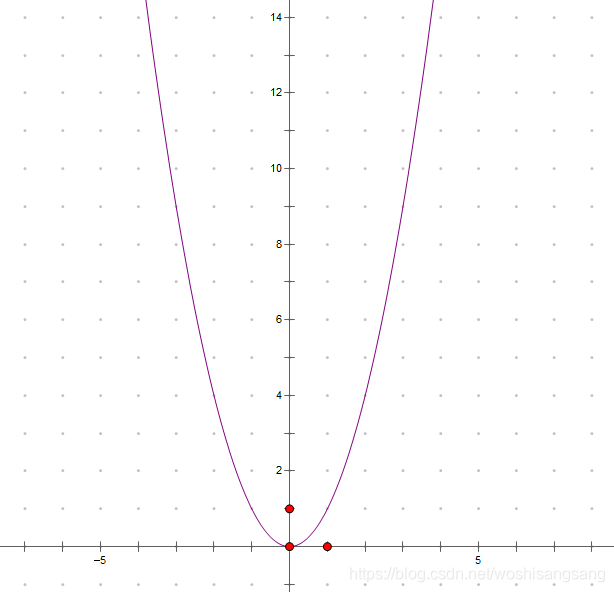
因为二次函数的形状，像是抛一个铅球时空中的轨迹(上面的图是倒过来的轨迹，想象下)，所以一般二次函数的图像可称作抛物线。
从图中可以看出，y轴是抛物线的对称轴，抛物线与它的对称轴的交点(0,0)叫做抛物线的顶点。
然后我们来看下以下几个函数的图象：
总结下规律，针对
y
=
a
x
2
y=ax^2
y=ax2
- a>0时，抛物线开口向上，a越大，抛物线开口越小。这是因为a越大，增长的越快。
- a<0时，抛物线开口往下，a越小，抛物线开口越小。a为负值时，x越大，函数值就越小。
3. y=a(x-h)^2+k图象和性质
3.1 k值对图象的影响
先来对比下以下几个函数图象：
发现，y=a(x-h)^2+k中，当k+1时，图象向上平移1个单位，k-1时，图象向下平移一个单位。
3.2 h值对图象的影响
对比图中几个函数，看下公式：
a
(
x
−
h
)
2
+
k
a(x-h)^2+k
a(x−h)2+k
h变化对图象的影响
可以发现，当h+1时，图象右移1个单位，h-1时，图象左移一个单位。
3.3 a值对图象的影响
对比图中几个函数，看下公式：
a
(
x
−
h
)
2
+
k
a(x-h)^2+k
a(x−h)2+k
a变化对图象的影响
可以看出，a的正负值影响了抛物线的开口方向，a的绝对值影响了抛物线的开口大小。
4. y=ax^2+bx+c图象与性质
通过配方法，可以将y=ax^2+bx+c转换为：
y
=
a
(
x
+
b
2
a
)
2
+
4
a
c
−
b
2
4
a
y=a{(x+\frac b{2a})}^2+\frac{4ac-b^2}{4a}
y=a(x+2ab)2+4a4ac−b2
所以推出有以下性质：
对称轴为：
x
=
−
b
2
a
x=-\frac b{2a}
x=−2ab
顶点为
(
−
b
2
a
,
4
a
c
−
b
2
4
a
)
(-\frac b{2a},\frac{4ac-b^2}{4a})
(−2ab,4a4ac−b2)
5. 二次函数与一元二次方程
这个简单，一元二次方程实际上是二次函数当y=0时的特例。
具体到图象上，一元二次方程的解就是二次函数与x轴的交点坐标值。
如下图：
扫一扫
2260
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
