昨天做了一道华为的机试题,关于RMQ。用了自己想的算法,无奈内存超了限制。
题目如下:
老师想知道从某某同学当中,分数最高的是多少,现在请你编程模拟老师的询问。当然,老师有时候需要更新某位同学的成绩.
输入描述:
输入包括多组测试数据。
每组输入第一行是两个正整数N和M(0 < N <= 30000,0 < M < 5000),分别代表学生的数目和操作的数目。
学生ID编号从1编到N。
第二行包含N个整数,代表这N个学生的初始成绩,其中第i个数代表ID为i的学生的成绩
接下来又M行,每一行有一个字符C(只取‘Q’或‘U’),和两个正整数A,B,当C为'Q'的时候, 表示这是一条询问操作,他询问ID从A到B(包括A,B)的学生当中,成绩最高的是多少
当C为‘U’的时候,表示这是一条更新操作,要求把ID为A的学生的成绩更改为B。
输出描述:
对于每一次询问操作,在一行里面输出最高成绩.
输入例子:
5 7
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 4 5
U 2 9
Q 1 5
输出例子:
5
6
5
9
我的题解如下:
#include <iostream>
#include <vector>
using namespace std;
inline int findmax(int a, int b)
{
return (a > b ? a : b);
}
void Init(int** rmq, int N)
{
int i, j;
for(i = 1; i < N; ++i)
{
for(j = 1; j <= N - i; ++j)
{
rmq[j][j + i] = findmax(rmq[j][j + i - 1], rmq[j + 1][j + i]);
}
}
}
void update(int** rmq, int id, int score, int N)
{
rmq[id][id] = score;
int i, j;
for(i = 1; i < N; ++i)
{
for(j = 1; j <= N - i; ++j)
{
rmq[j][j + i] = findmax(rmq[j][j + i - 1], rmq[j + 1][j + i]);
}
}
}
int query(int** rmq, int left, int right)
{
return rmq[left][right];
}
int main()
{
int N, M, i, score, left, right, id;
char command;
while(cin >> N >> M)
{
int** rmq = new int* [N + 1];
for(i = 0; i < N + 1; i++)
rmq[i] = new int[N + 1];
i = 1;
while(i <= N)
{
cin >> score;
rmq[i][i] = score;
i++;
}
Init(rmq, N);
while(M--)
{
cin >> command;
if(command == 'Q')
{
cin >> left >> right;
cout << query(rmq, left, right) << endl;
}
else if(command == 'U')
{
cin >> id >> score;
update(rmq, id, score, N);
}
}
}
return 0;
}解法主要使用了rmq[N+1][N+1]这个二维矩阵来存储区间最值,比如 rmq[1][4] 表示学生 id 从1到4之间的最值,而 rmq[1][1] 就简单表示学生1的成绩。算法过程形象描述如下(数字表示第i轮):
算法时间复杂度O(N^2)(指一次预处理或一次更新,其实参照题目要求的那个修改频率,时间复杂度蛮差的,在更新上还需剪枝优化),空间复杂度O(N^2),考虑到N可能很大,内存就有可能用完了。。然后。。。
然后决定学习下 Sparse Table(稀疏表)方法。
学习自:http://noalgo.info/489.html(NOALGO博客)
算法思想:
ST(Sparse Table,稀疏表)算法是求解RMQ问题的经典在线算法,以O(nlogn)时间预处理,然后在O(1)时间内回答每个查询。
ST算法本质上是动态规划算法,定义了一个二维辅助数组st[n][n],st[i][j]表示原数组a中从下标i开始,长度为2^j的子数组中的最值(以最大值为例)。注意:可以发现这样的话,空间复杂度一下减了很多!!
要求解st[i][j]时,即求下标i开始,长度为2^j的子数组的最大值时,可以把这段子数组再划分成两半,每半的长度为2^(j-1),于是前一半的最大值为st[i][j-1],后一半的最大值为st[i+2^(j-1)][j-1],于是动态规划的转移方程为:
st[i][j] = max(st[i][j-1], st[i+2^(j-1)][j-1])
现在问题是,st数组可以怎样加速我们的查询呢?
这也是算法的巧妙之处,假设求下标在u到v之间的最大值。先求u和v之间的长度len=v-u+1,然后求k=log2(len),则u到v之间的子数组可以分为两部分:
1)以u开始,长度为2^k的一段
2)以v结束,长度为2^k的一段(可以计算得到起始位置为v-2^k+1)
注意,一般情况下这两段是重叠的,但是这两段的最大值中较小的一个仍然是u到v的最大值。于是
RMQ(u,v) = max(st[u][k], st[v-2^k+1][k])核心算法如下:
const int mx = 10000 + 10; //数组最大长度
int n, a[mx]; //数组长度,数组内容
int st[mx][30]; //DP数组
void initRMQ()
{
for (int i = 0; i < n; i++) st[i][0] = a[i];
for (int j = 1; (1 << j) <= n; j++) //使用位运算加速
for (int i = 0; i + (1 << j) - 1 < n; i++)
st[i][j] = max(st[i][j-1], st[i+(1<<(j-1))][j-1]);
}
int RMQ(int u, int v)
{
int k = (int)(log(v-u+1.0) / log(2.0)); //类型转换优先级高,除法整体要加括号
return max(st[u][k], st[v-(1<<k)+1][k]);
}使用时需要先调用initRMQ()进行初始化,然后再调用RMQ(u,v)进行查询。
有时候需要得到最值的下标而不是最值内容,这时可以使用以下的下标版本:
const int mx = 10000 + 10; //数组最大长度
int n, a[mx]; //数组长度,数组内容
int st[mx][30]; //DP数组
void initRMQIndex()
{
for (int i = 0; i < n; i++) st[i][0] = i;
for (int j = 1; (1 << j) <= n; j++)
for (int i = 0; i + (1 << j) - 1 < n; i++)
st[i][j] = a[st[i][j-1]] > a[st[i+(1<<(j-1))][j-1]] ? st[i][j-1] : st[i+(1<<(j-1))][j-1];
}
int RMQIndex(int s, int v) //返回最大值的下标
{
int k = int(log(v-s+1.0) / log(2.0));
return a[st[s][k]] > a[st[v-(1<<k)+1][k]] ? st[s][k] : st[v-(1<<k)+1][k];
}
下面用此法改进之前的华为题目:
#include <iostream>
#include <math.h>
using namespace std;
#define MAXN 30010
int rmq[MAXN][30];
inline int findmax(int a, int b)
{
return (a > b ? a : b);
}
void Init(int N)
{
int i, j;
for(j = 1; (1 << j) <= N; ++j)
for(i = 1; i + (1 << j) - 1 <= N; ++i)
rmq[i][j] = findmax(rmq[i][j - 1], rmq[i + (1 << (j - 1))][j - 1]);
}
void update(int id, int score, int N)
{
rmq[id][0] = score;
int i, j;
for(j = 1; (1 << j) <= N; ++j)
for(i = 1; i + (1 << j) - 1 <= N; ++i)
rmq[i][j] = findmax(rmq[i][j - 1], rmq[i + (1 << (j - 1))][j - 1]);
}
int query(int left, int right)
{
int k = (int) (log(right - left + 1.0) / log(2.0));
return findmax(rmq[left][k], rmq[right - (1 << k) + 1][k]);
}
int main()
{
int N, M, i, score, left, right, id;
char command;
while(cin >> N >> M)
{
i = 1;
while(i <= N)
{
cin >> score;
rmq[i][0] = score;
i++;
}
Init(N);
while(M--)
{
cin >> command;
if(command == 'Q')
{
cin >> left >> right;
cout << query(left, right) << endl;
}
else if(command == 'U')
{
cin >> id >> score;
update(id, score, N);
}
}
}
return 0;
}题目样例通过,但在网上提交报Segment Fault,还没找到原因。
感觉很不爽,再找个题目验证下,hihocoder #1068 RMQ-ST算法,算法完全一样:
#include <stdio.h>
#include <math.h>
using namespace std;
#define MAXN 1000010
int rmq[MAXN][30];
inline int findmin(int a, int b)
{
return (a < b ? a : b);
}
void Init(int N)
{
int i, j;
for(j = 1; (1 << j) <= N; ++j)
for(i = 1; i + (1 << j) - 1 <= N; ++i)
rmq[i][j] = findmin(rmq[i][j - 1], rmq[i + (1 << (j - 1))][j - 1]);
}
int query(int left, int right)
{
int k = (int) (log(right - left + 1.0) / log(2.0));
return findmin(rmq[left][k], rmq[right - (1 << k) + 1][k]);
}
int main()
{
int N, Q, i, score, left, right;
scanf("%d", &N);
if(N == 0)
return 0;
i = 1;
while(i <= N)
{
scanf("%d", &score);
rmq[i][0] = score;
i++;
}
Init(N);
scanf("%d", &Q);
while(Q--)
{
scanf("%d %d", &left, &right);
printf("%d\n", query(left, right));
}
return 0;
}开始用的 cin 和 cout,结果超时了,试着用了下 scanf 和 printf ,AC!
可能的主要原因是例子中的输入输出很多,用 scanf 和 printf 能够节省不少时间。
继续往下一看,#1070 : RMQ问题再临 这个问题中涉及了修改个别点的值以及更新问题,不过该题需用到另一种数据结构线段树。
关于更新:如果是在修改 rmq[][] 后再次执行一次 Init 的操作,无疑将会超时。而事实也是这样。
线段树
这篇博文简单易懂:http://harryguo.me/2015/12/15/%E7%BA%BF%E6%AE%B5%E6%A0%91%E8%AE%B2%E8%A7%A3%E4%B8%80/(HarryGuo)
看完发现和自己最初的想法有点相似,不过线段树最重要的思想,也是我没想到的是“分治思想”
线段树使得不论是修改还是查询,时间复杂度都是O(logN)。
按照线段树的思想,做了#1070 : RMQ问题再临,时间和空间复杂度较之前的RMQ+ST都小了很多,线段树太棒了!
//1MB 26ms
#include <stdio.h>
#include <math.h>
#include <set>
using namespace std;
#define MAXN 10010
int data[MAXN];
int tree[4 * MAXN];
int N;
set<int> ans;
void pushUp(int v)
{
tree[v] = min(tree[v << 1], tree[v << 1 | 1]);
return;
}
void build(int L, int R, int v)
{
if(L == R)
{
tree[v] = data[L];
return;
}
int m = (L + R) >> 1;
build(L, m, v << 1);
build(m + 1, R, v << 1 | 1);
pushUp(v);
return;
}
void update(int id, int val, int L, int R, int v)
{
if(L == R)
{
tree[v] = val;
return;
}
int m = (L + R) >> 1;
if(id <= m)
update(id, val, L, m, v << 1);
else
update(id, val, m + 1, R, v << 1 | 1);
pushUp(v);
return;
}
void query(int left, int right, int L, int R, int v)
{
if(L >= left && R <= right)
{
ans.insert(tree[v]);
return;
}
int m = (L + R) >> 1;
if(left <= m)
query(left, right, L, m, v << 1);
if(right > m)
query(left, right, m + 1, R, v << 1 | 1);
return;
}
int main()
{
int Q, i, score, left, right;
set<int>::iterator it;
scanf("%d", &N);
if(N == 0)
return 0;
i = 1;
while(i <= N)
{
scanf("%d", &score);
data[i++] = score;
}
build(1, N, 1);
scanf("%d", &Q);
while(Q--)
{
scanf("%d %d %d", &i, &left, &right);
if(i == 0)
{
ans.clear();
query(left, right, 1, N, 1);
it = ans.begin();
printf("%d\n", *it);
}
else
update(left, right, 1, N, 1);
}
return 0;
}见识到了线段树的优点,我会在之后专门再开一贴学习线段树的用法!








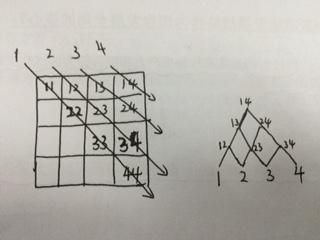














 1640
1640

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








