二叉搜索树基本知识可以看算法导论第三版163页,也可以百度搜索下,代码如下:
package com.ma.al.binaryTree;
/**
* @author xiaoma
*
*/
public class MyBinarySearchTree {
public Node root; //记录根节点
public Node current;
//===================================================================================
//为了方便就不用get/set方法了
class Node{
public Node left; //左孩子
public Node right; //右孩子
public int data; //数据
public Node(int data){
this.left = null;
this.right = null;
this.data = data;
}
}
//=====================================================================================
//增加节点
public void addNode(int data){
if(root == null){ //为空树
root =new Node(data);
}
else{
current = root;
while(current != null){ //寻找叶子节点
if(data <= current.data){
if(current.left == null){
current.left = new Node(data);
break;
}
current = current.left;
}
else{
if(current.right == null){
current.right = new Node(data);
break;
}
current = current.right;
}
}
}
}
//==========================================================================
//删除一个节点
public void delete(int data){
Node temp = root;
Node parent = root;
while(temp != null){ //寻找与data相等的项
if(data < temp.data){
if(temp.left == null){
temp = null;
System.out.println("不存在的");
break;
}
parent = temp;
temp = temp.left;
}
else if(data > temp.data){
if(temp.right == null){
temp = null;
System.out.println("不存在的");
break;
}
parent = temp;
temp = temp.right;
}
else{
break;
}
}//此时temp记录与data相等的项,parent记录temp的父节点
if(temp == null) return;//未能找到与data相等的项
if(temp == parent){//此时要删除root节点
Node temp2 = temp.right;
Node parent2 = temp.right;
while(temp2.left != null){
parent2 = temp2;
temp2 = temp2.left;
}//此时temp2记录与root的新项
if(temp2 != parent2){//root的右孩子有左孩子时
parent2.left = temp2.right;
temp2.left = root.left;
temp2.right = root.right;
root = temp2;
}
else{//root的右孩子无左孩子时
temp2.left = root.left;
temp2.right = parent2.right;
root = temp2;
}
}
else if(temp == parent.left){//要删除的项是左节点,temp记录要删除的项
if(temp.right == null && temp.left == null) parent.left = null;
else if(temp.right == null) parent.left = temp.left;
else if(temp.left == null) parent.left = temp.right;
else{
Node temp2 = temp.right;
Node parent2 = temp.right;
while(temp2.left != null){
parent2 = temp2;
temp2 = temp2.left;
}
if(temp2 != parent2){
parent2.left = temp2.right;
parent.left = temp2;
temp2.right = temp.right;
temp2.left = temp.left;
}
else{
parent.left = temp2;
temp2.left = temp.left;
temp2.right = parent2.right;
}
}
}
else{//要删除的项是右节点,temp记录要删除的项
if(temp.right == null && temp.left == null) parent.right = null;
else if(temp.right == null) parent.right = temp.left;
else if(temp.left == null) parent.right = temp.right;
else{
Node temp2 = temp.right;
Node parent2 = temp.right;
while(temp2.left != null){
parent2 = temp2;
temp2 = temp2.left;
}
if(temp2 != parent2){
parent2.left = temp2.right;
parent.right = temp2;
temp2.right = temp.right;
temp2.left = temp.left;
}
else{
parent.right = temp2;
temp2.left = temp.left;
temp2.right = parent2.right;
}
}
}
}
//==========================================================================
//中序遍历数
public void inOrderPrintTree(Node node){
if(node != null){
inOrderPrintTree(node.left);
System.out.print(node.data+",");
inOrderPrintTree(node.right);
}
}
//===========================================================================
public static void main(String[] args) {
MyBinarySearchTree my =new MyBinarySearchTree();
//下列插入顺序可以打乱
my.addNode(9);
my.addNode(5);
my.addNode(15);
my.addNode(3);
my.addNode(7);
my.addNode(11);
my.addNode(17);
my.addNode(6);
my.addNode(4);
my.addNode(1);
my.addNode(10);
my.addNode(8);
my.addNode(12);
my.addNode(16);
my.addNode(18);
my.inOrderPrintTree(my.root);//中序遍历树
System.out.println();
my.delete(9);//删除数据为9的节点
my.inOrderPrintTree(my.root);
//System.out.println(my.root.data);
}
}
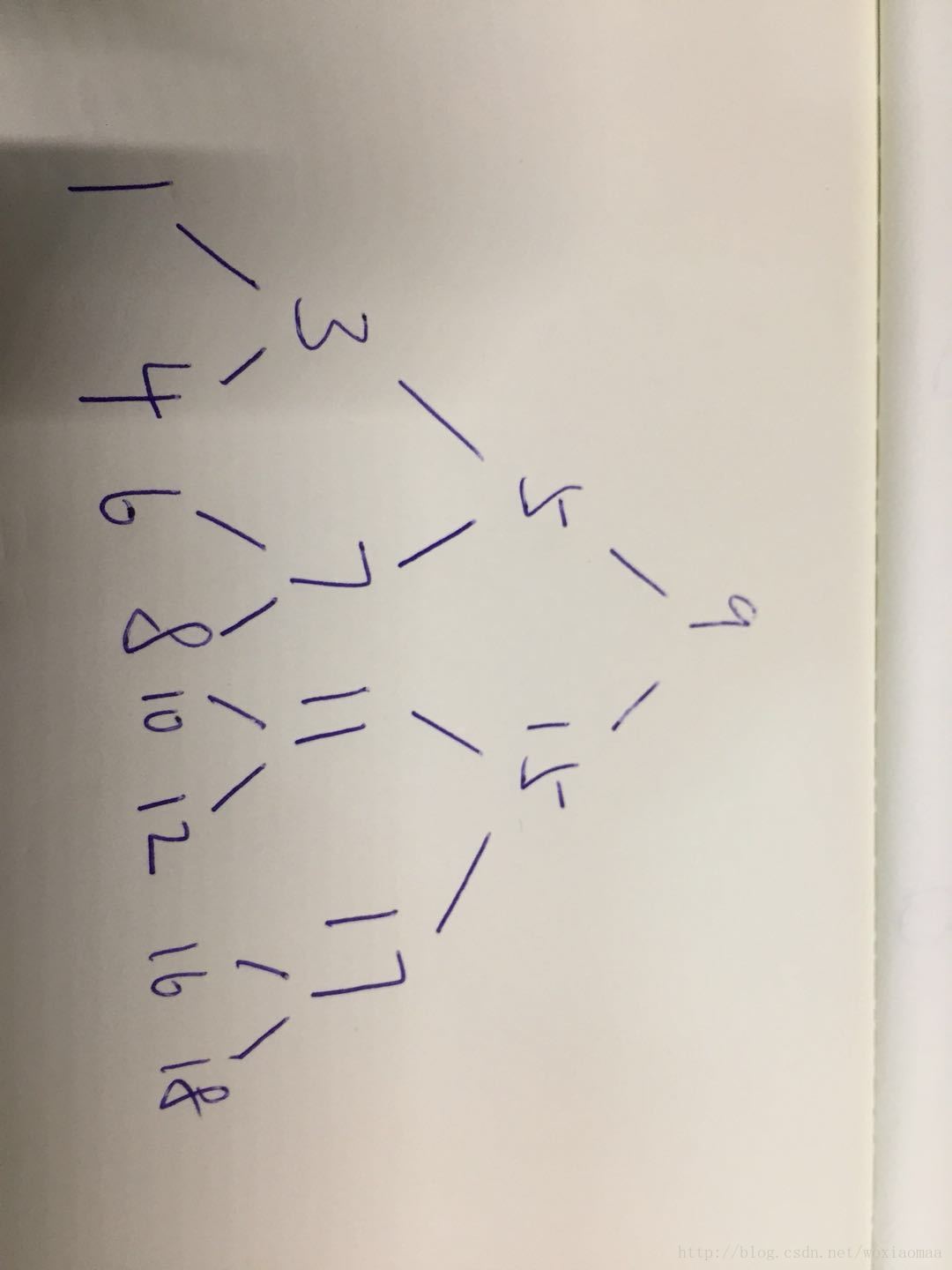
main函数构造的树如下:





















 2031
2031

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








