数据结构与算法

1、单链表
结构图:

效率问题：
时间复杂度是O(N)。平均来说，要访问一个结点，时间复杂度也有O(N/2)；

实现：
Typedef struct//表元素
{
elem *next;
结点数据
} elem;

class linkedlist//表头
{
elem *next;
};

int IsLast(elem* p)//是否是最后一个
{
return p->next==NULL;
}

elem Find(要找的数据,linkedlist* L)//Find函数
{
elem* p;
p=L->next;
while(p!=NULL&&p->结点数据!=要找的数据)
p=p->next;
}

elem PreFind(要找的数据,linkedlist* L)//找数据之前的元素
{
elem* p;
p=L->next;
while(p->next!=NULL&&p->next->结点数据!=要找的数据)
p=p->next;
}

void Delete(要删除的数据,linkedlist* L)//删除函数
{
(elem*) p,tmpcell;
p= PreFind(要删除的数据,L);
if(!IsLast(p))
{
tmpcell=p->next;
p->next=tmpcell->next;
free(tmpcell);
}
}

void Insert(要插入的数据,linkedlist* L,elem* p)//插入数据
{
elem* tmpcell;
tmpcell=malloc(sizeof(elem));
tmpcell->结点数据= 要插入的数据;
tmpcell->next=p->next;
p->next=tmpcell;
}

2、双链表:
结构图:

效率问题：
顾名思义，在双链表的结点中有两个指针，一个指向直接后继，另一个指向直接前驱,所以效率跟单链表一样

实现:
typedef struct //双链表的元素
{
elem *next;
elem *prev;
结点数据
} elem;
class linkedlist//表头
{
elem *next;
};

void Delete(要删除的数据,linkedlist* L)//删除函数
{
(elem*) p,tmpcell;
p = Find(要删除的数据,L);
if(!IsLast(p))
{
tmpcell=p->prev;
tmpcell->next=p->next;
p->next->prev=tmpcell;
free(p);
}
}

其它的变化不大

3、循环链表：
结构图:

实现：
class linkedlist//表头
{
elem *next;
elem *prev;//指向末尾
};
最后一个元素指向表头

4、栈：

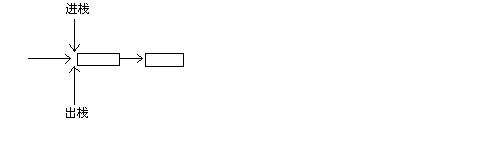
结构图：

 

实现:
由于栈是一个表，因此任何实现表的方法都可以实现栈，在这里我们运用两种流行的实现方法。
栈的链表实现：

struct Node//节点
{
数据
Node* next;
};

typdef Node* Stack;//代表栈
int IsEmpty(Stack s)//判断是否为空
{
return s->next==NULL;
}

void MakeEmpty(Stack s)//使栈为空
{
if(s==NULL)
{
error;
}
else
{
while(!IsEmpty(s))
{
pop(s);
}
}
}

Stack CreateStack()//创建栈
{
Stack s;
s=malloc(sizeof(Node));
if(!s)
{
error;
}
else
{
s->next=NULL;
MakeEmpty(s);
}
}

void Push(推入的数据,Stack s)//推入
{
Node* n;
n=malloc(sizeof(Node));
if(n==NULL)
{
error;
}
else
{
n->数据=推入的数据;
n->next=s->next;
s->next=n;
}
}

数据 Top(Stack s)//返回顶点数据
{
if(!IsEmpty(s))
{
return s->next->数据;
}
return 0;
}

void Pop(Stack s)
{
Node* n;
if(IsEmpty(s))
{
error;
}
n=s->next;
s->next=n->next;
free(n);
}

5、队列

概念：
队列是一种同栈相反和数据结构；它具有一个出口和一个入口；这是一种元素先入先出的结构;(这里我们用数组来设计一个队列)
struct Queue
{
int front;//出口
int back; //入口
int size;//目前插入的数据数
int capacity;元素数组容量
ElementData* array;
};

Queue* CreateQueue(int capacity)
{
Queue* tmpqueue;
tmpqueue=new Queue();
tmpqueue->front=0;
tmpqueue->back=0;
tmpqueue->size=0;
tmpqueue->capacity=capacity;
array=new ElementData[capacity];
}

bool IsEmpty(Queue* q)
{
if(q->size==0)
{
return true;
}
return false;
}

void Enqueue(ElementData ed,Queue* q)
{
q->array[tmpqueue->back]=ed;
q->back++;
if(q->back>q->capacity)
{
q->back=0;
}
q->size++;
}

ElementData Dequeue(Queue* q)
{
ElementData tmpdata;
if(IsEmpty(q))
{
return NULL;
}
tmpdata=q->array[q->front];
q->front++;
if(q->front>q->capacity)
{
q->front=0;
}
return tmpdata;
}

6、递归

7、二叉树

8、二叉搜索树（ADT）

概念：
对于树中的每个结点的值X，左子树的值都小于X，右子树的值都大于X；

struct TreeNode
{
数据
TreeNode* LeftNode;
TreeNode* RightNode;
}

typedef TreeNode* SearchTree;

TreeNode* FindMin(SearchTree)//搜索最小值节点
{
if(SearchTree==NULL)
{
return NULL;
}
else if(SearchTree->LeftNode!=NULL)
{
return FindMin(SearchTree->LeftNode);
}
else if(SearchTree->LeftNode==NULL)
{
return SearchTree;
}
}

TreeNode* Find(数据,SearchTree)
{
if(SearchTree==NULL)
{
return NULL;
}
if(数据<SearchTree->数据)
{
return Find(数据,SearchTree->LeftNode);
}
else if(数据>SearchTree->数据)
{
return Find(数据,SearchTree->RightNode);
}
else
{
return SearchTree;
}
}

 

TreeNode* Insert(数据,SearchTree)
{
if(SearchTree==NULL)
{
SearchTree=new SearchTree();
SearchTree->数据=数据;
SearchTree->LeftNode=SearchTree->RightNode=NULL;
}
else if(数据<SearchTree->数据)
{
SearchTree->LeftNode=Insert(数据，SearchTree->LeftNode);
}
else if(数据>SearchTree->数据)
{
SearchTree->RightNode=Insert(数据,SearchTree->RightNode);
}

return SearchTree;
}

void Delete(数据，SearchTree)
{
if(SearchTree==NULL)
{
return;
}
else if(数据<SearchTree->数据)
{
Delete(数据,SearchTree->LeftNode);
}
else if(数据>SearchTree->数据)
{
Delete(数据,SearchTree->RightNode);
}
else
{
if(SearchTree->RightNode&&SearchTree->LeftNode)//如果子树都存在，则应把右子树最小元素拿来替换（或左子树最大元素）
{
TreeNode* lptmpnode=FindMin(SearchTree->RightNode);
SearchTree->数据=lptmpnode->数据;
Delete(lptmpnode->数据,SearchTree->RightNode);
}
else//如果子树有至少一个为NULL
{
TreeNode* lptmpnode=SearchTree;
if(SearchTree->LeftNode==NULL)
{
SearchTree=SearchTree->RightNode;
}
else if(SearchTree->RightNode==NULL)
{
SearchTree=SearchTree->LeftNode;
}
free(lptmpnode);
lptmpnode==NULL;
}
}
}

9、平衡二叉树(AVL)

AVL树的特点是：
1、它本身是个二叉树；
2、每个结点的左右子树高度差的绝对值不大于1；

struct TreeNode
{
数据
int height;
TreeNode* LeftNode;
TreeNode* RightNode;
}

typedef TreeNode* SearchTree;

int Height(TreeNode* treenode)
{
if(treenode==NULL)
{
return -1;
}
else
{
return treenode->height;
}
}

//单旋转
TreeNode* LeftSingleRotate(SearchTree)
{
TreeNode* tmpnode;
tmpnode=SearchTree->LeftNode;
SearchTree->LeftNode=tmpnode->RightNode;
tmpnode->RightNode=SearchTree;
tmpnode->height=max(Height(tmpnode->LeftNode),Height(tmpnode->RightNode))+1;
SearchTree->height=max(Height(SearchTree->LeftNode),Height(SearchTree->RightNode))+1;
return tmpnode;
}
TreeNode* RightSingleRotate(SearchTree)
{
TreeNode* tmpnode;
tmpnode=SearchTree->RightNode;
SearchTree->RightNode=tmpnode->LeftNode;
tmpnode->LeftNode=SearchTree;
tmpnode->height=max(Height(tmpnode->LeftNode),Height(tmpnode->RightNode))+1;
SearchTree->height=max(Height(SearchTree->LeftNode),Height(SearchTree->RightNode))+1;
return tmpnode;
}

//双旋转
TreeNode* LeftDoubleRotate(SearchTree)
{
SearchTree->LeftNode=RightSingleRotate(SearchTree->LeftNode);
return LeftSingleRotate(SearchTree);
}
TreeNode* RightDoubleRotate(SearchTree)
{
SearchTree->RightNode=LeftSingleRotate(SearchTree->RightNode);
return RightSingleRotate(SearchTree);
}

TreeNode* Insert(数据,SearchTree)
{
if(SearchTree==NULL)
{
SearchTree=new TreeNode();
SearchTree->height=0;
SearchTree->LeftNode=SearchTree->RightNode=NULL;
}
else if(数据<SearchTree->数据)
{
SearchTree->LeftNode=Insert(数据,SearchTree->LeftNode);
if((Height(SearchTree->LeftNode)-Height(SearchTree->RightNode))==2)
{
if(数据<SearchTree->LeftNode->数据)
{
SearchTree=LeftSingleRotate(SearchTree);
}
else
{
SearchTree=LeftDoubleRotate(SearchTree);
}
}
}
else if(数据>SearchTree->数据)
{
SearchTree->RightNode=Insert(数据,SearchTree->RightNode);
if((Height(SearchTree->RightNode)-Height(SearchTree->LeftNode))==2)
{
if(数据>SearchTree->RightNode->数据)
{
SearchTree=RightSingleRotate(SearchTree);
}
else
{
SearchTree=RightDoubleRotate(SearchTree);
}
}
}
SearchTree->height=max(Height(SearchTree->LeftNode),Height(SearchTree->RightNode))+1;
return SearchTree;
}

10、优先队列

二叉堆:其实际是一棵被填满的完全二叉树;完全二叉树可以用数组表示；
对于数组中的任一位置i上的元素,它的左儿子的位置在2*i+1上,它的右儿子的位置在2*i+2上;

一棵高为h的完全二叉树，它的节点数为2^h到2^(h+1)-1个;

struct QueueHead//堆头
{
int cur_pos;//目前的位置
int capacity;//容积
ElementData* lpeledata;
}

HeapQueue* InitQueue(int nMaxEleNum)//优先队列的初始化
{
QueueHead* lptmpqueue;

lptmpqueue=new HeapQueue();

lptmpqueue->cur_pos=0;
lptmpqueue->capacity=nMaxEleNum;

lptmpqueue->lpeledata=new ElementData[nMaxEleNum];
lptmpqueue->lpeledata[0]=MinEleData;//为最小元素

return lptmpqueue(ElementData nElementData,
}

void InsertQueue(ElementData nElementData, HeapQueue* lpqueue)
{
lpqueue->cur_pos++;

int i;
for(i=lpqueue->cur_pos;lpqueue->lpeledata[i/2]>nElementData;i/=2)
{
lpqueue->lpeledata[i]=lpqueue->lpeledata[i/2];
}
lpqueue->lpeledata[i]=nElementData;
}

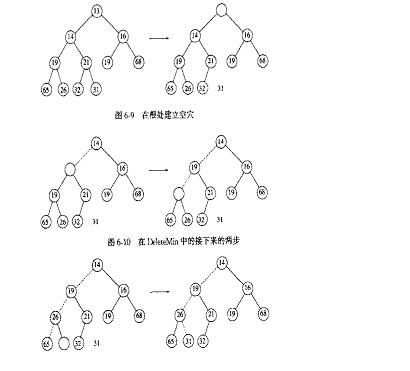
删除最小的算法可看图:

ElementData DeleteMin(HeapQueue* lpqueue)
{
ElementData tmpmin;
ElementData lastdata;
tmpmin=lpqueue->lpeledata[0];

lastdata=lpqueue->lpeledata[lpqueue->size];

lpqueue->size--;

int i=0;

while(lpqueue->lpeledata[i]<lastdata&&(2*i)<lpqueue->size)
{

if(lpqueue->lpeledata[2i+1]>lpqueue->lpeledata[2i+2])
{
lpqueue->lpeledata[i]=lpqueue->lpeledata[2i+2];
i=2i+2;
}
else
{
lpqueue->lpeledata[i]=lpqueue->lpeledata[2i+1];
i=2i+1;
}

}

lpqueue->lpeledata[i]=lastdata;
return tmpmin;
}

左式堆:

对于堆中的每个节点，左子节点的零路径长(从本节点到一个没有子节点的节点的最短路径长）大于等于右子节点的零路径长;

struct TreeNode
{
ElementData element;
TreeNode* leftNode;
TreeNode* rightNode;
int nullPathLength;//零路径长
}

typedef LeftQueue TreeNode

void SwapChildren(LeftQueue* nqueue)//把左子树同右子树互换
{
LeftQueue* tmpqueue;
tmpqueue=nqueue->leftNode;
nqueue->leftNode=nqueue->rightNode;
nqueue->rightNode=tmpqueue;
}

 

合并方法为：如果两个堆有一个为NULL，则返回另外一个堆；然后把根值小的堆的右子树同根值大的进行递归合并；由于最后合并的堆右子树会大于左子树（这样合并后就不是一个左式堆了），所以我们还得把它的左子树跟右子树对换，然后把它的零路径长设为右子树的零路径长加1；

LeftQueue* Merge(LeftQueue* nH1,LeftQueue* nH2)
{

if(nH1==NULL) return nH2;
if(nH2==NULL) return nH1;
LeftQueue* retqueue;
if(nH1->element<nH2->element)
{
retqueue=Merge1(nH1,nH2);
}
else
{
retqueue=Merge1(nH2,nH1);
}

return retqueue;
}

LeftQueue* Merge1(LeftQueue* nH1,LeftQueue* nH2)
{

if(nH1->rightNode==NULL)
{
nH1->rightNode=nH2;
}
else
{
nH1->rightNode=Merge(nH1->rightNode,nH2);
if(nH1->rightNode->nullPathLength>nH1->leftNode->nullPathLength)
{
SwapChildren(nH1);
}
nH1->nullPathLength=nH1->rightNode->nullPathLength+1;
}

return nH1;
}

LeftQueue* Insert(LeftQueue* nqueue,ElementData nelement)
{
LeftQueue* tmpqueue;
tmpqueue=new LeftQueue();
tmpqueue->element=nelement;
tmpqueue->nullPathLength=0;
tmpqueue->leftNode=tmpqueue->rightNode=NULL;
return Merge(nqueue,tmpqueue);
}

LeftQueue* DeleteMin(LeftQueue* nqueue)
{
LeftQueue* leftstack;
LeftQueue* rightstack;
leftstack=nqueue->leftNode;
rightstack=nqueue->rightNode;
free(nqueue);
return Merge(leftstack,rightstack);
}

11、散列表

概念：
理想的散列表是一个包含关键字的固定大小的数组，而散列函数就是计算每个关键字映射到数组中的对应位置(同时不同的两个关键字不可对应到同一个位置）.

一个简单的计算关键字为字符串时的散列函数：

unsigned int Hash(const char* key,int tablesize)
{
unsigned int reval=0;
while(*key!='/0')
{
reval+=*key++;
}
return reval%tablesize;
}

散列表过大时的一个散列函数：
这个只考察前3个字符,有27*27*27种组合

unsigned int Hash(const char* key, int tablesize)
{
return (key[0]+key[1]*27+key[2]*27^2)%tablesize;
}

下面是一个可以考察所有字符的散列函数

上面散列函数据用公式：k0+k1*n+k2*n*n;可转换为：(k2*n+k1)*n+k0

unsigned int Hash(const char* key,int tablesize)
{
unsigned int hashval=0;
while(*key!='/0')
{
hashval=hashval<<5+*key++;
}
return hashval%tablesize;
}

分离链接法（separate chaining）:其做法是将散列到同一个位置的元素以一个链表的方式保存。通常产生冲突的元素被插入到链表的最前面，这样不仅方便，而且由于最后插入的元素最有可能不久再使用，这样在查找起来效率会增加。分离链接实现简单，但是双向链表会占用额外的内存，冲突严重时，查找效率也会严重下降;
以下是个分离链接散列表，它可以用来解决冲突

struct ListNode
{
数据；
ListNode* lpNext;
};

typedef ListNode *HashElement;

struct HashTable
{
int tablesize;
HashElement* thelist;
}

HashTable* InitHash(int tablesize)//初始化散列表
{
HashTable* lphashtb;
lphashtb=new HashTable();
lphashtb->tablesize=tablesize;
lphashtb->thelist=new HashElement[tablesize];
for(int i=0;i<tablesize;i++)
{
lphashtb->thelist[i]=new ListNode();
lphashtb->thelist[i]->lpNext=NULL;
}

return lphashtb;
}

ListNode* Find(数据, HashTable h)//在分离链接散列表中查找数据
{
ListNode* tmpnode;
tmpnode=h->thelist[Hash(数据,h->tablesize)];

while(tmpnode!=NULL&&tmpnode->数据!=数据)
tmpnode=tmpnode->lpNext;

return tmpnode;
}

void Insert(数据,HashTable h)//插入数据到分离链接散列表中
{
ListNode* tmpnode;
tmpnode=Find(数据,h);
if(tmpnode==NULL)
{
ListNode* hashnode=h->thelist[Hash(数据,h)];
tmpnode=new ListNode();
tmpnode->lpNext=hashnode->lpNext;
tmpnode->数据=数据;
hashnode->lpNext=tmpnode;
}
}

开放地址散列表：
用开放定址法解决冲突的做法是：当冲突发生时，使用某种探查 ( 亦称探测 ) 技术在散列表中形成一个探查 ( 测 )序列。沿此序列逐个单元地查找，直到找到给定的关键字，或者碰到一个开放的地址 ( 即该地址单元为空 )为止（若要插入，在探查到开放的地址，则可将待插入的新结点存人该地址单元）。查找时探查到开放的地址则表明表中无待查的关键字，即查找失败。
注意：
① 用开放定址法建立散列表时，建表前须将表中所有单元 ( 更严格地说，是指单元中存储的关键字 ) 置空。

enum state
{
empty,
active
};

struct HashElement
{
数据;
state elementstate;
}

struct HashTable
{
int tablesize;
HashElement* thelist;
};

HashTable* InitHashTable(int tablesize)
{
HashTable* hashtable;
hashtable=new HashTable();
hashtable->tablesize=tablesize;
hashtable->thelist=new HashElement[tablesize];
for(int i=0;i<tablesize;i++)
{
hashtable->thelist[i]->elementstate=empty;
}
}

unsigned int Find(数据,HashTable* nHT)
{
unsigned int pos;
int collision_num=0;//冲突次数;
pos=Hash(数据,nHT->tablesize);
while(nHT->thelist[pos]->elementstate!=empty&&nHT->thelist[pos]->数据!=数据)
{
pos+=2*(++collision_num)-1;//增量为奇数;
if(pos>=nHT->tablesize)
{
pos-=nHT->tablesize;
}
}

return pos;
}

void Insert(数据,HashTable nHT)
{
unsigned int pos;

pos=Find(数据,nHT);

if(nHT->thelist[pos]->elementstate==empty)
{
nHT->thelist[pos]->elementstate=active;

nHT->thelist[pos]->数据=数据;
}

}

12、排序

插入排序：插入算法（insertion sort）把要排序的数组分成两部分：第一部分包含了这个数组的所有元素，但将最后一个元素除外，而第二部分就只包含这一个元素。在第一部分排序后，再把这个最后元素插入到此刻已是有序的第一部分里的正确位置中。

void InsertSort(Element ele[],int size)
{

for(int i=1;i<size;i++)
{
Element data=ele[i];
int index;
for(index=i;index>0&&ele[index-1]>ele[index];index--)
{
ele[index]=ele[index-1];
}

ele[index]=data;

}

}

希尔排序:
希尔排序算法是对插入排序的一种改进，其核心是减少已排序区域的右移次数来提高速度。具体做法是先获得一个间隔数值 h，然后将 n-1 替换成 n-h 来完成插入排序。其中不同的间隔数值的选取会影响到整个排序的效率;
将插入排序稍改下就成了希尔排序

void InsertSort(Element ele[],int size)
{
int increment;//新增加一个间隔量

for(increment=size/2;increment>0;increment/=2)//这也是新增的
{
for(int i=increment;i<size;i++)
{
Element data=ele[i];
int index;
for(index=i;index>=increment&&ele[index-increment]>ele[index];index-=increment)
{
ele[index]=ele[index-increment];
}

ele[index]=data;

}

}
}

13、图论

如果图中的边都是有方向的则为：有向图；

如果图中的边都是无方向的则为：无向图；

图的两种表示方法：
1、使用二维数组（又称邻接矩阵）：这样种的数组大小需要顶点数^2;
2、使用邻接表：在图是稀疏时候最好用这个；结构如下图表示；也就是对每个顶点,我们使用链表来存放所有它的邻接顶点；其中最左边只是个表头。用数组来表示表头.

最短路径算法：

赋权路径值：指路径上权值的总和；
无权路径值：指路径上的边数；

以下是一个应用广度优先搜索算法的计算无权路径的伪代码；
void UnWeight(Table T)
{
for(int curdist=0;curdist<VertexNum;curdist++)
{
for each vertex v
{
if(!T[v].know&&T[v].dist==curdist)
{
T[v].know==true;
for w to 其邻接顶点
{
if(T[w].dist==UnDist)
{
T[w].FatherVertex=v;
T[w].dist=curdist++;
}
}
}
}
}
}

使用队列精练后的计算无权路径的伪代码：

void UnWeight(Table T)
{
Queue q;
Vertex tmpvt;
q=CreateQueue(NumVertex);
MakeEmpty(q);
Enqueue(StartVertex,q); //向队列中插入开始点
T[StartVertex].dist=0;
while(!IsEmpty(q))
{
tmpvt=Dequeue(q);
T[tmpvt].know=true;
for w to 其邻接顶点
{
if(T[w].dist==UnDist)
{
T[w].FatherVertex=v;
T[w].dist=T[tmpvt].dist+1;
Enqueue(w,q);
}
}
}
}

当权值不为负时计算赋权最短路径算法:
以下的CVW=顶点V到顶点W的值,UnDist=无穷大;

void Dijkstra(Table T)
{
Vertex v;
while(true)
{
v=找出know为false的Dist最小权值;
if(v==NULL) break;
T[v].know=true;
for w to v //循环此顶点的邻接点
{
if(!T[w].know)
{
if((T[v].Dist+CVW)<T[w].Dist)
{
T[w].Dist=T[v].Dist+CVW;
T[w].FatherVertex=v;
}
}
}
}
}

当权值为负时，也就是有以下这种情况时用下面这种方法,但这种花费时间比上面多(因为它要遍历所有有关顶点，而上面的只要遍历最小值就可以了)；
s->u>s->v->u;也就是v->u为负的情况;

void WeightNegative(Table T)
{
Queue q;
Vertex tmpvt;
q=CreateQueue(NumVertex);
MakeEmpty(q);
Enqueue(StartVertex,q); //向队列中插入开始点
while(!IsEmpty(q))
{
tmpvt=Dequeue(q);
for w to v
{
if((T[tmpvt].Dist+CVW)<T[w].Dist)
{
T[w].Dist=T[tmpvt].Dist+CVW;
T[w].FatherVertex=tmpvt;
if(w不在队列q中)
{
Enqueue(w,q);
}
}
}
}
}

在连通情况下求最小生成树的Prim算法(同Dijkstra算法差不多，只是改Dist为V到W的距离(这样保证了各个顶点两两的距离为最优的)）:

void MinTree(Table T)
{
Vertex v;
while(true)
{
v=找出know为false的Dist最小权值;
if(v==NULL) break;

T[v].know=true;
for w to v
{
if(!T[w].know)
{
T[w].Dist=Min(CVW,T[w].Dist);
T[w].FatherVertex=v;
}
}
}
}

Kruskal算法计算最小生成树：

void Kruskal(Table T)
{
TreeSet ts;//森林,开始的时候每个顶点为一棵树
Queue H;//优先队列;
Edge E;//边=(顶点1，顶点2）
H=BuldHead(T);
int tmpnum=0;
while(tmpnum<VertexNum-1)
{
E=DeleteMin(H);//得到最小边
Tree ut=Find(E.Vertex1);
Tree vt=Find(E.Vertex2);
if(ut!=vt)
{
tmpnum++;
ConbinTree(ts,ut,vt);//合并树ut和vt
}
}
}

深度优先搜索算法：
下面是一个深度优先搜索的模版
void DFS(Vertex V)
{
Visited[V]=true;
for W to V //顶点V的临接顶点
{
if(!Visited[W])
{
DFS（W）；
}
}
}

14、树的遍历：

先序遍历：当前节点先于其儿子进行处理；
中序遍历：先遍历左子树，再遍历当前节点，最后在右子树；
后序遍历：先处理两个子树，最后再处理当前节点；
层序遍历：与其它遍历不同，其遍历方法使用的是一个队列外加一个循环而不是递归;

15、算法设计技巧：

(1)文件压缩算法：正常的ASCII编码等需要的比特数很大，所以人们想到是否提供一种可以降低比特数的编码；

哈夫曼编码：二进制代码可以用二叉树来表示，树只在树叶上有数据，每个字符从要节点开始以左分支为0，右分支为1,以记录路径的方式表示出来。最初先把每个字符作为树，然后依照频率，选取最小的两个进行合并,接着从这个合并树同其它树中找出最小频率，然后再合并，依其类推；

(2)随机数发生器：Seedn+1=(A*Seedn)Mod M
其中当M为素数时，总存在一个A可以使Xn的值周期为M-1(也就是满周期);上面那个算式当A太大时会溢出，所以我们使用以下这个：Seedn+1=A*(Seedn%Q)-R*(Seedn/Q)其中Q为M/A的商，R为M/A的余。