
📃博客主页: 小镇敲码人
💚代码仓库,欢迎访问
🚀 欢迎关注:👍点赞 👂🏽留言 😍收藏
🌏 任尔江湖满血骨,我自踏雪寻梅香。 万千浮云遮碧月,独傲天下百坚强。 男儿应有龙腾志,盖世一意转洪荒。 莫使此生无痕度,终归人间一捧黄。🍎🍎🍎
❤️ 什么?你问我答案,少年你看,下一个十年又来了 💞 💞 💞

🌍 最短路问题
🌕 单源最短路算法
🌰 Dijkstra算法
解决一个顶点到多个顶点的的最短路问题(单源),通常是在有权图中,但是不能处理负数权的情况。
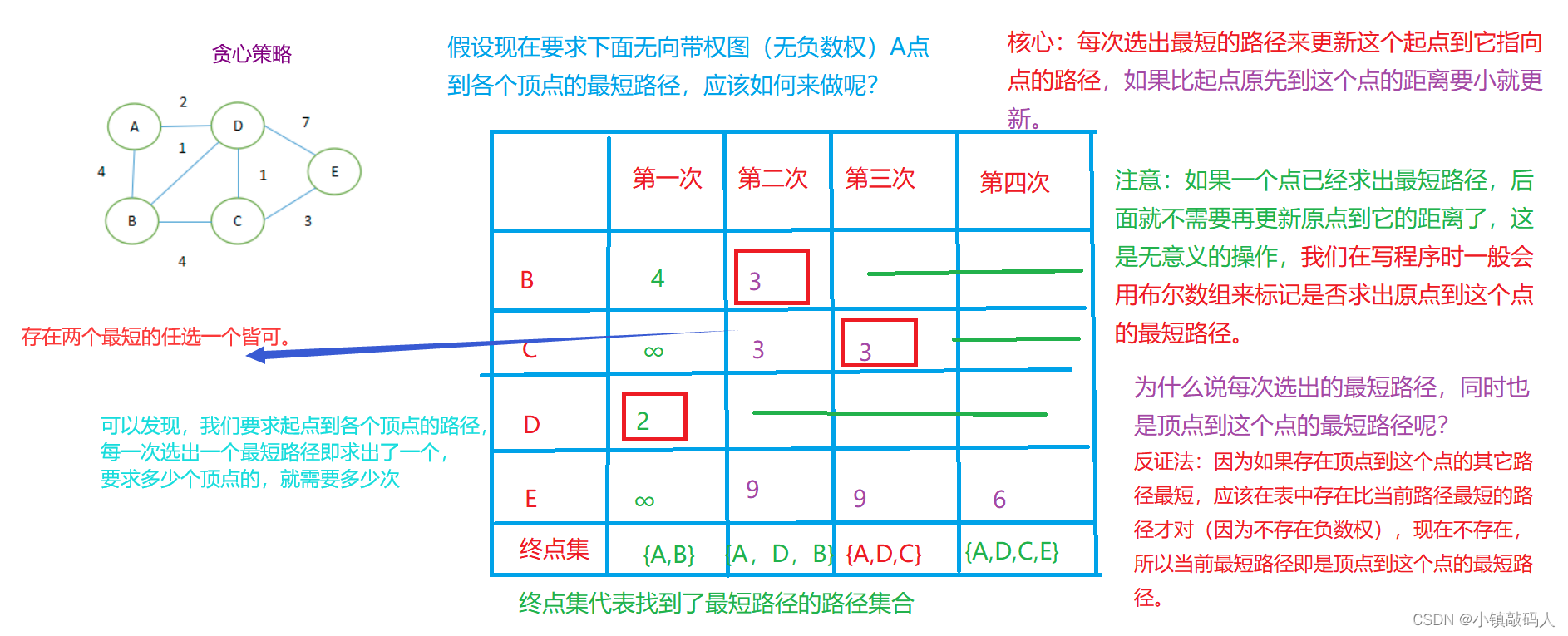
🎇 算法原理图解
算法核心:每一次找出距离起点最短的长度那个点,把它标记为找到了最短路径,然后用这个点更新其它点。
🎇 代码实现
🎑 朴素版本
//我们这里处理的是无向图,如果是有向图微调即可
long long Dijkstra1(int n, vector<vector<int>> road, int start, int end)//最短路算法,Dijkstra算法实现,返回顶点x到其它顶点的距离,road数组保存着每条边的开始的点,和结束的点以及它的权值
{
//首先我们需要初始化邻接表,因为road并不是,road只是每条边的信息
vector<vector<pair<int,int>>> G(n);//假设节点从0开始
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//无向图
G[node1].push_back({ node2,w });
G[node2].push_back({ node1,w });
}
vector<long long> dist(n, LLONG_MAX / 2);//dist数组存放起点start到每个节点之间的距离,一开始全部初始化为最大值的一半,为什么是一半呢?这里是防止溢出
dist[start] = 0;//start自己到自己的距离是0
vector<bool> find(n, false);//find数组是标记是否找到了节点start到i的最短路径
vector<int> pre(n);//保存每个节点最短路径的上一个节点
pre[start] = -1;//起点没有上一个节点
int min_i = -1;
while (1)
{
min_i = -1;
for (int i = 0; i < n; ++i)
{
if (!find[i] && (min_i == -1 || dist[min_i] > dist[i]))
{
min_i = i;
}
}
if (min_i == -1)
break;
find[min_i] = true;//说明这个点已经找到了起点到它的最短路径,标记为true
//用这个最短路径的点去更新其它的点
for (auto& node:G[min_i])
{
long long newdis = node.second + dist[min_i];
if (newdis < dist[node.first])//如果比我现在的距离要小,就更新距离和上一个节点的下标
{
dist[node.first] = newdis;
pre[node.first] = min_i;
}
}
}
return dist[end];
}
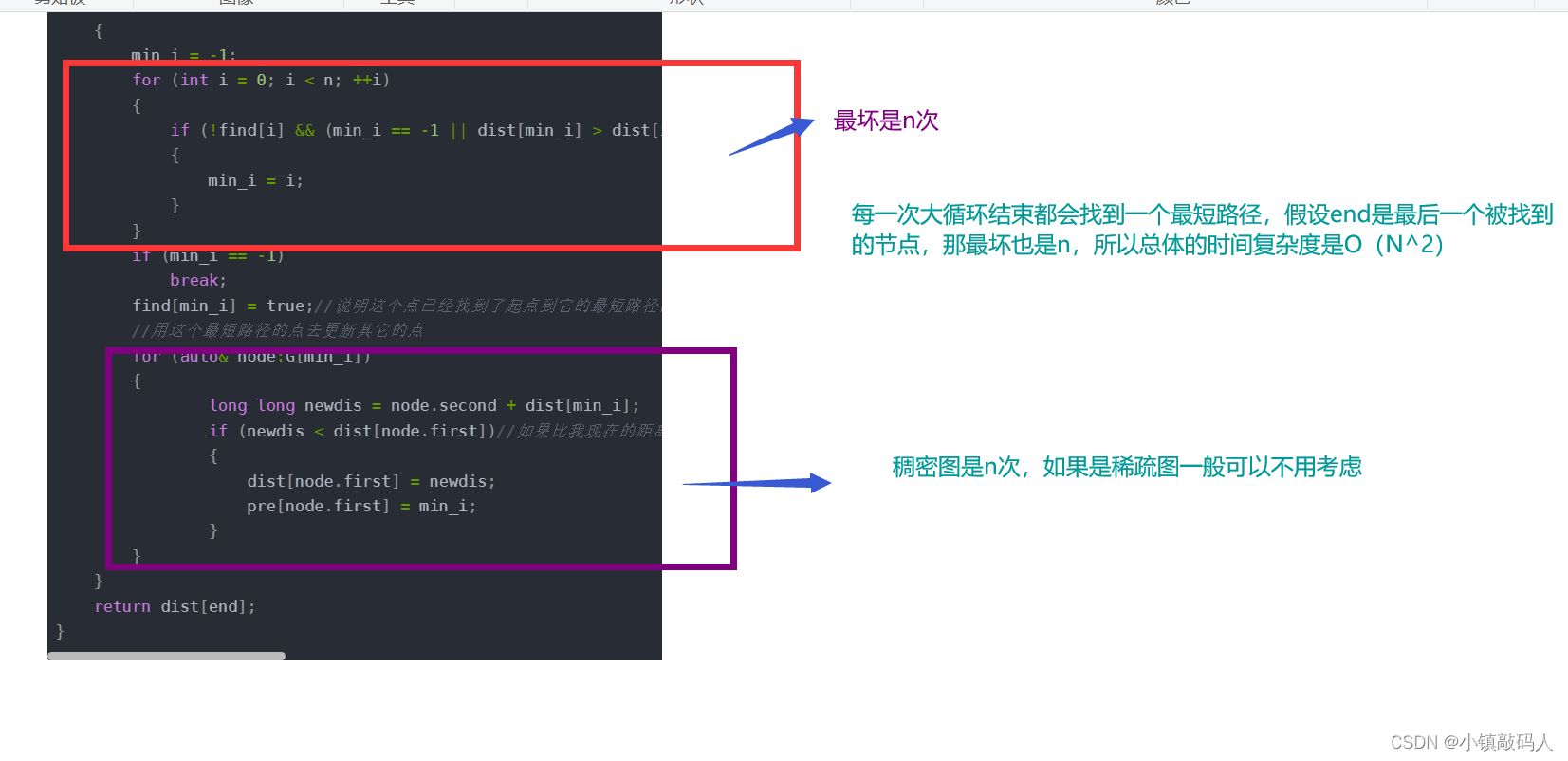
📪 朴素版本的时间复杂度分析
时间复杂度为 O ( N 2 ) O(N^2) O(N2)。
🎑 优先队列(堆)优化版本
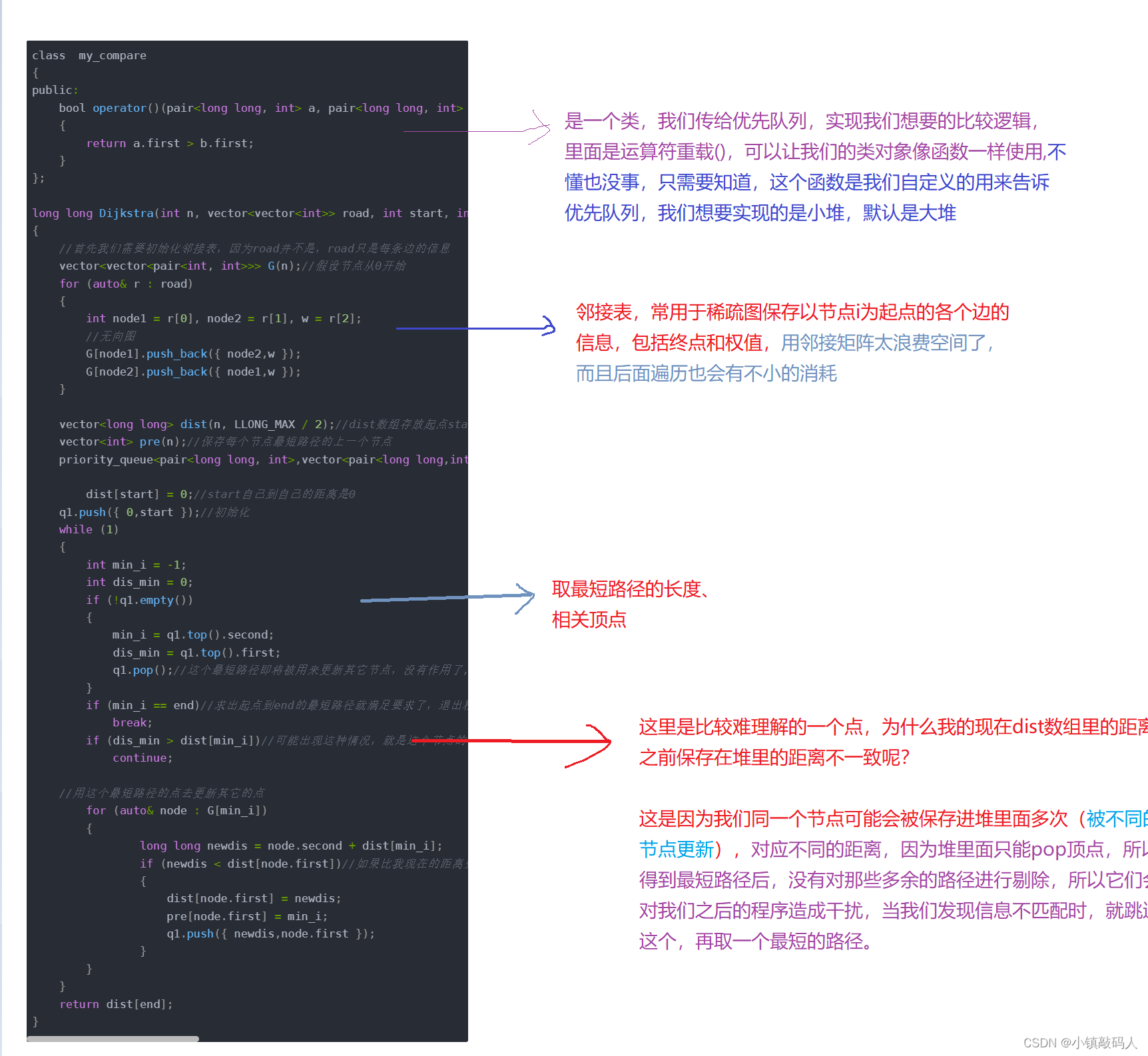
原理阐述:
使用优先队列(小堆),每一次存入{路径、节点},可以让我们在logN的量级下就找到最短路径,及其对应的节点,反观第一种朴素版本,找最短路径则要老老实实的遍历。每一次更新节点的路径之后都要存入优先队列中。其它的地方和第一种版本基本一致。
这里对代码比较难理解的地方做一下说明:
class my_compare
{
public:
bool operator()(pair<long long, int> a, pair<long long, int> b)
{
return a.first > b.first;
}
};
long long Dijkstra2(int n, vector<vector<int>> road, int start, int end)//最短路算法,Dijkstra算法实现,优先队列优化版本
{
//首先我们需要初始化邻接表,因为road并不是,road只是每条边的信息
vector<vector<pair<int, int>>> G(n);//假设节点从0开始
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//无向图
G[node1].push_back({ node2,w });
G[node2].push_back({ node1,w });
}
vector<long long> dist(n, LLONG_MAX / 2);//dist数组存放起点start到每个节点之间的距离,一开始全部初始化为最大值的一半,为什么是一半呢?这里是防止溢出
vector<int> pre(n);//保存每个节点最短路径的上一个节点
priority_queue<pair<long long, int>,vector<pair<long long,int>>,my_compare> q1;//创建一个小根堆,来更快的求出每次的最短路径
dist[start] = 0;//start自己到自己的距离是0
pre[start] = -1;//起点没有上一个节点
q1.push({ 0,start });//初始化
while (1)
{
int min_i = -1;
int dis_min = 0;
if (!q1.empty())
{
min_i = q1.top().second;
dis_min = q1.top().first;
q1.pop();//这个最短路径即将被用来更新其它节点,没有作用了,从优先队列中pop掉
}
if (min_i == end)//求出起点到end的最短路径就满足要求了,退出程序
break;
if (dis_min > dist[min_i])//可能出现这种情况,就是这个节点的信息之前就已经存入队列中了,但是再次更新之后没有把旧的信息删除,就会造成这种不匹配的现象,我们跳过这种不合法的情况
continue;
//用这个最短路径的点去更新其它的点
for (auto& node : G[min_i])
{
long long newdis = node.second + dist[min_i];
if (newdis < dist[node.first])//如果比我现在的距离要小,就更新距离和上一个节点的下标
{
dist[node.first] = newdis;
pre[node.first] = min_i;
q1.push({ newdis,node.first });
}
}
}
return dist[end];
}
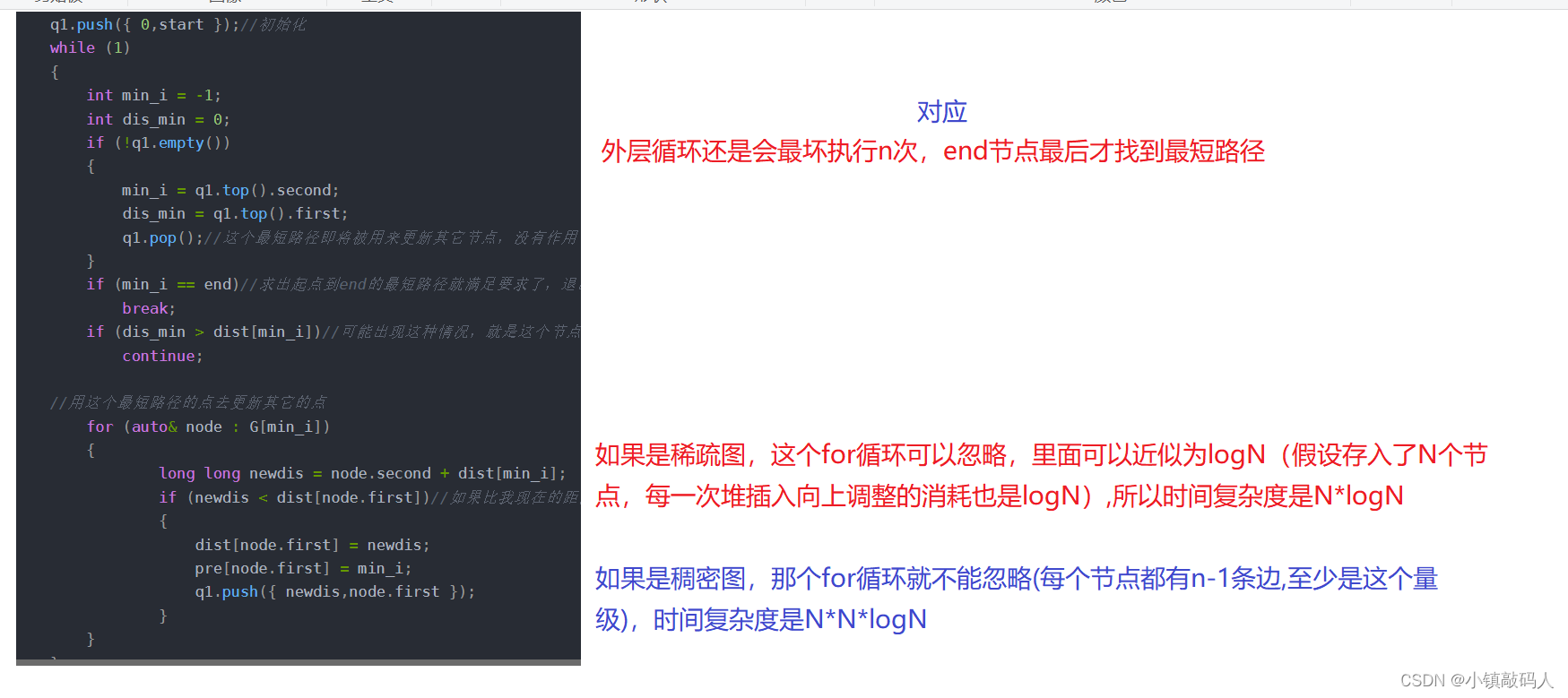
📪 优先队列版本的时间复杂度分析
对于稀疏图而言,它的时间复杂度是 O ( N ∗ l o g N ) O(N*logN) O(N∗logN),对于稠密图而言,它的时间复杂度是 O ( N 2 ∗ l o g N ) O(N^2*logN) O(N2∗logN),反而不如第一种优秀。
🎑 样例测试,求最短路径长度并打印最短路径
这里我们用下图的数据来进行测试:
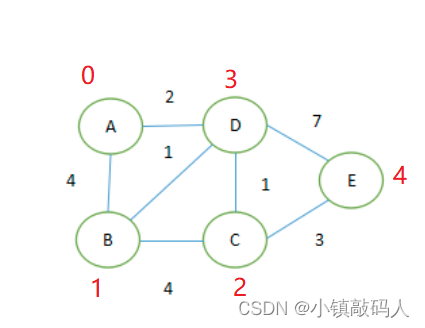
测试程序:
void Test_Dijkstra()
{
int n = 0;
cout << "请输入节点个数:" << endl;
cin >> n;
int start = 0, end = 0;
cout << "请输入要求的最短路径的起点和终点:" << endl;
cin >> start >> end;
vector<vector<int>> road;
cout << "请输入对应的边的起点、终点、及其权值:" << endl;
int s, e, w = 0;
while (cin >> s >> e >> w)
{
road.push_back({ s,e,w });
}
printf("Dijkstra1: ");
Dijkstra1(n, road, start, end);//打印最短路径长度和路径
printf("Dijkstra1: ");
Dijkstra2(n, road, start, end);//打印最短路径长度和路径
}
打印最短路径的函数:
void PrintLength(vector<int> pre, int cur)//打印最短路径
{
if (cur == -1)
{
return;
}
PrintLength(pre, pre[cur]);//先去递归前驱节点,再回来打印
if (pre[cur] == -1)
printf("%d", cur);
else
printf("->%d", cur);
}
稍作修改的Dijkstra算法函数:
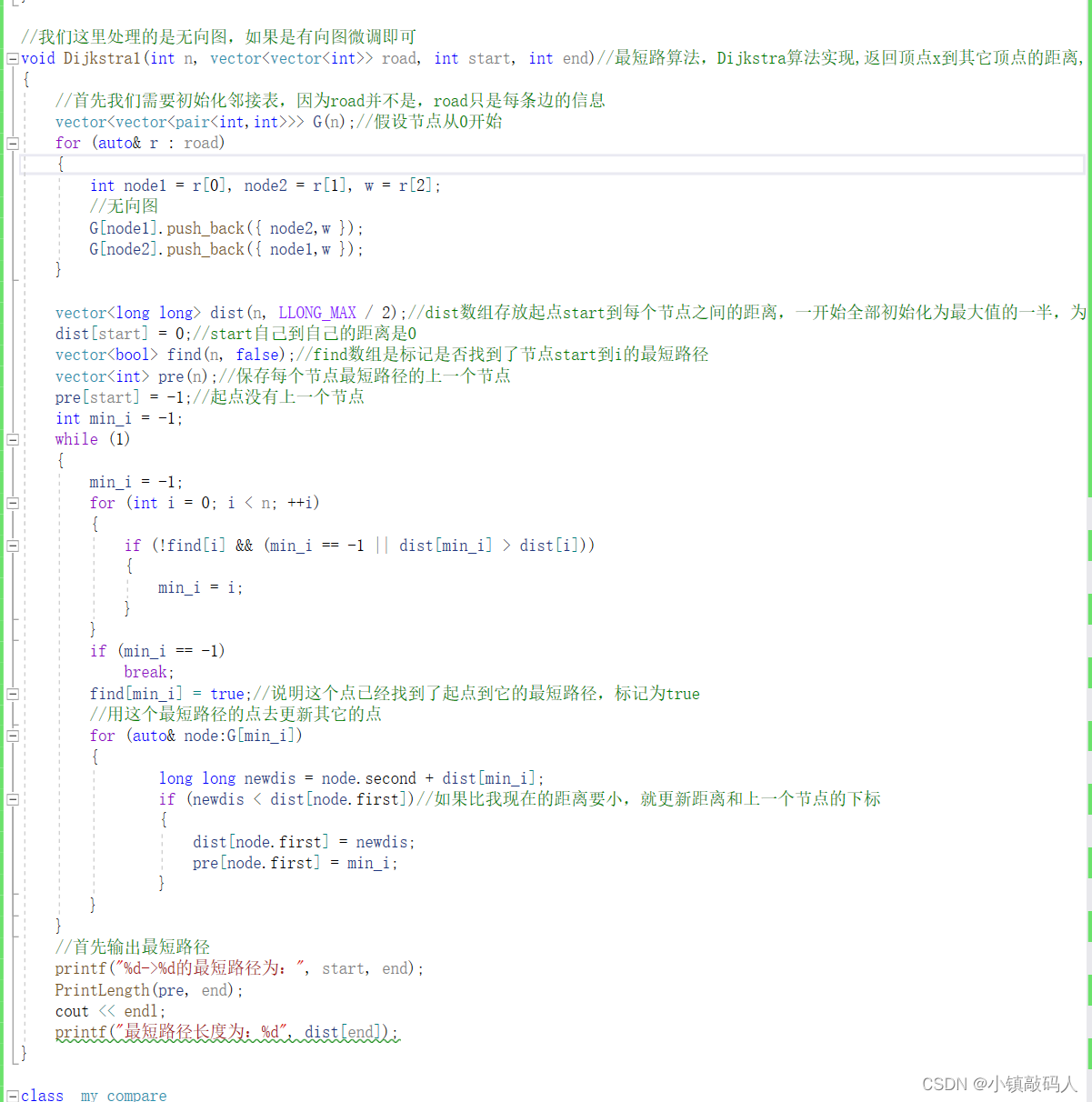
运行结果与我们之前手算的比较:
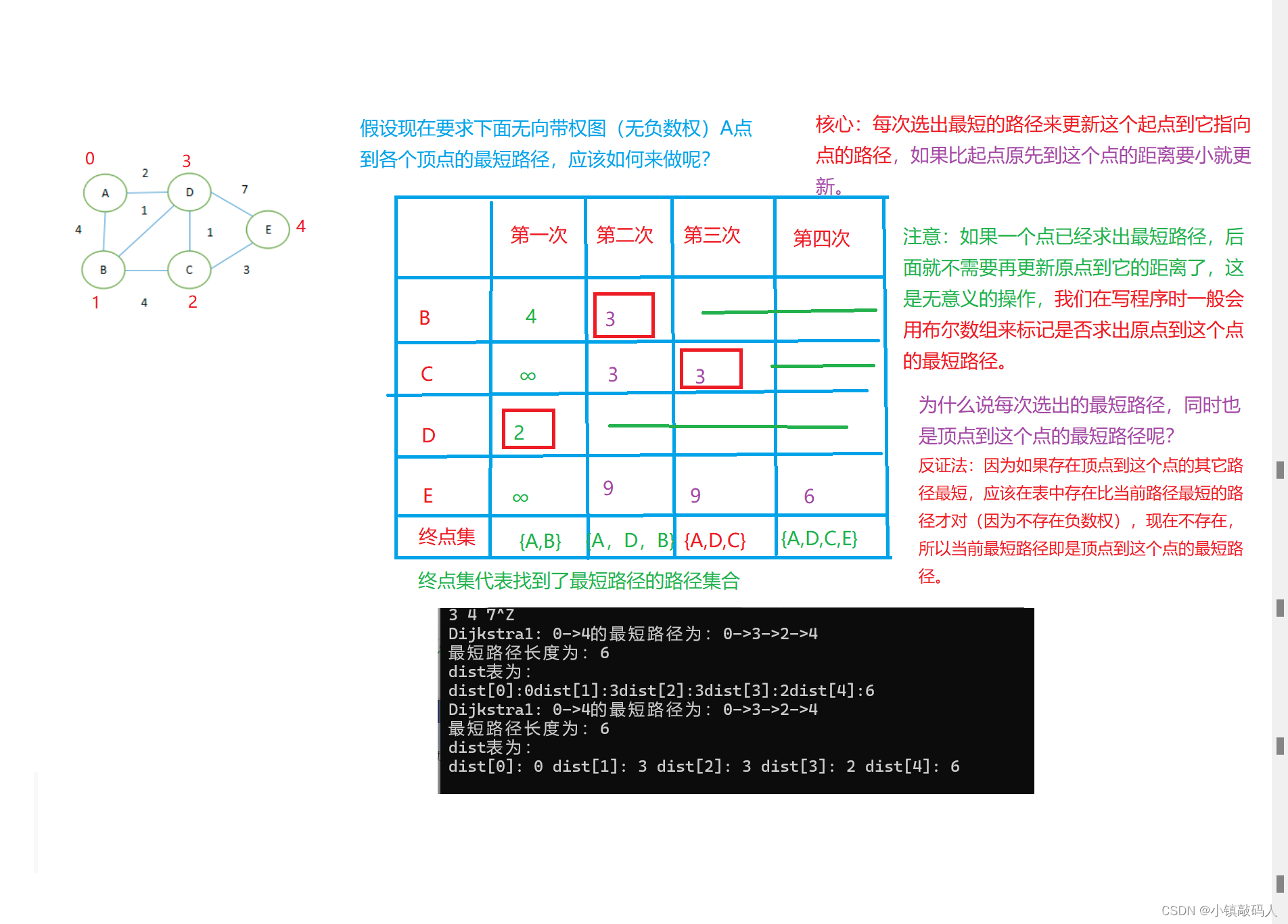
结果一致。
🌰 Bellman-ford算法–处理负权问题
🎇 算法原理讲解
核心思路:看是否可以加入G[i][j]这条边,使得start顶点到顶点j的距离变短。

🎇 代码实现
void Bellman_ford(int n, vector<vector<int>> road, int start, int end)//单源算法可处理负权,假设是无向图
{
//我们还是使用邻接表保存每条边的信息,因为有时候是无向图,不会把双向的边都表示出来
vector<vector<pair<int,int>>> G(n);
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//无向图
G[node1].push_back({ node2,w });
G[node2].push_back({ node1,w });
}
vector<long long> dis(n,LLONG_MAX/2);//dis[i]表示顶点start到i的距离
vector<int> pre(n);//pre[i]:表示start到i的最短路径,i的前驱节点
pre[start] = -1;//start没有前驱节点
dis[start] = 0;
for (int i = 0; i < n - 1; ++i)//n个节点,至多n-1次就可以求出最优路径
{
//枚举每条边
for (int j = 0; j < n; ++j)
{
for (auto& k : G[j])
{
int x = k.first, w = k.second;
if (dis[j] + w < dis[x])//如果加j->x这条边,可以让dis[x]的值变小,就更新
{
pre[x] = j;
dis[x] = dis[j]+w;
}
}
}
}
}
解释一下为什么至多n-1次就可以算出最短路径:
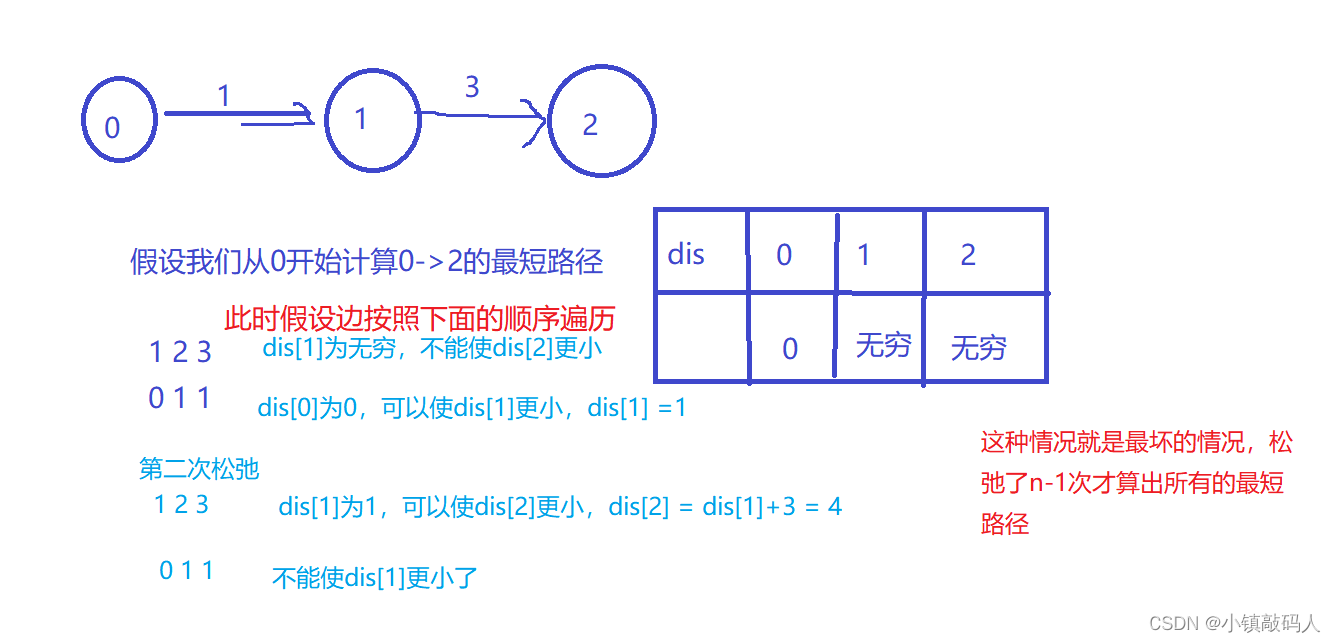
这个算法不能处理负环的问题,负环就是每经过一次这个环,距离就会减少,我们无法算出最短路径。可以遍历所有的边再判断,如果还能算出更短的路径,就可以说明存在负环,我们打印相关信息即可。
优化后的代码:
void Bellman_ford(int n, vector<vector<int>> road, int start, int end)//单源算法可处理负权,假设是无向图
{
//我们还是使用邻接表保存每条边的信息,因为有时候是无向图,不会把双向的边都表示出来
vector<vector<pair<int,int>>> G(n);
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//无向图
G[node1].push_back({ node2,w });
G[node2].push_back({ node1,w });
}
vector<long long> dis(n,LLONG_MAX/2);//dis[i]表示顶点start到i的距离
vector<int> pre(n);//pre[i]:表示start到i的最短路径,i的前驱节点
pre[start] = -1;//start没有前驱节点
dis[start] = 0;
for (int i = 0; i < n - 1; ++i)//n个节点,至多n-1次就可以求出最优路径
{
//枚举每条边
for (int j = 0; j < n; ++j)
{
for (auto& k : G[j])
{
int x = k.first, w = k.second;
if (dis[j] + w < dis[x])//如果加j->x这条边,可以让dis[x]的值变小,就更新
{
pre[x] = j;
dis[x] = dis[j]+w;
}
}
}
}
bool flag = false;
//处理负环的情况
for(int j = 0;j < n;++j)
for (auto& k : G[j])
{
int x = k.first, w = k.second;
if (dis[j] + w < dis[x])
{
flag = true;
break;
}
}
if (flag)
{
printf("存在负环,不存在最短路径\n");
}
}
🎇 时间复杂度分析
时间复杂度为 O ( n m ) O(nm) O(nm),n为节点个数,m为边数
🎇 样例测试
测试函数:
void Test_Bellman_ford()
{
int n = 0;
cout << "请输入节点个数:" << endl;
cin >> n;
int start = 0, end = 0;
cout << "请输入要求的最短路径的起点和终点:" << endl;
cin >> start >> end;
vector<vector<int>> road;
cout << "请输入对应的边的起点、终点、及其权值:" << endl;
int s, e, w = 0;
while (cin >> s >> e >> w)
{
road.push_back({ s,e,w });
}
printf("Bellman_ford: ");
Dijkstra1(n, road, start, end);//打印最短路径长度和路径
}
运行结果(测试数据和上面的一致):
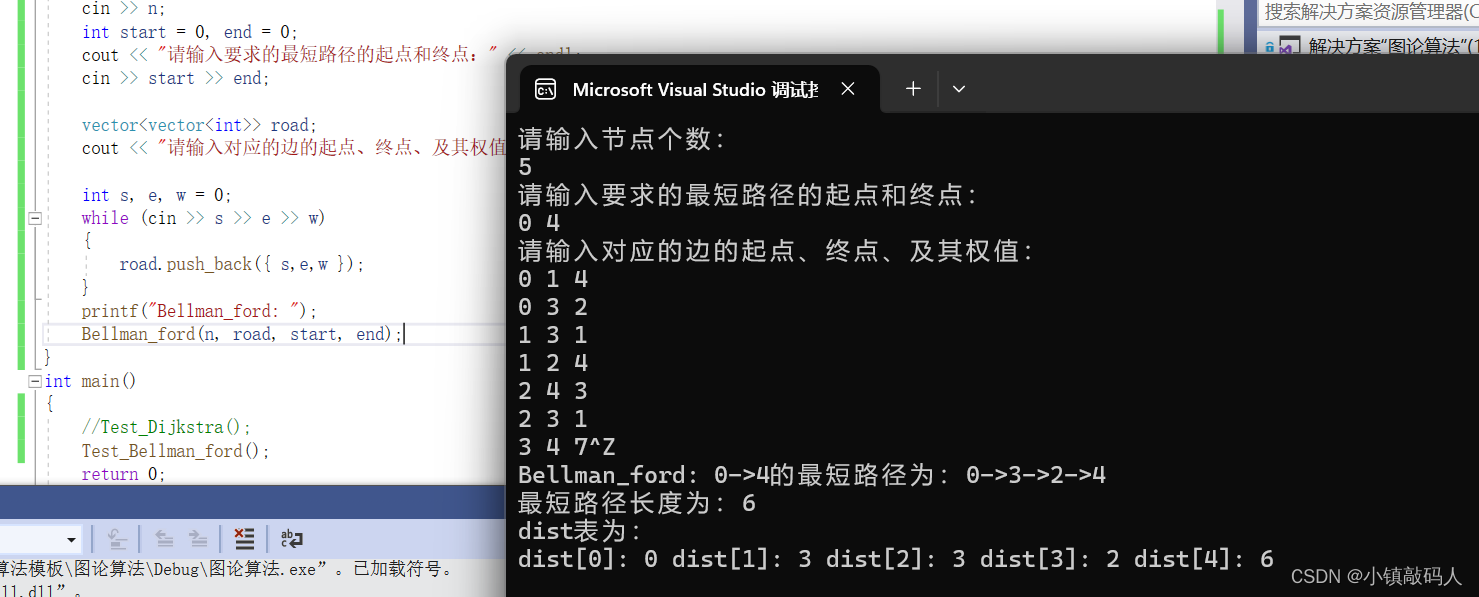
负权的数据运行结果:
数据:
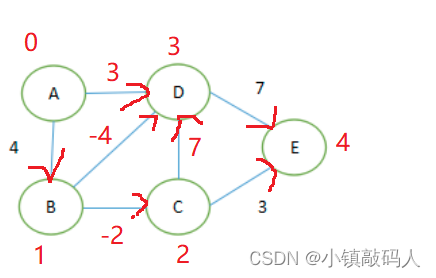
程序需要改成有向的否则双向负权就存在负环了。
运行结果:
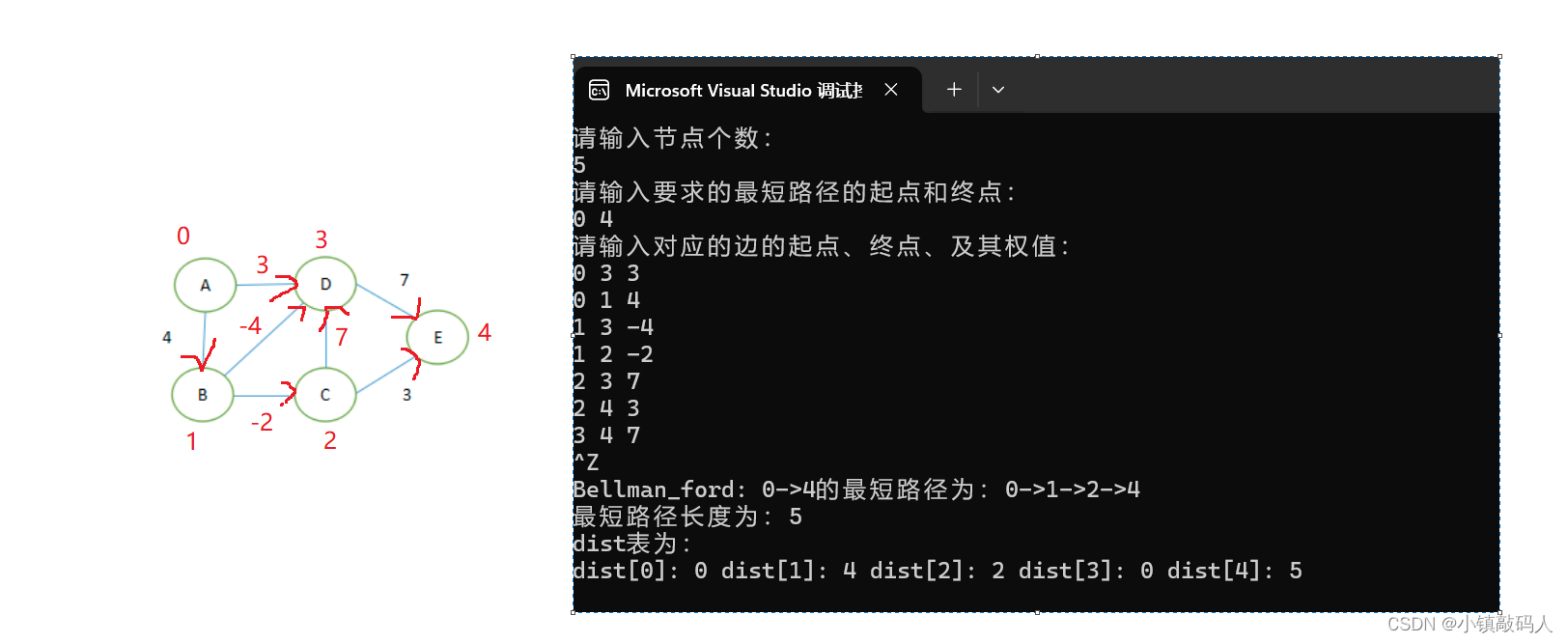
与预期一致。
1、2、3节点构成负环的情况:
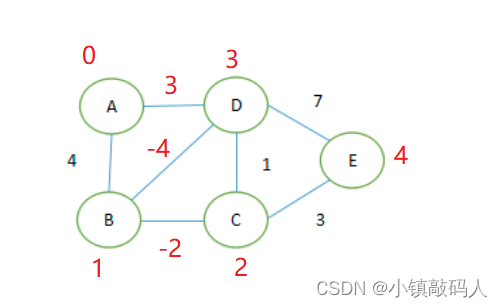
运行结果:
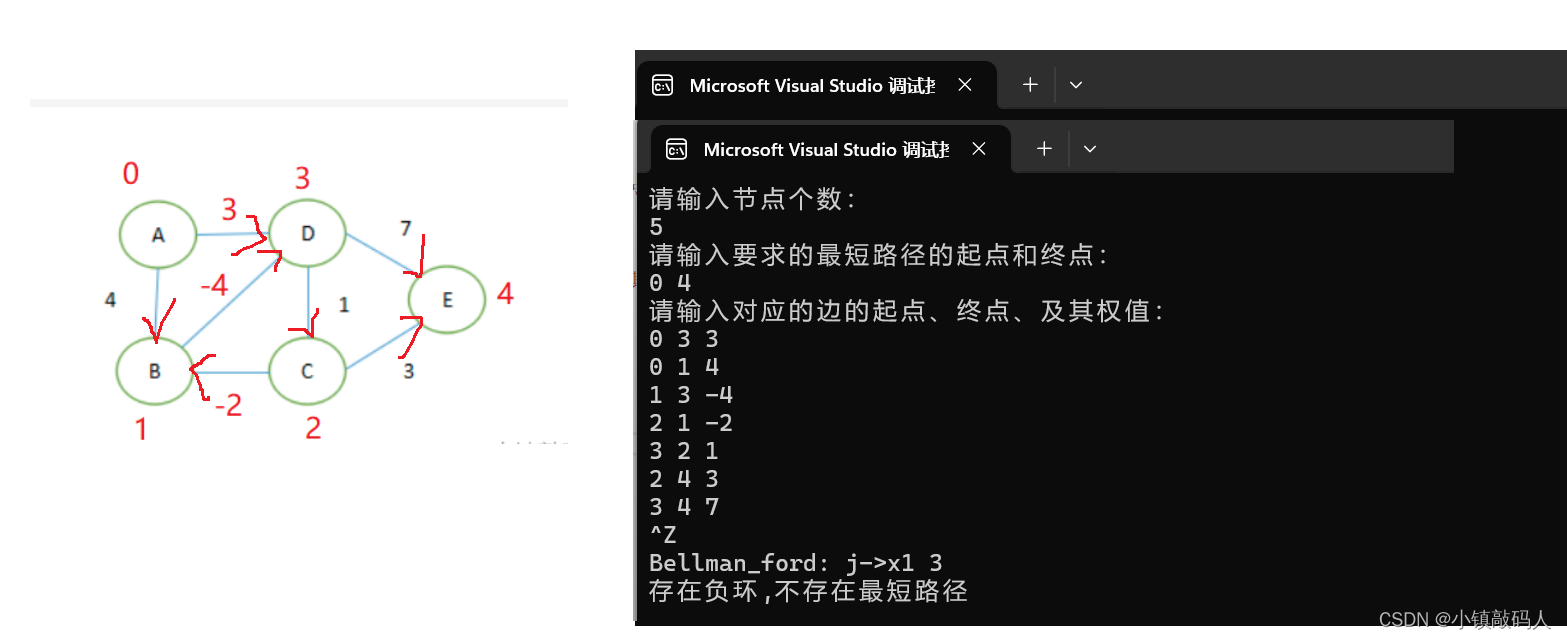
🌰 SPFA算法–Bellman-ford算法的优化
🎇 算法原理讲解
SPFA算法是Bellman算法的优化版本,因为Bellman算法外层循环是n-1,其实很多次都不用n-1次松弛就可以算出所有的最短路径。
核心思路:
使用一个队列来保存被更新最短路的节点,然后依次取队首节点,去用这个节点来更新它指向的邻居节点,还是通过边来松弛,直到队列为空,这里注意,当一个节点已经存在队列的时候,不能重复存储,但是可以被存多次,因为它的路径可能会被多次更新。
🎇 代码实现
🎑 普通版本
void SPFA1(int n, vector<vector<int>> road, int start, int end)//假设是有向图
{
//我们还是使用邻接表保存每条边的信息,因为有时候是无向图,不会把双向的边都表示出来
vector<vector<pair<int, int>>> G(n);
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//有向图
G[node1].push_back({ node2,w });
}
vector<long long> dis(n, LLONG_MAX / 2);//dis[i]表示顶点start到i的距离
vector<int> pre(n, -1);//pre[i]:表示start到i的最短路径,i的前驱节点
vector<bool> vis(n);//判断节点i是否在队列中,防止重复入队列
queue<int> q;
q.push(start);
vis[start] = true;
pre[start] = -1;//start没有前驱节点
dis[start] = 0;
//开始松弛
while (!q.empty())
{
int i = q.front();//取队首节点
q.pop();
vis[i] = false;
for (auto& node : G[i])//更新i指向的顶点
{
int j = node.first, w = node.second;//加入i->j这条边是否能使,dis[j]变短,如果能更新dis[j]
if (dis[i] + w < dis[j])
{
pre[j] = i;
dis[j] = dis[i] + w;
if(!vis[j])//如果j此时不在队列中
q.push(j);
vis[j] = true;
}
}
}
//首先输出最短路径
printf("%d->%d的最短路径为:", start, end);
PrintLength(pre, end);
cout << endl;
printf("最短路径长度为:%d\n", dis[end]);
printf("dist表为:\n");
for (int i = 0; i < dis.size(); ++i)
printf("dist[%d]: %d ", i, dis[i]);
cout << endl;
}
作为Bellman-ford算法的优化我们SPFA算法也可以判断图中是否出现负环,当然我们上面的代码没有体现(上面的代码如果出现负环就会死循环),下面我将用两种方式来写判断负环的版本:
🎑 判断负环版本1
如果不存在负环,我们正常最坏情况,一个节点松弛的次数是n-1次,如果松弛次数大于了这个值就证明存在负环,我们可以通过记录出队列或者入队列的次数来判断松弛的次数:
void SPFA2(int n, vector<vector<int>> road, int start, int end)//假设是有向图
{
//我们还是使用邻接表保存每条边的信息,因为有时候是无向图,不会把双向的边都表示出来
vector<vector<pair<int, int>>> G(n);
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//有向图
G[node1].push_back({ node2,w });
}
vector<long long> dis(n, LLONG_MAX / 2);//dis[i]表示顶点start到i的距离
vector<int> pre(n, -1);//pre[i]:表示start到i的最短路径,i的前驱节点
vector<bool> vis(n);//判断节点i是否在队列中,防止重复入队列
vector<int> slack(n);//记录每个节点松弛的次数
queue<int> q;
q.push(start);
vis[start] = true;
pre[start] = -1;//start没有前驱节点
dis[start] = 0;
bool flag = false;//记录是否存在负环
//开始松弛
while (!q.empty())
{
int i = q.front();//取队首节点
q.pop();
slack[i]++;//出队列,松弛次数++
vis[i] = false;
if (slack[i] > n - 1)
{
flag = true;
break;
}
for (auto& node : G[i])//更新i指向的顶点
{
int j = node.first, w = node.second;//加入i->j这条边是否能使,dis[j]变短,如果能更新dis[j]
if (dis[i] + w < dis[j])
{
pre[j] = i;
dis[j] = dis[i] + w;
if (!vis[j])//如果j此时不在队列中
q.push(j);
vis[j] = true;
}
}
}
if (flag)
{
printf("存在负环,无法求出最短路径\n");
}
else
{
//首先输出最短路径
printf("%d->%d的最短路径为:", start, end);
PrintLength(pre, end);
cout << endl;
printf("最短路径长度为:%d\n", dis[end]);
printf("dist表为:\n");
for (int i = 0; i < dis.size(); ++i)
printf("dist[%d]: %d ", i, dis[i]);
cout << endl;
}
}
🎑 判断负环版本2
上述方法可能不是最快的,我们也可以通过遍历每个节点的最短路径,如果这个路径的长度大于了n,就证明出现了负环。
bool PrintLength_Negative_loop(vector<int> pre, int cur, int n, int cur_cnt)//打印最短路径
{
if (cur == -1)
{
return false;
}
if (cur_cnt > n)//如果经过的顶点数量大于n,说明存在负环
{
return true;
}
bool flag = PrintLength_Negative_loop(pre, pre[cur], n, cur_cnt + 1);//先去递归前驱节点,再回来打印
if (pre[cur] == -1)
printf("%d", cur);
else
printf("->%d", cur);
return flag;
}
void SPFA3(int n, vector<vector<int>> road, int start, int end)//假设是无向图
{
//我们还是使用邻接表保存每条边的信息,因为有时候是无向图,不会把双向的边都表示出来
vector<vector<pair<int, int>>> G(n);
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//有向图
G[node1].push_back({ node2,w });
}
vector<long long> dis(n, LLONG_MAX / 2);//dis[i]表示顶点start到i的距离
vector<int> pre(n, -1);//pre[i]:表示start到i的最短路径,i的前驱节点
vector<bool> vis(n);//判断节点i是否在队列中,防止重复入队列
queue<int> q;
q.push(start);
vis[start] = true;
pre[start] = -1;//start没有前驱节点
dis[start] = 0;
//开始松弛
while (!q.empty())
{
int i = q.front();//取队首节点
q.pop();
vis[i] = false;
for (auto& node : G[i])//更新i指向的顶点
{
int j = node.first, w = node.second;//加入i->j这条边是否能使,dis[j]变短,如果能更新dis[j]
if (dis[i] + w < dis[j])
{
pre[j] = i;
dis[j] = dis[i] + w;
if (!vis[j])//如果j此时不在队列中
q.push(j);
vis[j] = true;
bool flag = PrintLength_Negative_loop(pre, j, n, 0);
if (flag)
{
printf("存在负环,无法求出最短路径\n");
}
}
}
}
}
🎇 时间复杂度分析
正常版本的SPFA算法的时间复杂度是 O ( c m ) O(cm) O(cm),c是常数,m是边数。
🎇 样例测试
测试函数和之前类似这里我们不再给出。
- 测试数据1(无负权,无向图):
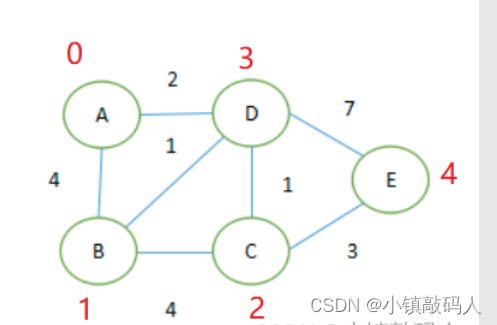
运行结果:

和预期一致。
- 测试数据2,有负权(但不成环),有向(这里代码邻接表部分要做一下微调)。
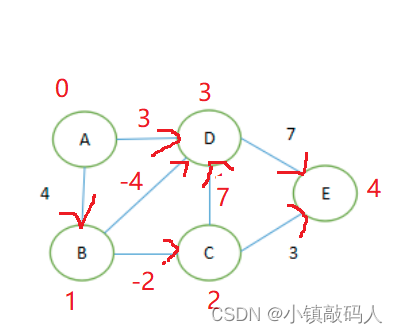
运行结果:
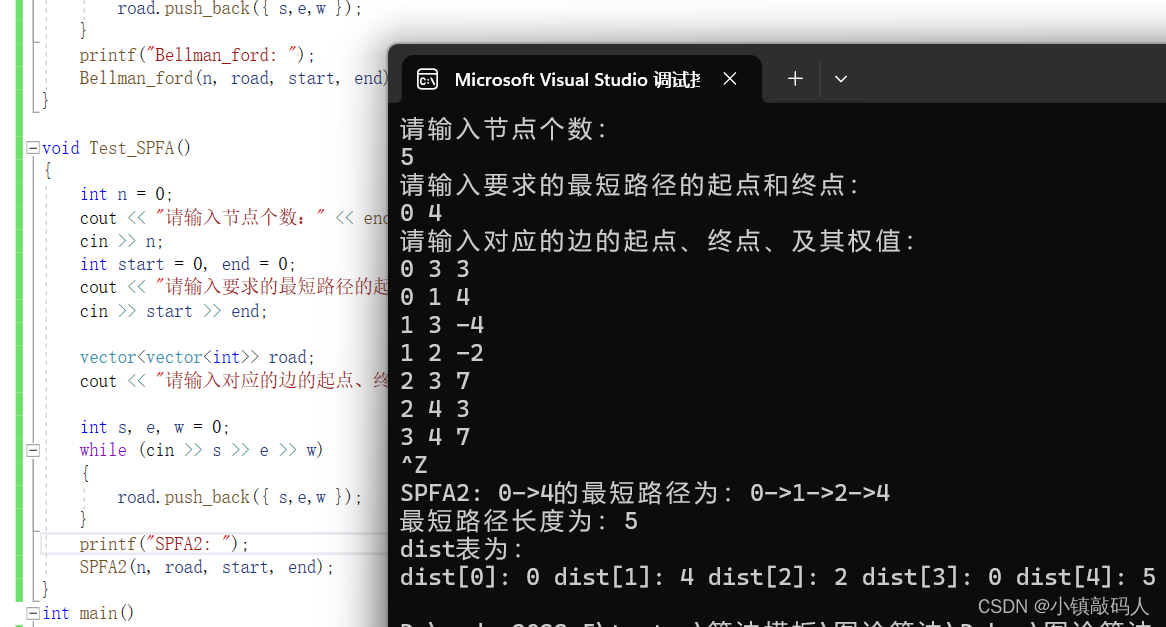
与预期一致。
- 测试数据31,2,3存在负环。
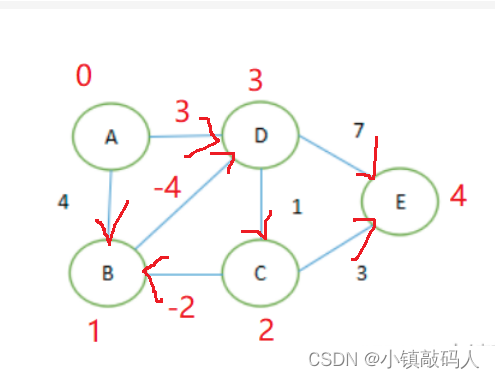
1、版本1测试,没有处理负环
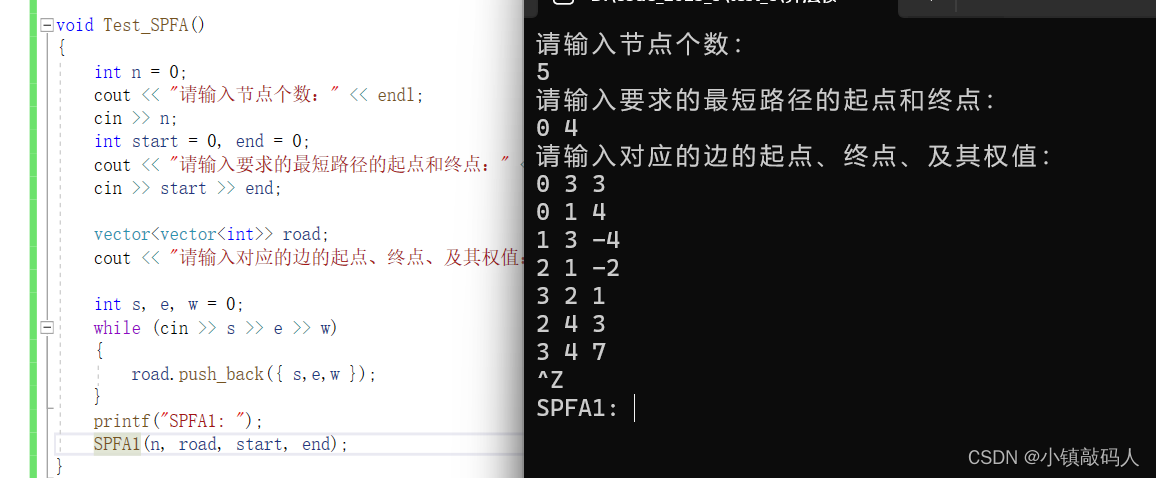
程序直接死循环了。
2、版本2测试
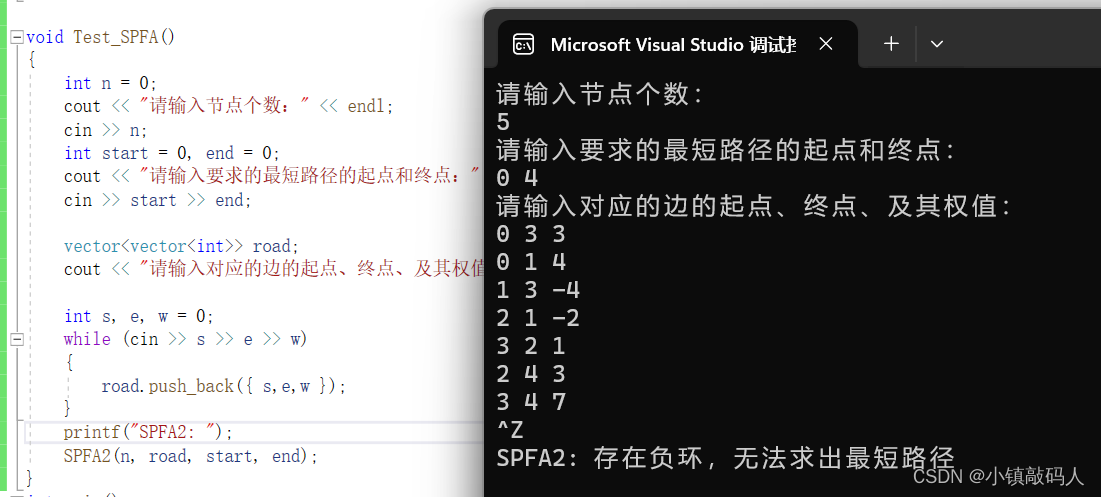
3、版本3 测试
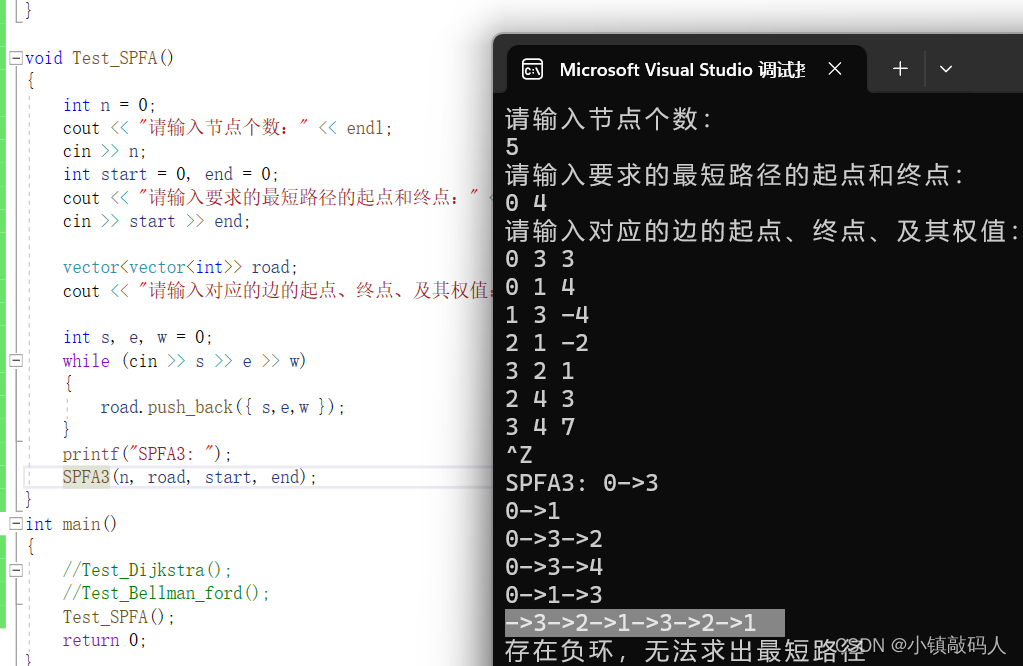
这里我们还可以看见负环是2,1,3。
🌕 多源最短路算法
上面几个算法都只能处理某一个顶点点到其它顶点的最短路径,但是不能求另外其它顶点到给节点的最短路径,下面我们来介绍一下多源最短路径算法–Floyed算法。
🌰 Floyed算法
🎇 算法原理图解
Floyed算法的核心在于:使用一个顶点作为过渡顶点,看是否加入可以让其它顶点的距离变小,等到把所有的节点遍历一次,就求出了所有节点间的最短路径。我们来画图分析一下:
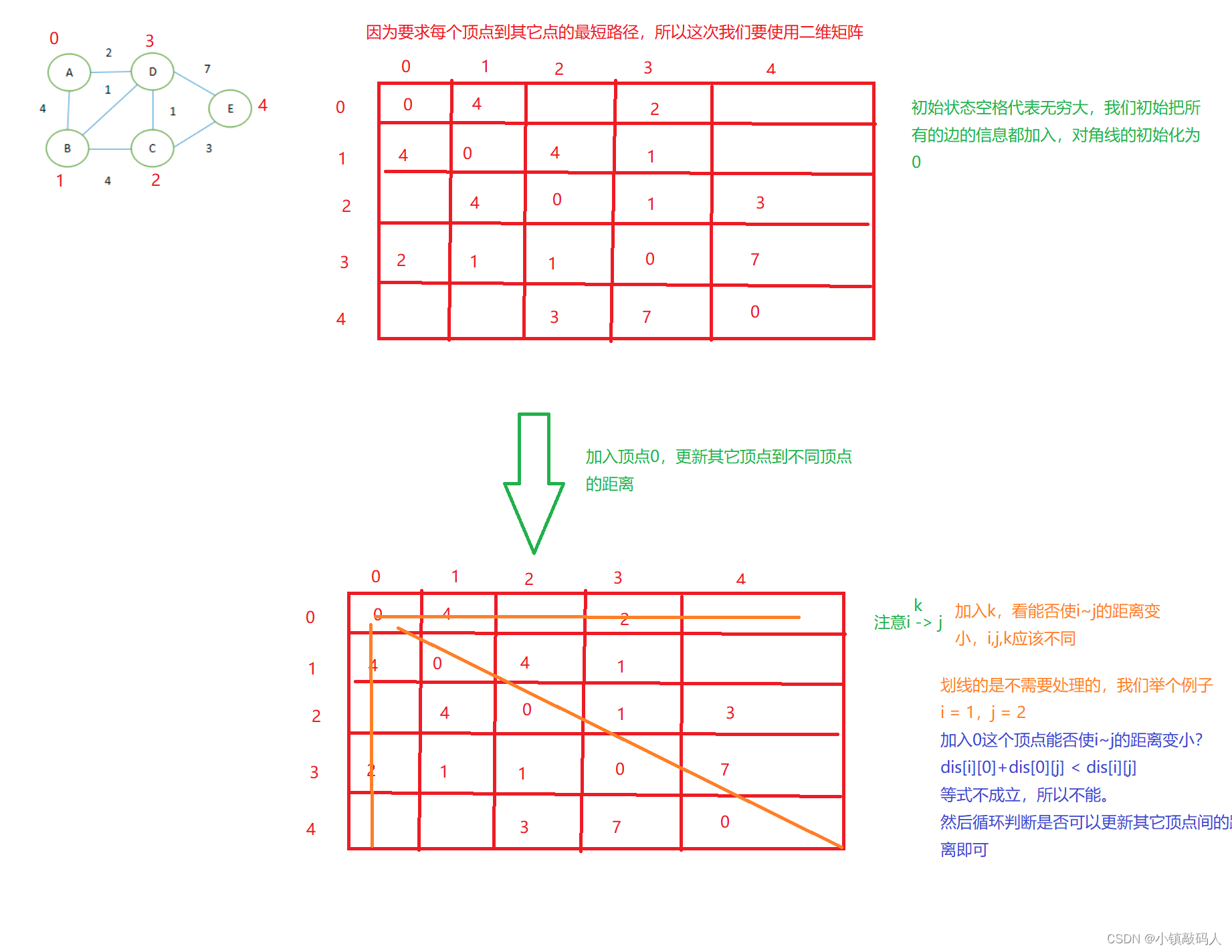
🎇 代码实现
void Floyed(int n,vector<vector<int>> road,int start,int end)//多源最短路算法可以处理负权,但是不能处理带有负环的图 N^3
{
vector<vector<long long>> dis(n, vector<long long>(n, LLONG_MAX / 2));//假设节点从0开始
vector<vector<int>> pre(n, vector<int>(n, -1));//保存边i~j的最短路径j前的前驱节点
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//无向图
dis[node1][node2] = w;
pre[node1][node2] = node1;
dis[node2][node1] = w;
pre[node2][node1] = node2;
}
//将对角线的距离都初始化为0
for (int i = 0, j = 0; i < n; ++i,++j)
{
dis[i][j] = 0;
}
//使用每个节点作为中间节点,去更新新其它的节点
for (int k = 0; k < n; ++k)
{
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
{
if (i == k)
break;
if (j == k || j == i)
continue;
if (dis[i][j] > dis[i][k] + dis[k][j])//用这个中间节点来更新
{
dis[i][j] = dis[i][k] + dis[k][j];
pre[i][j] = pre[k][j];
}
}
}
//首先输出最短路径
printf("%d->%d的最短路径为:", start, end);
PrintLength(pre[start], end);
cout << endl;
printf("顶点%d->顶点%d最短路径长度为:%d\n",start,end ,dis[start][end]);
printf("dist表为:\n");
for (int i = 0; i < dis[start].size(); ++i)
printf("dist[%d]: %d ", i, dis[start][i]);
cout << endl;
}
🎇 时间复杂度
标准的 O ( N 3 ) O(N^3) O(N3)的量级。
🎇 样例测试
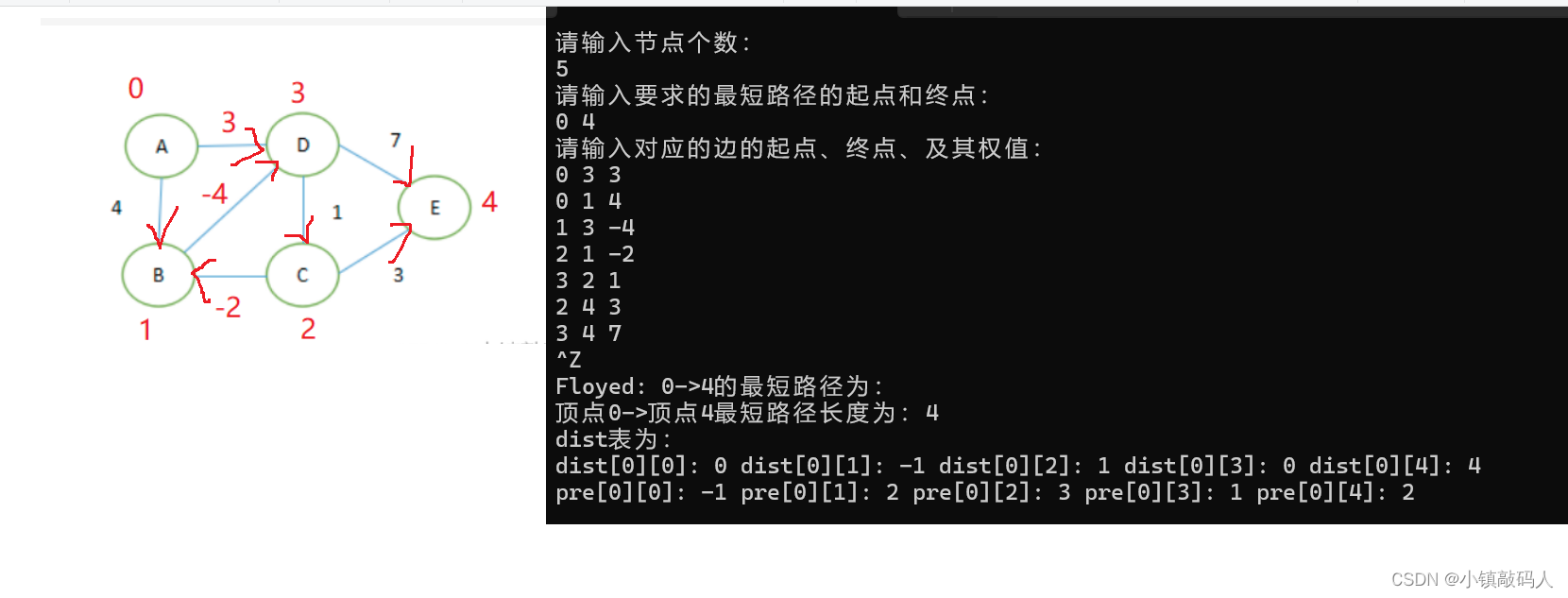
1.无向图,无负权。
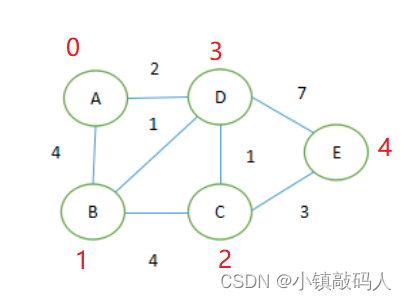
运行结果:
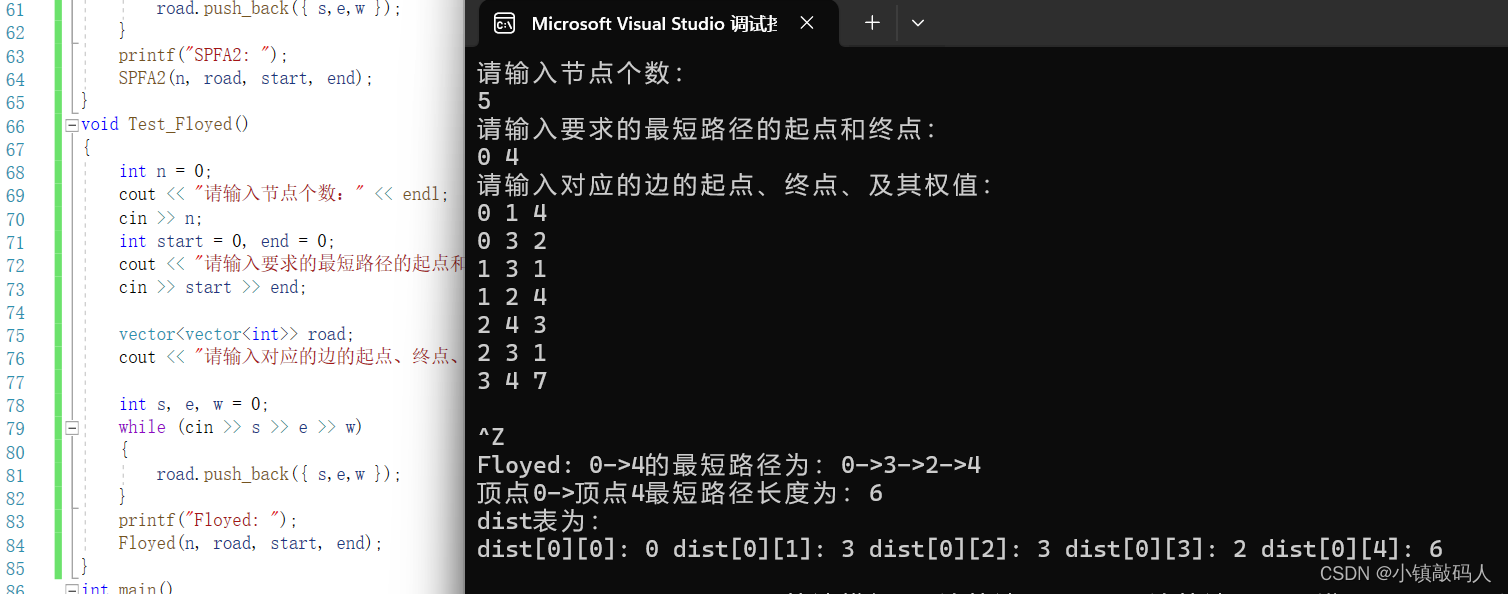
与预期结果一致。
- 有向图,有负权但是无负权回路。
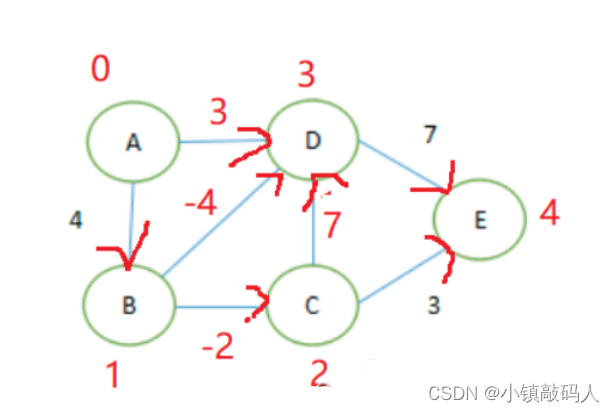
有向图记得修改代码为单向连通:
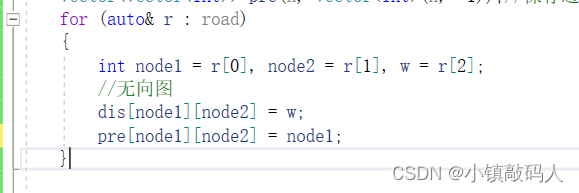
运行结果:
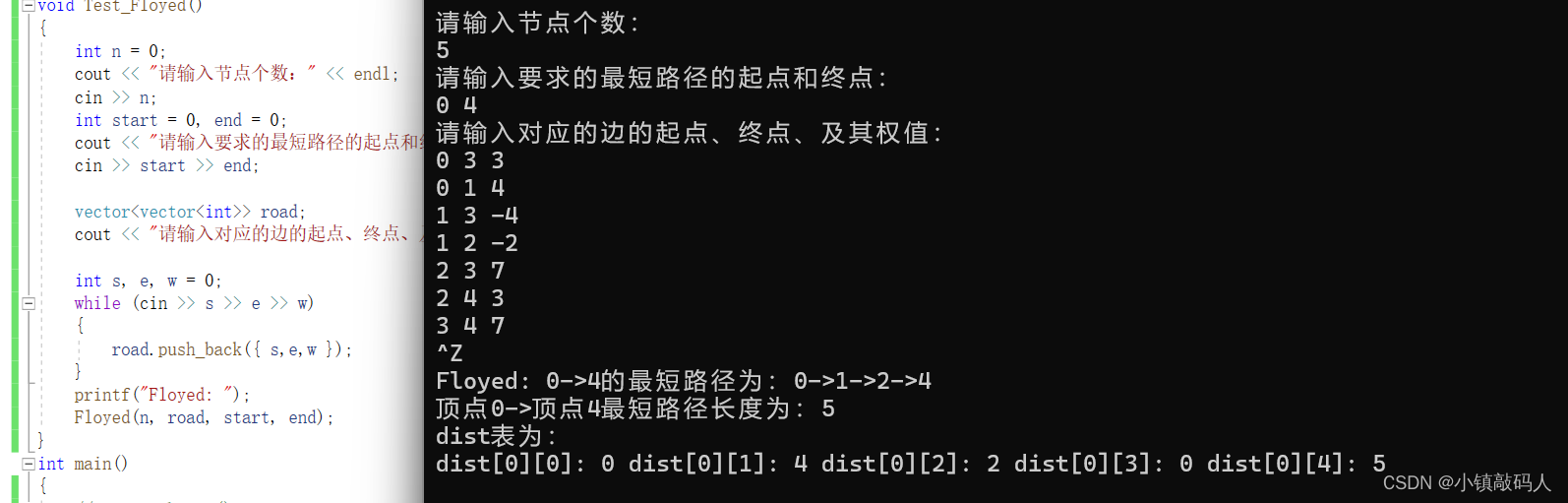
- 有向图,且存在负环,这个算法无法解决这个问题。
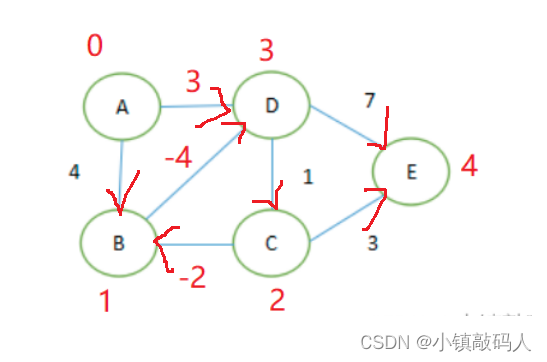
所以在打印的时候就出现了栈溢出这种问题:
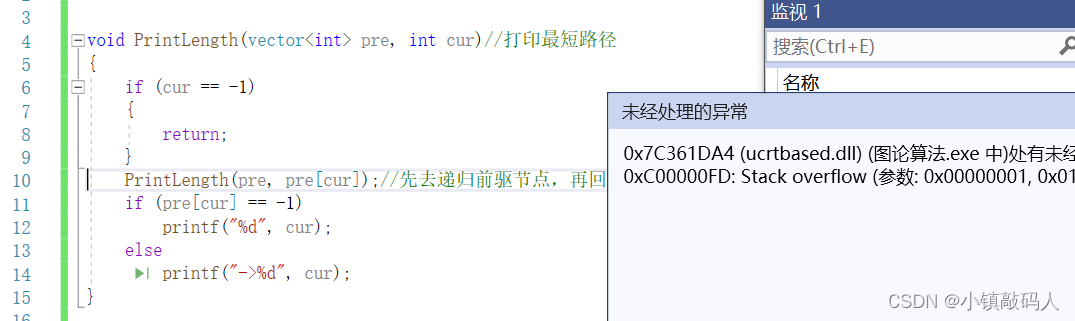
看打印结果可以知道,就是这个负环导致的:
🌕 OJ测试最短路径算法的正确性
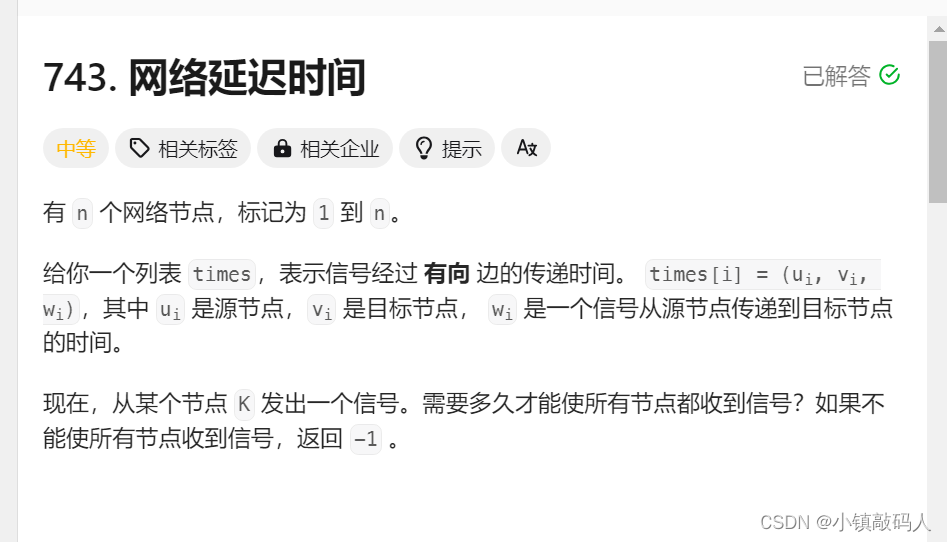
OJ题,点这里
这题是一个计算所有最短路径的最大值的题,如果不能保证起点和所有顶点都连通,就返回-1,注意这题有两个点需要注意:
1、有向图,边并非双向
2、顶点从1~n,所以我们需要多开一位的,防止数组越界。
🌰 Dijkstra1(未优化版本OJ测试)
我们在原先的代码上面做下微调就可以直接调用了:
ak代码:
class Solution {
public:
//我们这里处理的是无向图,如果是有向图微调即可
int Dijkstra1(int n, vector<vector<int>> road, int start, int end)//最短路算法,Dijkstra算法实现,返回顶点x到其它顶点的距离,road数组保存着每条边的开始的点,和结束的点以及它的权值
{
//首先我们需要初始化邻接表,因为road并不是,road只是每条边的信息
vector<vector<pair<int,int>>> G(n+1);//假设节点从0开始
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//有向图
G[node1].push_back({ node2,w });
}
vector<long long> dist(n+1, LLONG_MAX / 2);//dist数组存放起点start到每个节点之间的距离,一开始全部初始化为最大值的一半,为什么是一半呢?这里是防止溢出
dist[start] = 0;//start自己到自己的距离是0
vector<bool> find(n+1, false);//find数组是标记是否找到了节点start到i的最短路径
int min_i = -1;
while (1)
{
min_i = -1;
for (int i = 1; i <= n; ++i)
{
if (!find[i] && (min_i == -1 || dist[min_i] > dist[i]))
{
min_i = i;
}
}
if (min_i == -1)
break;
find[min_i] = true;//说明这个点已经找到了起点到它的最短路径,标记为true
//用这个最短路径的点去更新其它的点
for (auto& node:G[min_i])
{
long long newdis = node.second + dist[min_i];
if (newdis < dist[node.first])//如果比我现在的距离要小,就更新距离和上一个节点的下标
{
dist[node.first] = newdis;
}
}
}
long long ans = 0;
for(int j = 1;j < dist.size();++j)
{
ans = max(dist[j],ans);
}
if(ans == LLONG_MAX/2)
return -1;
else
return ans;
}
int networkDelayTime(vector<vector<int>>& road, int n, int start) {
return Dijkstra1(n,road,start,n);
}
};
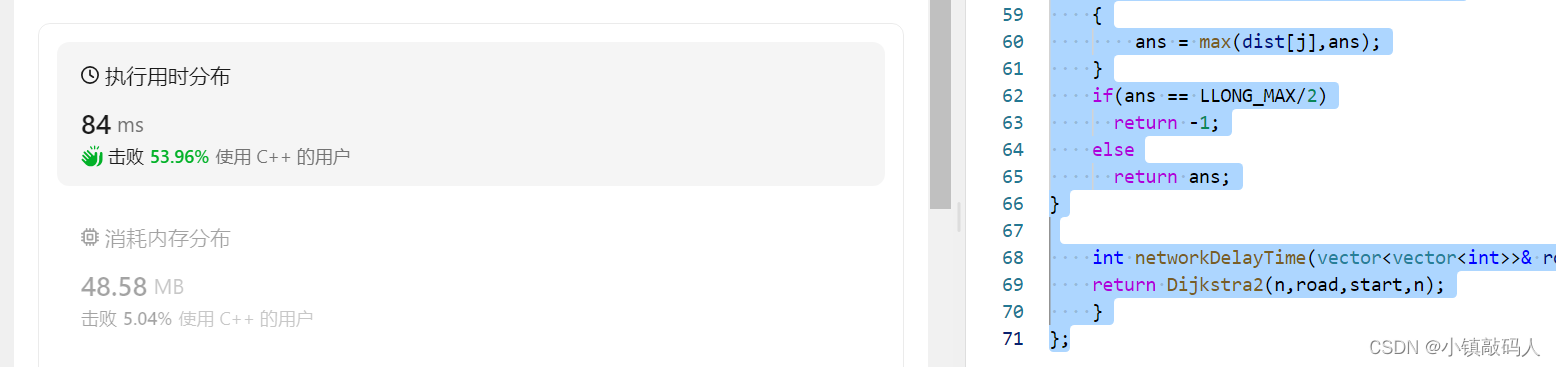
ak截图( O ( N 2 ) , 适合稠密图 O(N^2),适合稠密图 O(N2),适合稠密图):

🌰 Dijkstra2(优化版本OJ测试)
代码:
class Solution {
//内部类
private:
class my_compare
{
public:
bool operator()(pair<long long, int> a, pair<long long, int> b)
{
return a.first > b.first;
}
};
public:
//我们这里处理的是无向图,如果是有向图微调即可
int Dijkstra2(int n, vector<vector<int>> road, int start, int end)//最短路算法,Dijkstra算法实现,优先队列优化版本
{
//首先我们需要初始化邻接表,因为road并不是,road只是每条边的信息
vector<vector<pair<int, int>>> G(n+1);//假设节点从0开始
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//有向图
G[node1].push_back({ node2,w });
}
vector<long long> dist(n+1, LLONG_MAX / 2);//dist数组存放起点start到每个节点之间的距离,一开始全部初始化为最大值的一半,为什么是一半呢?这里是防止溢出
priority_queue<pair<long long, int>,vector<pair<long long,int>>,my_compare> q1;//创建一个小根堆,来更快的求出每次的最短路径
dist[start] = 0;//start自己到自己的距离是0
q1.push({ 0,start });//初始化
while (1)
{
int min_i = -1;
int dis_min = 0;
if (!q1.empty())
{
min_i = q1.top().second;
dis_min = q1.top().first;
q1.pop();//这个最短路径即将被用来更新其它节点,没有作用了,从优先队列中pop掉
}
if (min_i == -1)//求出起点到end的最短路径就满足要求了,退出程序
break;
if (dis_min > dist[min_i])//可能出现这种情况,就是这个节点的信息之前就已经存入队列中了,但是再次更新之后没有把旧的信息删除,就会造成这种不匹配的现象,我们跳过这种不合法的情况
continue;
//用这个最短路径的点去更新其它的点
for (auto& node : G[min_i])
{
long long newdis = node.second + dist[min_i];
if (newdis < dist[node.first])//如果比我现在的距离要小,就更新距离和上一个节点的下标
{
dist[node.first] = newdis;
q1.push({ newdis,node.first });
}
}
}
long long ans = 0;
for(int j = 1;j < dist.size();++j)
{
ans = max(dist[j],ans);
}
if(ans == LLONG_MAX/2)
return -1;
else
return ans;
}
int networkDelayTime(vector<vector<int>>& road, int n, int start) {
return Dijkstra2(n,road,start,n);
}
};
ak截图(稀疏图下为 N ∗ l o g N N*logN N∗logN):
🌰 Bellman-ford算法OJ测试
ak代码:
class Solution {
public:
int Bellman_ford(int n, vector<vector<int>> road, int start, int end)//单源算法可处理负权,假设是无向图
{
//我们还是使用邻接表保存每条边的信息,因为有时候是无向图,不会把双向的边都表示出来
vector<vector<pair<int,int>>> G(n+1);
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//有向图
G[node1].push_back({ node2,w });
}
vector<long long> dis(n+1,LLONG_MAX/2);//dis[i]表示顶点start到i的距离
dis[start] = 0;
for (int i = 0; i < n - 1; ++i)//n个节点,至多n-1次就可以求出最优路径
{
//枚举每条边
for (int j = 1; j <= n; ++j)
{
for (auto& k : G[j])
{
int x = k.first, w = k.second;
if (dis[j] + w < dis[x])//如果加j->x这条边,可以让dis[x]的值变小,就更新
{
dis[x] = dis[j]+w;
}
}
}
}
long long ans = 0;
for(int j = 1;j < dis.size();++j)
{
ans = max(dis[j],ans);
}
if(ans == LLONG_MAX/2)
return -1;
else
return ans;
}
int networkDelayTime(vector<vector<int>>& road, int n, int start) {
return Bellman_ford(n,road,start,n);
}
};
ak截图( O ( n m ) O(nm) O(nm)):
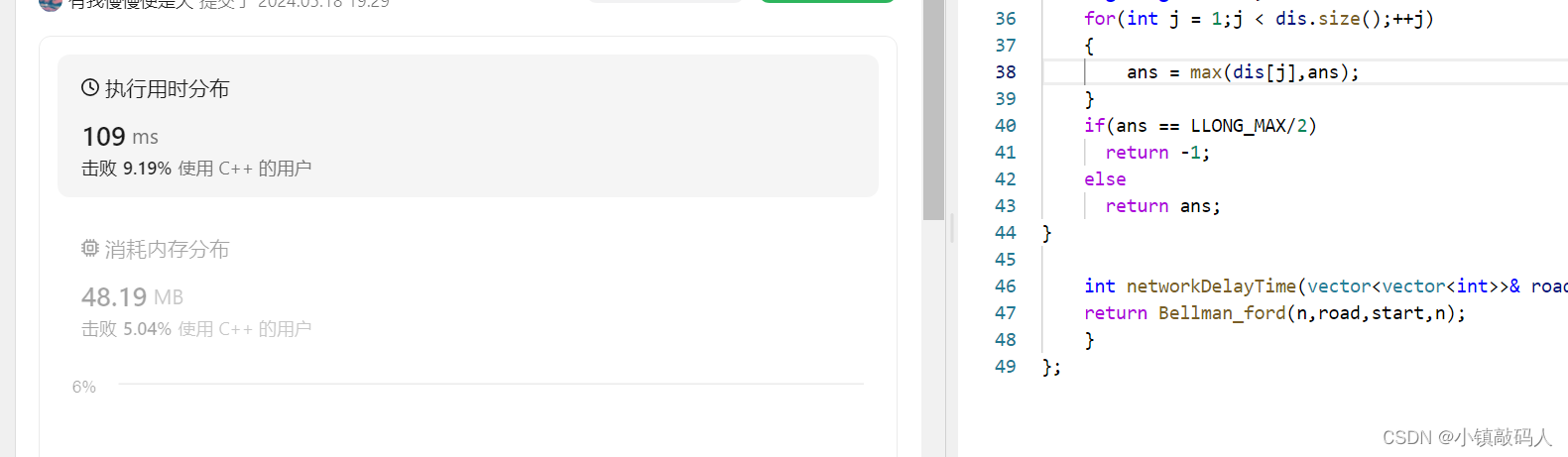
🌰 SPFA算法OJ测试
ak代码:
class Solution {
public:
int SPFA1(int n, vector<vector<int>> road, int start, int end)//假设是有向图
{
//我们还是使用邻接表保存每条边的信息,因为有时候是无向图,不会把双向的边都表示出来
vector<vector<pair<int, int>>> G(n+1);
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//有向图
G[node1].push_back({ node2,w });
}
vector<long long> dis(n+1, LLONG_MAX / 2);//dis[i]表示顶点start到i的距离
vector<bool> vis(n+1);//判断节点i是否在队列中,防止重复入队列
queue<int> q;
q.push(start);
vis[start] = true;
dis[start] = 0;
//开始松弛
while (!q.empty())
{
int i = q.front();//取队首节点
q.pop();
vis[i] = false;
for (auto& node : G[i])//更新i指向的顶点
{
int j = node.first, w = node.second;//加入i->j这条边是否能使,dis[j]变短,如果能更新dis[j]
if (dis[i] + w < dis[j])
{
dis[j] = dis[i] + w;
if(!vis[j])//如果j此时不在队列中
q.push(j);
vis[j] = true;
}
}
}
long long ans = 0;
for(int j = 1;j < dis.size();++j)
{
ans = max(dis[j],ans);
}
if(ans == LLONG_MAX/2)
return -1;
else
return ans;
}
int networkDelayTime(vector<vector<int>>& road, int n, int start) {
return SPFA1(n,road,start,n);
}
};
ak截图( O ( k m ) O(km) O(km)):

🌰 Floyed算法OJ测试
ak代码:
class Solution {
public:
int Floyed(int n,vector<vector<int>> road,int start,int end)//多源最短路算法可以处理负权,但是不能处理带有负环的图 N^3
{
vector<vector<long long>> dis(n+1, vector<long long>(n+1, LLONG_MAX / 2));//假设节点从0开始
for (auto& r : road)
{
int node1 = r[0], node2 = r[1], w = r[2];
//有向图
dis[node1][node2] = w;
}
//将对角线的距离都初始化为0
for (int i = 1, j = 1; i <= n; ++i,++j)
{
dis[i][j] = 0;
}
//使用每个节点作为中间节点,去更新新其它的节点
for (int k = 1; k <= n; ++k)
{
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
{
if (i == k)
break;
if (j == k || j == i)
continue;
if (dis[i][j] > dis[i][k] + dis[k][j])//用这个中间节点来更新
{
dis[i][j] = dis[i][k] + dis[k][j];
}
}
}
long long ans = 0;
for(int j = 1;j < dis[start].size();++j)
{
ans = max(dis[start][j],ans);
}
if(ans == LLONG_MAX/2)
return -1;
else
return ans;
}
int networkDelayTime(vector<vector<int>>& road, int n, int start) {
return Floyed(n,road,start,n);
}
};
ak截图( O ( N 3 ) O(N^3) O(N3)):

因为数据量比较小,所以看不出性能上的太大区别。
🌕 总结
| 最短路径算法 | 时间复杂度 | 是否能处理负权 | 是否能处理负环 | 单源/多源 |
|---|---|---|---|---|
| Dijkstra | O ( N ∗ l o g N ) O(N*logN) O(N∗logN)(使用小堆优化的版本,适合稀疏图), O ( N 2 ) ( 普通版本 , 适合稠密图 ) O(N^2)(普通版本,适合稠密图) O(N2)(普通版本,适合稠密图) | NO | NO | 单源 |
| Bellman_ford | O ( n ∗ m ) O(n*m) O(n∗m),m为边数,n为顶点数 | YES | YES | 单源 |
| SPFA | O ( k m ) O(km) O(km),m为边数,k为常数,通常为2。 | YES | YES | 单源 |
| Floyed | O ( N 3 ) O(N^3) O(N3) | YES | NO | 多源 |






















 425
425











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










