强化学习笔记（5）—— 无模型（model-free）prediction问题 （α-MC方法、TD方法）

• 参考：
  1. 周博磊老师的教程
  2. Reinforcement Learning Course by David Silver
  3. Richard S.Sutton 《Reinforce Learning》第5章、第6章
  4. 强化学习（四）用蒙特卡罗法（MC）求解
  5. 强化学习（五）用时序差分法（TD）求解
• 上一节我们探讨了环境MDP已知（model-based）情况下的 prediction 和 control 问题（强化学习笔记（3）—— MDP中的prediction和control问题）；本节主要讨论 MDP 未知时的prediction问题，MDP未知时的control问题下一篇再讨论
• 符号说明：本文用 $S_t$ 或 s 代表当前时刻 t 的状态，$S_{t+1}$ 或 s’ 代表下一时刻的状态；$A_t$ 或 a 代表当前时刻 t 的动作，$A_{t+1}$ 或 a’ 代表下一时刻的动作

---

1 引入

• 上一节我们探讨了解 prediction 问题的 policy evaluation 算法、解 control 问题的 policy iteration 和 value iteration 算法，它们都是 Model-based 方法，要求输入一个给定的 MDP（需要访问环境，包括状态转移矩阵和奖励函数）
• 但很多情况下 MDP 是未知的，这时核心问题就发生了变化
  1. Model-free prediction：Estimate value function of an unknown MDP
  2. Model-free control:：Optimize value function of an unknown MDP

1.1 回顾model-based prediction问题

1.1.1 policy evaluation算法

• 使用MDP的Bellman公式反复迭代计算至收敛
  
• 常使用DP方法实现这个迭代

1.1.2 小结

• 在MDP已知的情况下，Agent已经知道了环境的状态转移 $P$ 和状态奖励 $R$，即全观测（fully observable）。 这时Agent不需要再探索环境，直接利用 $P$ 和 $R$ 迭代求 $V^{\ast }$ 和 ${\pi }^{\ast }$ 即可 (上面红色的部分)，就好像玩游戏开了透视挂一样
  
• 但在对于很多问题，MDP要么未知，要么虽然已知但因为过于庞大/复杂而无法使用 （如电子游戏、无人机控制…）这些情况下状态太多，转移太复杂，没法给出P和R，也就无法进行iteration计算，这时就可以考虑使用model-free的强化学习方法

1.2 model-free RL

1. 无模型强化学习通过和环境进行交互来解决问题
   

2. Agent不能直接获取状态转移矩阵P和奖励函数R

3. Agent的每次交互过程，会采集一条轨迹（Trajectories/episodes），Agent要收集大量的轨迹，然后从中获取信息，改进策略，以求获得更多的奖励

4. 一条轨迹是一个 “状态、动作、奖励” 序列，如
   { S 1 , A 1 , R 2 , S 2 , A 2 , . . . S t , A t , R t + 1 , . . . R T , S T } \{S_1,A_1,R_2,S_2,A_2,...S_t,A_t,R_{t+1},...R_T,S_T\} {S1​,A1​,R2​,S2​,A2​,...St​,At​,Rt+1​,...RT​,ST​}

5. 下面介绍model-free RL的两种常用方法

   1. 蒙特卡罗方法（MC）：Monte Carlo Method
   2. TD学习方法 (TD) ：Temporal Difference Learning

2. Monte-Carlo Method（MC）Prediction

2.1 思想

• 以policy $\pi$ 大量进行轨迹采样，找到其中所有的状态 $s$，分别计算return $G_t$，用这些 $G_t$ 的期望（均值）作为 $s$ 的价值 $v^{\pi }(s)$

  1. Return： $G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...$ under policy $\pi$
  2. $v^{\pi }(s)={\mathbb{E}}_{\gamma ,\pi }[G_t|S_t=s]$

  根据大数定律，当采集的轨迹足够多时，$v(s)\to v^{\pi }(s)$

• 在MC方法中，定义

  1. MC target： $G_t$
  2. MC error：${\delta }_t=G_t-v(S_t)$ 我们利用它修正 $v(S_t)$

2.2 特点

1. MC 方法从经验中直接估算值函数 $V$ 和策略 $\pi$（learn directly from episodes of experience），使用经验平均return（empirical mean return）代替数学期望 return（expected return），因此当状态价值不随时间改变（即处于稳定情况stationary）时，轨迹采样越多学习效果越好

2. MC 方法是 model-free 的，不要求 MDP 的转移矩阵 $P$ 或奖励 $R$，不需要bootstrapping，甚至不假设状态具有 markov property

3. MC 需要的轨迹必须是 “经历完整的”（all episodes must terminate）。

   所谓的经历完整，就是这个序列必须要达到终止状态，比如下棋问题分出输赢，驾车问题成功到达终点或者失败

   因为 $V$ 的定义是 $v^{\pi }(s)={\mathbb{E}}_{\pi }[G_t|S_t=s]$，而 $G_t$ 的定义是episode中从第 $t$ 步到最后的奖励加权和，因此 episode 必须到终止状态，否则计算的就不是 $G_t$ 了，得出的不是状态 $s$ 的真正价值。换句话说，只有等到episode终止，我们才能反向计算 $G_t$ 并修正 $v(S_t)$

4. 只有在一个 episode 学完后，价值估计和策略才会改变。因此，MC方法在逐个完整轨迹的意义上是增量的（“episode by episode”），而不是在每个单步的意义上增量（not “step by step”），TD 学习可以做到后者

2.3 两类MC prediction方法

• episode中出现一次 “状态s/二元组(s,a)”，称为对 “状态s/二元组(s,a)” 的一次访问（visit）
• “状态s/二元组(s,a)” 可能在同一个episode中多次出现，以此可以把MC方法分成两类

2.3.1 首次访问型 MC

• first-visit MC：仅把状态序列中第一次出现该状态时的收获值纳入到 return 平均值的计算中
  
  • 这里用Returns这个list存储每个状态s从episode中提取的若干return $G_t$
  • 对于每个轨迹从后往前递推地计算$G_t$
  • Unless 可以理解为 if not，仅保留轨迹中状态s第一次出现时的return

2.3.2 每次访问型 MC

• every-visit MC：针对一个状态序列中每次出现的该状态，都计算对应的收获值并纳入到收获平均值的计算中
  • 这种方式的伪代码和上面的很像，只要把Unless判断那句去掉就行了
  • 这种方法比第一种的计算量要大一些，但是在完整的经历样本序列少的场景下会比第一种方法适用。

2.3.3 收敛性

• 当对 $s$ 或 $(s,a)$ 的访问次数足够大时，这两种方法都可以收敛到 $V^{\pi }$ 或 $Q^{\pi }$。
  1. 对于 first-visit MC方法来说，从每个 $s$ 或 $(s,a)$ 所在的episode中获取一个 return 作为对 $V$ 或 $Q$ 的估计，这些return以有限的方差服从i.i.d分布，根据大数定律，这些return的平均值收敛于它们的期望值。每个平均值本身是一个无偏估计，其误差的标准差为 $\frac{1}{\sqrt{N}}$ （N是return的数量）
  2. 对于 every-visit MC方法，这一点不是很直观。可以证明这种方法的估计会二次收敛到$V^{\pi }(s)$ (相关文章：Singh和Sutton, 1996)

2.4 增量式实现

• 看上面两种MC方法的伪代码，其中求均值的部分可以改成增量形式，这样就只需要保存上一轮迭代得到的收获均值与次数，无论数据量是多还是少，算法需要的内存基本是固定的
• 一个增量式求均值的推导如下
  

2.4.1 稳定情况（stationary）

• 当policy $\pi$ 固定时，$V$ 或 $Q$ 也不随时间变化，这时我们采集的episode越多，估计效果越好
• 以增量形式改写伪代码
  0. 前略…
  1. Collect one episode { S 1 , A 1 , R 2 , S 2 , A 2 , . . . S t , A t , R t + 1 , . . . R T , S T } \{S_1,A_1,R_2,S_2,A_2,...S_t,A_t,R_{t+1},...R_T,S_T\} {S1​,A1​,R2​,S2​,A2​,...St​,At​,Rt+1​,...RT​,ST​}
  2. 每次访问到状态$S_t$时，计算return $G_t$并以增量形式更新$V(S_t)$
     $$\begin{array}{rl}N(S_t)& \leftarrow N(S_t)+1\\ v(S_t)& \leftarrow v(s_t)+\frac{1}{N(S_t)}(G_t-v(S_t))\end{array}$$
     注意这里的$S_t$下标不代表迭代轮次，而是在代表轨迹中 t 时刻采样的这个状态s
• 如果要估计状态价值函数，方法完全类似，只要把更新V换成下面这个更新q即可
  $$q(S_t,A_t)\leftarrow q(S_t,A_t)+\frac{1}{N(S_t,A_t)}(G_t-q(S_t,A_t))$$

2.4.2 不稳定情况（nonstationary）

• 在真实的RL环境中，比如 Control 问题，我们往往要提升 Policy，这时策略评估和策略提升交替进行（Generalized Policy iteration）。面对一个不停变化的 Policy，$V,Q$ 也在随时间不断变化，我们采样的episode就不是越多越好了，因为越早期的采样的episode，其服从的Policy和当前相差越多，我们需要 “忘记” 一些太老的 $G_t$

• 一个常用的方法是设定一个均值计算步长，这有点像滑动均值滤波，我们只用最近若干次采样的 $G_t$ 来估计V(s)。设步长为n，并设$\frac{1}{n}=\alpha$，有
  $$\begin{array}{rl}v(S_t)& =\frac{1}{n}(G_t+(n-1)v(S_t))\\ & =\alpha (G_t+(\frac{1}{\alpha }-1)v(S_t))\\ & =v(S_t)+\alpha (G_t-v(S_t))\end{array}$$

  我们把 $\alpha$ 称为学习率，用来调节 $v(S_t)$ 的更新速度。$v(S_t)=v(S_t)+\alpha (G_t-v(S_t))$这个式子，可以直观地理解为我们不断地用新算出的 $G_t$ 来修正对 $v(S_t)$ 的估计，调整的多少由学习率 $\alpha$ 控制。这种方法一般称为 α-MC

• 如果要估计状态价值函数，方法完全类似，只要把更新V换成下面这个更新q即可
  $$q(S_t,A_t)\leftarrow q(S_t,A_t)+\alpha (G_t-q(S_t,A_t))$$

2.5 比较 MC 和 DP 算法

2.5.1 算法思想

1. DP方法中，使用了 自举（bootstrapping） 的思想，通过上一轮估计的 $V_{i-1}$ 来引导这一轮估计的 $V_i$，具体方法是在bellman等式上进行迭代
   

2. MC方法中，是使用来自大量采样轨迹的经验平均收益（empirical mean return）代替数学期望来估计 $V_i$。对于每个状态的估计是完全独立的，不依赖于对其他状态的估计（完全不使用bootstrapping的思想）
   

2.5.2 覆盖状态

1. 使用MC方法进行prediction时，不一定覆盖到 MDP 中所有的状态s。这是因为我们评估的是Policy $\pi$，通过不停执行这个策略来评估可以被 $\pi$ 覆盖到的状态的价值，对于那些Policy $\pi$没有涉及到的状态，其价值对于 prediction 问题没有意义，所以不需要考虑
2. 在DP方法中我们执行全宽度回溯，每轮迭代会计算所有状态的价值。对于Policy $\pi$ 没有涉及到的状态，虽然在 $P(s^{\prime }|s,a)=0$ 的限制下不会更新，但它们依然被考虑并计算，而MC根本不会处理到它们。

2.5.3 优缺点

1. MC相对DP的好处
   1. MC方法不需要知道 MDP，是一个Model- free的方法
   2. MC每轮更新只需要计算一条轨迹，其代价和状态数量、转移数量无关；而DP使用全宽度（full-width）的回溯机制更新行状态价值，每轮迭代需要计算并保存所有状态价值，这在状态多、转移复杂的情况下会非常慢
   3. 由于不使用自举的思想，每个状态的估计不依赖于其他状态的估计，当环境中马尔可夫性质不成立时，MC方法的性能损失较小
2. MC相对DP的缺点：
   1. 只能用在有有终止的 MDP 上 (each episode terminates)
   2. 每次采样都需要一个完整的状态序列。如果我们没有完整的状态序列，或者很难拿到较多的完整的状态序列，这时候蒙特卡罗法就不太好用了

3. Temporal-Difference Learning (TD) Prediction

3.1 思想

• 回顾MC方法，我们计算每个轨迹的episode的 $G_t$ ，并采用以下方式修正$V$的估计值
  $$v(S_t)\leftarrow v(s_t)+\frac{1}{N(S_t)}(G_t-v(S_t))$$ 使用类似 MRP 中的 Bellman 等式，$G_t$ 可以被分解成立即奖励和未来奖励两部分
  $$\begin{array}{rl}{G}_t& =R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...\\ & =R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+...)\\ & =R_{t+1}+\gamma G_{t+1}\end{array}$$根据 $V$ 的定义，有
  $$\begin{array}{rl}{v}^{\pi }(S_t)& ={\mathbb{E}}_{\pi }[G_t|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s]\\ & ={\mathbb{E}}_{\pi }[R_{t+1}+\gamma v^{\pi }(S_{t+1})|S_t=s]\end{array}$$

• 这启发我们用 $R_{t+1}+\gamma v(S_{t+1})$ 代替 MC 方法中的 $G_t$，也就是说

  1. MC 中，我们希望 $v_{\pi }(s)$ 和 $q_{\pi }(s,a)$ 靠近 $G_t$
  2. TD 中，我们希望 $v_{\pi }(s)$ 靠近 $r_{t+1}+\gamma v_{\pi }(s^{\prime })$；$q_{\pi }(s,a)$ 靠近 $r_{t+1}+\gamma q_{\pi }(s^{\prime },a^{\prime })$

  这个想法是合理的，以状态价值为例，$v_{\pi }(s)$ 和 $r_{t+1}+\gamma v_{\pi }(s^{\prime })$ 都是当前对真实价值的估计，有 $$\mathbb{E}[v_{\pi }(s)]=\mathbb{E}[r_{t+1}+\gamma v_{\pi }(s^{\prime })]$$ 而后者包含一个真实得到的奖励 $r_{t+1}$，因此比纯粹估计更准确一些，应当让估计朝着向它靠近的方向更新。另外，因为 TD 中的 episode 不完整没有对应次数N，使用 $\alpha \in [0,1]$ 作为修正步长。价值更新公式如下
  $$\begin{array}{rl}& v(S_t)=v(S_t)+\alpha [(R_{t+1}+\gamma v(S_{t+1}))-v(S_t)]\\ & q(S_t,A_t)=q(S_t,A_t)+\alpha [(R_{t+1}+\gamma q(S_{t+1},A_{t+1}))-q(S_t,A_t)]\end{array}$$ 用这两个代替 MC 方法中的价值更新公式，我们就得到了 TD(0)方法，也叫单步TD

• 在TD(0)中，定义

  1. TD target： $R_{t+1}+\gamma v(S_{t+1})$
  2. TD error：${\delta }_t=R_{t+1}+\gamma v(S_{t+1})-v(S_t)$ 我们利用它修正 $v(S_t)$

3.2 特点

• TD方法是一种介于MC和DP之间的算法
  1. TD方法直接通过采样的经验轨迹学习，因此不需要知道MDP的转移矩阵 $P$ 和奖励 $R$，是一个model-free的方法
  2. TD方法融合了 DP 中自举（bootstrapping）的思想，即利用当前的估计值来更新估计值。
• 相比于MC方法必须等到episode终止才能反向计算 $G_t$，TD(0)算法只需要等到下一个时刻确定 $S_{t+1}$ 后就可以立即进行一步更新。可以说MC的更新是 “episode by episode” 的离线策略，TD的更新是“step by step” 的在线策略。因此TD方法可以从不完整的轨迹（incomplete episodes）中学习

3.3 收敛性

• TD 方法使用了 bootstrapping 思想，从一个猜测中计算另一个猜测，而非等待实际的结果，这看起来有一点不可靠。幸运的是，我们已经证明了，对于任何策略 $\pi$ ，TD(0)都可以收敛到 $v_{\pi }(s)$ 或 $q_{\pi }(s,a)$。
  1. 如果使用一个足够小的步长 $\alpha$，那么它的均值能收敛到 $v_{\pi }(s)$ 或 $q_{\pi }(s,a)$
  2. 如果步长参数 $\alpha$ 根据下面这个随机近似条件逐渐变小，则它能以概率 1 收敛
     $$\sum _{n=1}^{\infty }{\alpha }_n(a)=\infty 且\sum _{n=1}^{\infty }{\alpha }_n^2(a)<\infty$$
• 大致来说
  • MC方法把 $G_t$ 作为估计目标。MC 得到的之所以是估计值而不是准确值，是因为每一条episode得到的 $G_t$ 都是一个定值，${\mathbb{E}}_{\pi }[G_t|S_t=s]$ 中这个期望不知道，只能通过大量采样，使用经验均值估计数学期望
  • TD方法把 $R_{t+1}+\gamma V(S_{t+1})$ 作为估计目标。TD方法得到的之所以是估计值而不是准确值，不是因为 ${\mathbb{E}}_{\Pi }[R_{t+1}+\gamma V^{\Pi }(S_{t+1})|S_t=s]$ 这里期望的原因。 TD方法一边和环境交互一边修正 $V$，采样 $S_{t+1}$ 时 MDP 环境中的转移矩阵 $P$ 和策略 $\pi$ 都发挥了作用，故每次更新使用的 TD error 都是概率采样的（不像MC方法中一样是固定值），可以说环境模型已经完整地提供了这个期望。真正的原因是 真实的 $v(S_{t+1})$ 不知道，所以只能用当前估计的 $v(S_{t+1})$ 来代替
• 注意到每次的 TD error ${\delta }_t$ 是当时所做估计的误差。因为TD误差取决于 $S_{t+1}$ 和 $R_{t+1}$，所以它实际上要到一个时间步骤之后才能得到。也就是说 ${\delta }_t$ 是 $V(S_t)$ 中的误差，在时间 $t+1$ 时可用。另外要注意的是，如果价值数组 $V$ 在一个episode中不发生变化（比如MC方法中就是如此），那么蒙特卡洛误差可以写成TD误差之和
  
  如果价值函数V在周期中被更新了（就像TD(0)中那样），那么这个等式就不准确，但是如果更新时的修正步长 $\alpha$ 很小，那么它仍然可以近似成立。这个等式的泛化在在推广在TD学习的理论和算法中起着重要作用

3.4 伪代码

• 下面给出TD(0)的伪代码
  

3.5 推广

• TD(0) / 单步TD 是一种最简单的特殊情况，它可以在两个方向扩展

  1. 所谓 单步TD，是指我们在更新之前只运行了一步，从状态$S_t$转移到状态$S_{t+1}$后就立刻进行更新。我们也可以在一次更新之前运行多步，这样的方法称作 n步TD，当n越来越大直到 $n=horizon$ 时，TD方法变为MC方法
     
  2. 所谓 TD(0)，括号里的这个0其实是一个超参数，它可以在$[0,1]$取值，扩展后的方法称为 TD(λ)

• 关于这两种扩展内容也比较多，后面再单独开写文章说明吧

4. 对比 MC 和 TD（prediction 角度）

4.1 示例 —— 开车回家

• 本例子出自 Richard S.Sutton 《Reinforce Learning》 第二版

• 每天当你下班开车回家时，你会估计一下回家需要多长时间。假设在这个星期五，你正好在6点钟离开，估计需要30分钟才能到家。当你到达你的车时，已经是6:05，你注意到开始下雨了。交通状况在雨中的速度往往比较慢，所以你重新估计从那时起需要35分钟，也就是总共40分钟。15分钟后，你按时完成了高速公路部分的行程。当你驶入一条二级公路时，你将你估计的总行程时间缩短到35分钟。不幸的是，此时你被一辆缓慢的卡车卡在后面，而且道路太窄，无法通过。最后你不得不跟着卡车走，直到6点40分转入你住的小街。三分钟后你到家了。这一条episode总结如下
  

• 在这个例子中，reward是每一段行程消耗的时间（如果这是一个求最短行程时间的控制问题，则我们会使用负的收益，但这里我们只考虑 prediction 问题，为了简单，我们使用正收益）。使用表格中 “经过的时间” 这一列中相邻两个值做差来计算R。比如下高速这个状态的奖励就是 30-20=10

• 过程的衰减系数 $\gamma =1$，即每个状态的return $G_t$ 是从此到家的剩余时间，可以用总时间 43 和第一列 “已经过时间” 做差计算。

• 每个状态的价值是从此到家的剩余时间的期望。

• 表格中 “估计剩余时间” 这一列即是刚进入此状态时获得的对 $v(s)$ 的估计值，用作TD中的 $v(S_{t+1})$、MC中的 $v(S_t)$

• 表格中 “估计总时间” 为同一行前两列的值相加，做差代表MC和TD方法的target error。这一点比较重要，不然下面的图可能会看不懂。请看下面的分析

• 现在分别使用1-MC方法和TD(0)方法对这个episode进行prediction，如下
  
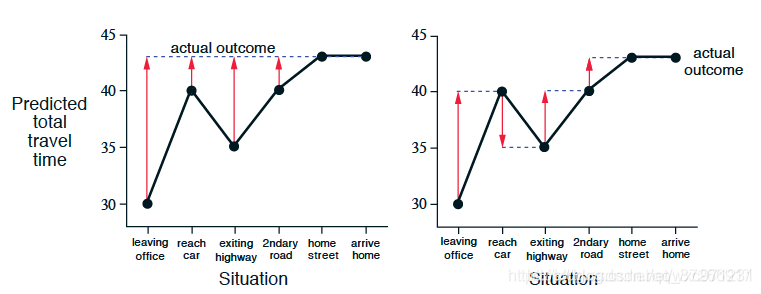
  图中左边是1-MC方法，右边是TD(0)方法。红色箭头表示两算法给出的对每个状态的价值修正值。

• 这个图画的有点难看懂，下面以 “下高速” 时刻为例进行解释。设 “下高速” 为状态 $S_t$，下一个状态 “被卡车挡住” 为状态$S_{t+1}$，最后到家为终态 $S_{end}$。有$R_{t+1}=30-20=10$，$G_t=43-20=23$。另外根据使用的方法，$\alpha =\gamma =1$

  1. 1-MC方法：
     $$\begin{array}{rl}V(S_t)& =V(S_t)+\alpha (G_t-V(S_t))\\ & =15+[(43-20)-15]\\ & =23\end{array}$$ 可见由于仅有一个episode，状态价值直接变为了这个episode中此状态的return $G_t$。图里的红色线，表现的是表格中状态$S_t$和$S_{end}$ 的第三列 “预测总时间” 的差值，而第三列又是前两列的和，把这个差转换为 (经过的时间+估计剩余时间$V(s)$) 的差，两个 “经过的时间” 做差算出的是$G_t$，而终止状态$S_{end}$的 “估计剩余时间” $V(S_{end})=0$，于是红线代表的就是 $G_t-V(s)$ 这个差值了，这正是MC方法的target error，即 “状态的价值修正值”

  2. TD(0) 方法：
     $$\begin{array}{rl}V(S_t)& =V(S_t)+\alpha [(R_{t+1}+\gamma V(S_{t+1}))-V(S_t)]\\ & =15+1\ast [10+1\ast 10-15]\\ & =20\end{array}$$ 图里的红色线，表现的是表格中状态$S_t$和$S_{t+1}$ 的第三列 “预测总时间” 的差值，而第三列又是前两列的和，同样把这个差转换为 (经过的时间+估计剩余时间$V(s)$) 的差，两个 “经过的时间” 做差算出的是$R_{t+1}$，于是红线代表的就是 $R_{t+1}+V(S_{t+1})-V(s)$ 这个差值了，这正是TD方法的target error，即 “状态的价值修正值”

• emmmm这个例子感觉真的不怎么好，尤其这个折线图画的不直观。不过我认为理解以下几个重点即可

  1. MC方法必须等到episode结束后，才能反向计算 $G_t$ 对 $v(s)$ 进行更新
  2. TD方法中状态每一步变化都可以立即对 $v(s)$ 进行更新，且更新时的修正值与预测值在时序上的变化，即时序的差分成正比（$\alpha$），这正是TD学习名称的由来（Temporal-Difference 即 “时序差分”）。
  3. 所谓 “预测值在时序上的变化”，可以从TD target error的角度理解：忽略折扣系数 $\gamma$ 和修正步长 $\alpha$，在时刻 $t$，我们估计状态 $S_t$ 的价值为 $v(S_t)$，在时刻 $t+1$，我们估计状态 $S_{t+1}$ 的价值为 $v(S_{t+1})$，也就是间接地估计状态 $S_t$ 的价值为 $R_{t+1}+v(S_{t+1})$，于是用预测的差分$R_{t+1}+v(S_{t+1})-v(S_t)$ 来修正 $v(S_t)$
  4. TD算法中涉及到 $R_{t+1}$ 和 $S_{t+1}$，在状态转移时获得奖励，这暗示着马尔可夫性，稍后我们详细分析这一点

• 这个例子啰啰嗦嗦讲的有点多，希望能给大家更多的观察角度

4.2 对比

4.2.1 基本特性

1. 相比 DP，TD 方法不需要模型的 $P$ 和 $R$，是一个 model-free 的方法
2. 相比 MC 方法必须等待一个episode完全终止后才能更新，TD方法在episode的每个时刻都可以更新（online）。这样的好处有以下几个
   1. 一些场景中，episode非常长，把更新推迟到整个轨迹结束后就太慢了，此时 MC 失效，只能用 TD
   2. 一些场景中可能是持续的任务（continuing environments, non-terminating），难以分出 episode 的概念。这时 MC 方法就会失效，而 TD 依然有效
   3. TD 方法可以从不完整的 episode 中学习，MC 则不行
   4. 有一些 MC 方法中，必须对那些采用实验性动作的 episode 进行折扣或干脆忽略掉，这可能大大减慢学习速度，而 TD 方法不太会受到这种影响

4.2.2 偏差和方差

1. 偏差（bias）对比

   • 对于 MC 来说，MC target，即状态 $S_t$ 的Return $G_t$ 是对 $S_t$ 价值 $v_{\pi }(S_t)$ 的一个无偏估计。MC方法收敛的结果是对价值的无偏估计
   • 对于 TD 来说，如果有一个 oracle 告诉我们 $S_{t+1}$ 的真实价值 $v_{\pi }(S_{t+1})$，则 TD target $R_{t+1}+\gamma v_{\pi }(S_{t+1})$是对 $S_t$ 价值 $v_{\pi }(S_t)$ 的一个无偏估计，但事实上我们不能获得 $S_{t+1}$ 的真实价值，只能用当前的估计值 $v(S_{t+1})$ 来代替，因此真实的TD target是对$S_t$ 价值的有偏估计。TD方法收敛的结果是对价值的有偏估计

2. 方差（variance）对比

   1. 对于MC来说，计算MC target（即return）时向后看了很多步，MC每一步都有随机性（return depends on many random actions, transitions, rewards）
   2. 对于TD来说，计算TD target时只往后看了一步（TD target depends on one random action, transition, reward），TD只引入了一步随机性
   3. 虽然MC和TD都会收敛，但引入随机性越多，会导致多次计算的结果间差距越大，即方差越大

3. 小结

   1. MC方差高于TD，但没有偏差
      1. 更好的收敛性能（Good convergence properties, even with function approximation）
      2. 对设定的初值不敏感
      3. 易于理解和使用
   2. TD方法的方差低于MC，有一些偏差
      1. 通常比MC更高效（收敛快）
      2. 只要合理地选择步长$\alpha$，TD(0) 也可以收敛到s的真实价值 $V_{\pi }$ (but not always with function approximation)
      3. 对初始值的设定更敏感
      4. 在一些特定情况下，TD 的偏差可能导致算法失效

4.2.3 收敛速度

• MC 和 TD哪个收敛更快？这还是一个开放性问题，没有人从数学上证明了某种方法比另一种更快地收敛，事实上我们甚至还不清楚如何恰当地形式化描述这个问题，不过在实际应用上，TD在随机任务上一般比α-MC更快收敛

• 下面看一个例子：随机游走

  • 本例子出自 Richard S.Sutton 《Reinforce Learning》 第二版

  • 我们在关注prediction问题时，因为不需要区分变化是环境引起的还是Agent动作引起的，所以经常会用到MRP。下面给出一个MRP，所有的事件都从中心状态C开始，然后在每一步上以相等的概率向左或向右移动一个状态。事件在极左或极右终止。当一个事件在右边终止时，会发生+1的奖励，其他奖励都是零。另外，这里衰减系数$\gamma =1$，不进行折扣。现在对这个MRP进行prediction任务
    
    易知，从A到E的价值分别是$\frac{1}{6},\frac{2}{6},\frac{3}{6},\frac{4}{6},\frac{5}{6},\frac{6}{6}$

  • 现在使用α-MC和TD(0)算法进行试验
    

  1. 左图反映了TD(0)在不同数量的采样episode上学习的结果，这里步长取 $\alpha =0.1$。如图所示，所有状态的价值被初始化为0.5，第一个episode只使V(A)下降，可以推出第一幕是终止在左边的终点。因为步长比较长，最终的结果会在True values附近震荡
  2. 右图给出了不同步长 $\alpha$ 下MC和TD(0)的表现，纵坐标指标是学得价值和真实价值的均方根误差（RMS），图中显示的是A到E五个状态RMS的平均值，并在100次运行下取平均的结果。这里同样把各个状态的初始价值设为0.5。

• 从右边的试验图可以看出

  1. TD比MC收敛更快
  2. 对于相同的方法，增大 $\alpha$ 可以加速收敛，但是曲线会更粗糙；减小 $\alpha$ 可以得到更光滑的曲线，但是收敛慢。
  3. $\alpha$ 决定了最终的收敛值在真实值附近波动的范围。$\alpha$ 越小，获得的结果越精确；如果选用的 $\alpha$ 太大，有可能不收敛

4.2.4 利用潜在的马尔可夫性

1. 批量更新（batch training）

   • 假设只有有限的episode，这时我们一般会反复地利用这些数据进行训练，直到得到的状态价值收敛为止。
   • 批量更新：向模型展示一整批 episode，期间不更新 $V$，只有当整批 episode 计算完之后，才根据所有 episode 得到的增量之和更新一次。
   • 使用批量更新的时候，只要步长参数$\alpha$足够小，TD(0) 就一定可以收敛到和 $\alpha$ 无关的唯一结果。α-MC 方法在同样的条件下也能确定地收敛，只是会收敛到和 TD(0) 不同的结果。下面我们通过分析二者得到结果的差异来深入理解 TD 和 MC 间的区别

2. 示例：批量更新的随机游走

   1. 这是 4.2.3 节讨论的随机游走示例的批量更新版本。每经过一个新的episode，所有到目前为止看到的episode都被视为一个批次。TD(0) 和 α-MC 不断地使用这些批次来更新，这里把 $\alpha$ 设定得足够小，保证二者都能收敛。下图绘制了两种方法求出的五个状态价值的均方根误差的均值（以整个实验的100次独立重复试验为基础）的学习曲线
      
      可以看到 TD(0) 方法的偏差值始终比MC方法更小

   2. 这个结果很奇怪，根据我们 4.2.2 节的分析，MC方法的修正完全基于训练数据，它最小化了与训练集中实际return的均方根误差，可以认为MC的结果是最优估计，但是图中批量TD方法居然在均方根误差上比MC表现得更好。

   3. 事实上，MC只是从某些有限的方面来说最优，TD方法的优越性某种程度上与prediction这个任务更相关。 这样说还是有点不清楚，先来看下面的这个例子

3. 示例：You are the Predictor

   1. 现在假设你观察到某个MRP的八个episode:

      A, 0, B, 0                           B, 1
      B, 1                                 B, 1
      B, 1                                 B, 1
      B, 1                                 B, 0
      

      解释一下，第1个episode从状态A开始，过渡到B，奖励为0，然后从B终止，奖励为0，其他7个情节更短，从B开始就立即终止并获得奖励了。给定这批数据，你认为V(A)和V(B) 的最优估计值是多少 ？

   2. 每个人都应该同意 $v(B)$ 的最优估计是0.75，因为这批数据在B结束了8次，其中6次return = 1，2次return = 0

   3. 但是对于 $v(A)$ 的估计值可以有两种看法

      1. 观察到过程在状态A时会以100%的概率转到状态B（获得0奖励），而B的价值为0.75，因此 $v(A)$ 的估计值应为0.75。这个答案本质上是先把这批 episode 建模成以下马尔可夫过程，再根据这个模型计算得出的。使用批量TD(0)会得到这个答案
         

      2. 简单地观察到 A 只出现了1次，获得的 return=0，因此认为 $v(A)$ 应当估计为0。使用批量MC会得到这个答案

   4. 分析两个方法计算的 $v(A)$ 估计值，不难看出 MC 的结果是在这批数据上均方误差最小的答案（实际上误差为0）。尽管如此，对于马尔可夫过程，我们仍然认为使用批量 TD(0) 得到的答案会在未来的数据上产生更小的误差

4. 分析

   1. 事实上，批量MC总是找出最小化训练集上均方误差的估计，而批量 TD(0) 总是找出完全符合马尔可夫过程模型的最大似然估计参数（使得生成的episode概率最大的参数）

   2. 在批量更新时，马尔可夫模型的最大似然估计参数可以从多个episode中通过频率推测出来
      
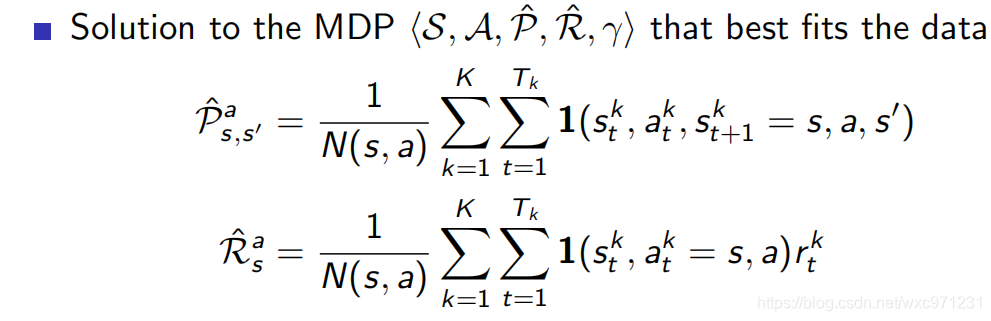
      如果在某批episode中估计出的model是正确的，则这一批的估计也就完全正确，这种估计称为 “完全等价估计”，因为它等价于假设潜在过程参数的估计是确定性的而不是近似的，批量TD(0)的收敛结果就是确定性等价估计

   3. 这一点也有助于理解为何 TD 比 MC 收敛得更快，在以批量形式学习的时候，TD(0) 比 MC 更快收敛是因为它计算的是真正的确定性等价估计。对于非批量 TD，尽管它不能通过频率推测出模型参数，不能达到确定性等价估计或最小均方误差估计，但它仍然大致地朝着这些方向在更新，因此它也往往比 α-MC 更快。

   4. 最后还要说明一点，尽管确定性等价估计在某种程度上是一个最优答案，但是直接计算它的复杂度太大了。如果有n个状态，仅仅建立最大似然估计就需要$n^2$的内存，按照传统方法计算V的复杂度达到 $o(n^3)$。相比之下，TD方法可以用不超过n的内存，通过在训练集上反复计算逼近同样的答案，这一优势是惊人的。对于状态空间巨大的任务，TD方法可能是唯一可行的逼近确定性等价解的方法

5. 总之，如果面对一个马尔可夫环境，由于 TD 方法的特殊的 TD target 设计，利用到相邻的状态价值 $v(S_{t+1})$ 和$R_{t+1}$，它可以充分挖掘环境的马尔可夫性并加以利用，因此TD在马尔可夫环境中更有效（more efficient），但相应的，如果环境中马尔可夫性不成立，TD受到的性能损失比MC大

5. q(s,a) 的 prediction

5.1 评估 q(s,a) 的重要性

• 假如我们现在对 $V(s)$ 进行评估并得到了最优价值函数 $V^{\ast }(s)$，如何从中得到最优策略 ${\pi }^{\ast }$ 呢

  1. 上一篇文章中我们在model-based情况下讨论了这个问题，这正是Policy iteration算法的最后一步。见：强化学习笔记（3）—— MDP中的prediction和control问题：在MDP已知时，我们可以往前看一步找到 $q^{\ast }(s,a)$，然后对它进行贪心找到使 $q^{\ast }(s,a)$ 最大的动作，即为状态 $s$ 下的最优策略。即
     $$\begin{array}{rl}{q}^{\ast }(s,a)& =R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\ast }(s^{\prime })\\ {\pi }^{\ast }(s)& =\underset{a\in A}{\mathrm{argmax}}{q}^{\ast }(s,a)\end{array}$$

  2. 然而，这里用到了 MDP 的转移矩阵P和奖励函数R，在model-free的情况下没法用这个方法

• 根据上述分析，在model-free的情况下，评估 $q_{\pi }(s,a)$ 往往比评估 $V_{\pi }(s)$ 更有用一些，这样我们就可以直接收敛到 $q^{\ast }(s,a)$，并在其上贪心得到最优策略 ${\pi }^{\ast }(s)$，这在下一篇文章讨论的 model-free control 问题中非常重要

5.2 评估方法

• 无论MC还是TD，$q(s,a)$ 的 prediction 思路都和 $v(s)$ 的 prediction 思路完全类似，核心的更新公式如下
  $$\begin{array}{rl}MC方法：q(S_t,A_t)& =q(S_t,A_t)+\alpha (G_t-q(S_t,A_t))\\ TD方法：q(S_t,A_t)& =q(S_t,A_t)+\alpha [(R_{t+1}+\gamma q(S_{t+1},A_{t+1}))-q(S_t,A_t)]\end{array}$$ 当对每个 $(s,a)$ 二元组的访问次数趋向无穷时，这两个方法都能二次收敛到 $q(s,a)$ 的真实期望值

5.3 保持试探问题

1. $q_{\pi }(s,a)$ prediction的一个特殊之处在于：有一些 $(s,a)$ 二元组可能永远不会被访问到。如果 $\pi$ 是一个确定性策略，那么遵循 $\pi$ 意味着在每一个状态 $s$ 中只能观测到一个动作 $a$ 的回报，这个状态对应状态集中的其他动作始终不能被选取，因而无法采样求平均。这个问题非常严重，因为学习 $q(s,a)$ 就是为了帮助在每个动作的所有可用动作间进行选择，进而为提升策略 $\pi$ 打下基础。
2. 相比而言，$v_{\pi }(s)$ prediction中也有一些状态 $s$ 可能覆盖不到，但是这个问题就不重要，因为对 $v_{\pi }(s)$ 进行评估仅仅就是在进行prediction而已，那些没有被 $\pi$ 覆盖的状态对于评估策略 $\pi$ 没有意义。而 对$q_{\pi }(s,a)$ 做 prediction 往往是为了优化 $\pi$ 进行的准备工作，我们必须试探所有动作，这样才能从中找出更好的动作以优化 $\pi$。在下一篇关于model-free control的文章中，我们还会回来强调这个问题。
3. 通常有两个方法可以解决此问题
   1. 试探性出发：将指定的 $(s,a)$ 二元组作为起点开始一个episode的采样，并且保证所有 $(s,a)$ 二元组都有非零的概率可以被选为起点。这保证了episode数量趋于无穷时，每个 $(s,a)$ 二元组都会被访问到无数次。这个方法通常很有效，但是在从真实环境中学习时，这个假设往往难以满足
   2. 只考虑那些在每个状态下所有动作都有非零概率被选中的随机策略，这样就从源头上避免了不可能被访问的 $(s,a)$ 的出现

6. 总结

6.1 DP、MC、TD(0) 对比图示

1. MC：每次更新按一条episode走到底，得到 $G_t$ 以进行修正
   
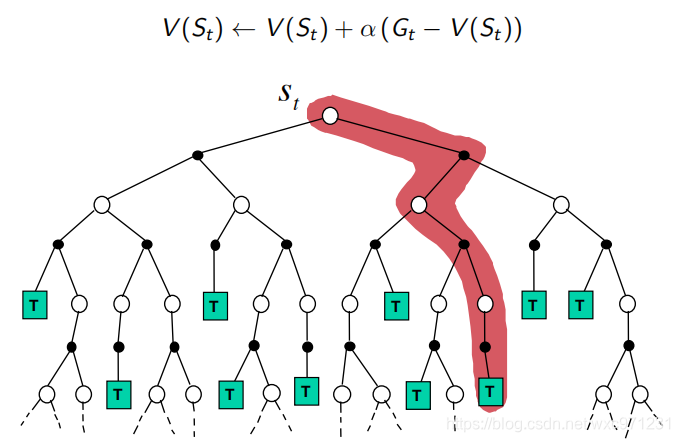
2. TD：每次更新只向前走一步，得到 $R_{t+1}$和$S_{t+1}$ 以进行修正
   
3. DP：每次更新只向前走一步，按概率得到所有可能的 $R_{t+1}$和$S_{t+1}$，计算期望以进行修正
   

6.2 Sampling & Bootstrapping

• Bootstrapping: update involves an estimate
  1. MC does not bootstrap
  2. DP bootstraps
  3. TD bootstraps
• Sampling: update samples an expectation
  1. MC samples
  2. DP does not sample
  3. TD samples

6.3 RL的统一观点

• 从TD按宽度扩展，即得DP；从TD按深度扩展，即得MC；同时按宽度和深度扩展，即得穷举搜索