KMP算法 - 深入浅出

最新推荐文章于 2023-09-26 00:27:35 发布

行云_

最新推荐文章于 2023-09-26 00:27:35 发布

阅读量1k

点赞数

分类专栏：算法

算法专栏收录该内容

7 篇文章 0 订阅

订阅专栏

原理

在朴素算法中，移动模式串后，就会丢掉之前已匹配符号的信息。所以，很可能一个文本符号会与不同的模式符号进行多次比较。这导致了最坏时间复杂度O(nm)（n:文本长度，m: 模式长度）。

KMP算法利用之前的符号比较信息。该算法不会对已经与某个模式符号匹配的文本符号进行重复比较。所以KMP的时间复杂度是O(n)。

然而，需要对模式串进行预处理以分析它的结构。预处理阶段的时间复杂度是O(m)。因为m<=n，所以总的时间复杂度是O(n)。

基本定义

定义：设A是一个字母表，x =x₀ ...x_k_-1,k∈ N 是一个由A中的字母构成的长度为k的字符串。

x的一个前缀是一个子串u：

u =x₀ ...x_b_-1 whereb∈{0, ...,k}

x的一个后缀是一个子串u:

u =x_k_-_b ... x_k_-1 whereb∈{0, ...,k}

如果u≠x,例如u的长度b小于k，则u分别叫做真前缀或真后缀。

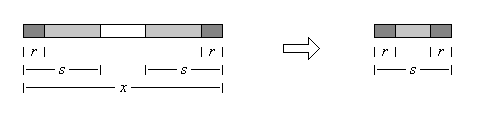
x的边界串(border)是一个子串r:

r =x₀ ...x_b_-1 and r =x_k_-_b ... x_k_-1 where b∈{0, ...,k-1}

x的边界是一个真前缀也是一个真后缀。它的长度b称为边界宽。

实例：设x=abacab，那么x的真前缀包括：

ε（空串）,a, ab, aba, abac, abaca

x的真后缀包括：

ε（空串), b, ab, cab, acab, bacab

ε长度为0，边界串ab长度为2

空串ε是所有非空字串的边界串。空串本身没有边界串。

下面的例子演示如何用边界串概念来确定移动距离。

实例：

0	1	2	3	4	5	6	7	8
a	b	c	a	b	c	a	b	d
a	b	c	a	b	d
			a	b	c	a	b	d

在0...4位置的符号已经匹配了，在位置5对c和d进行比较，发现不匹配。模式串可以被移动3个位置，然后继续在

位置5进行比较。

移动距离由模式串p的匹配前缀的最宽边界串决定。在这个例子中，匹配前缀是abcab，它的长度j=5,

它的最宽的边界串是ab，其宽度b等于2，移动距离等于j-b=5-2=3.

模式串的每个前缀的最宽边界串会在预处理阶段确定下来。这样，在随后的搜索阶段，移动距离就可以通过已经匹配的前缀计算出来。

预处理

定理：假设r, s 是x的边界串，并且|r| < |s|。那么r是s的边界串。

证明：如下图所示，r和s是字串x的边界串。因为r是x的前缀，所以它也是s的真前缀，因为它比s短。

因为r是x的后缀，所有r也是s的真后缀。因此r是s的边界串。

如果s是x的最宽的边界串，那么次宽的边界串r就是s的最宽的边界串。

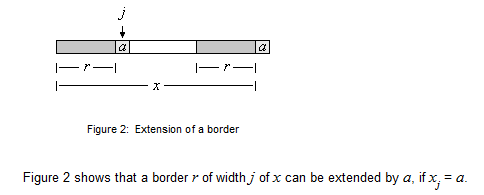
定义：设x是一个字串，a是A中的一个符号。如果ra是xa的一个边界串，x的边界串r就能够通过a进行扩展。

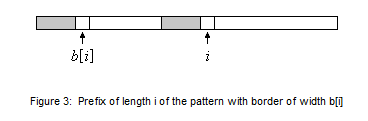
在预处理阶段会计算一个长度为m+1的数组，每一个元素b[i]包含模式串的长度为i的前缀的最宽边界串的

长度（i=0, ..., m)。因为长度为0的前缀ε没有边界串，我们设置b[0]=-1.

假如b[0], ..., b[i]的值已经知道了，那么b[i+1]的值可以通过检查前缀p₀ ...p_i-1的边界串是否可以被符号p_i扩展来计算。

如果p_b[i] =p_i就表示可以扩展（图3）。被检查的边界串可以通过递减顺序使用值b[i], b[b[i]]等获得。

预处理算法由一个变量j构成，j记录着这些值（上述的b[i], b[b[i]]）。如果p_j =p_i，则宽度为j的边界串就可以被p_i扩展。

否则，通过设置j = b[j]. 来检查次宽的边界串。如果没有边界串可以被扩展（j=-1）则循环终止。

通过语句j++递增j后，j就是p₀ ... p_i的最宽边界串的宽度，这个值被写入b[i+1]中

//Preprocessing algorithm
void kmpPreprocess()
{
    int i=0, j=-1;
    b[i]=j;
    while (i<m)
    {
        while (j>=0 && p[i]!=p[j]) j=b[j];
        i++; j++;
        b[i]=j;
    }
}

实例：对于模式 p = ababaa 数组b中的边界串的宽度有如下值。例如b[5]=3,因为前缀ababa有一个宽度为3的边界串。

`j`:	0	1	2	3	4	5	6
`p`[`j`]:	a	b	a	b	a	a
`b`[`j`]:	-1	0	0	1	2	3	1

搜索算法

从概念上讲，如上预处理算法可以被应用于字串pt而不仅仅是p。如果只计算最大宽度为m的边界串，

那么pt的某个前缀x的宽度为m的边界串相应的就对应与t中的一个模式匹配（假设边界串没有叠加）（Figure 4)。

这解释了，预处理算法和如下搜索算法的相似性。

//Searching algorithm
void kmpSearch()
{
    int i=0, j=0;
    while (i<n)
    {
        while (j>=0 && t[i]!=p[j]) j=b[j];
        i++; j++;
        if (j==m)
        {
            report(i-j);
            j=b[j];
        }
    }
}

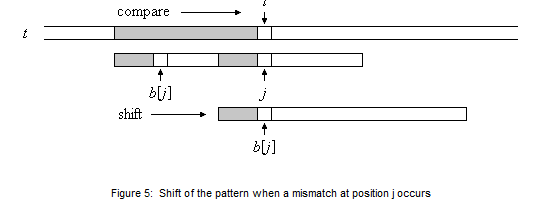
在内部的while循环中，当在位置j发生一个不匹配时，接着考虑长度为j的当前匹配前缀的最宽边界串（Figure 5)。

在位置b[j]继续比较，根据边界串的宽度，移动模式串。如果又发生了一个不匹配，那么就接着考虑次宽的边界串，

以此类推，直到没有边界串（j=-1）或者下一个符号匹配了。内部循环终止后，我们就有了一个新的模式串的当前

匹配前缀，接着继续执行外部循环。

如果模式串的m个符号都已经匹配了对应的文本窗口(j=m)，函数report就会被调用以报告匹配位置i-j。

随后，模式串被移动最宽边界串允许的最大距离。

下面的例子展示了搜索算法执行的比较，绿色表示匹配，红色表示不匹配。

实例：

0	1	2	3	4	5	6	7	8	9	...
a	b	a	b	b	a	b	a	a
a	b	a	b	a	c
		a	b	a	b	a	c
				a	b	a	b	a	c
					a	b	a	b	a	c
							a	b	a	b	a	c

分析

在预处理算法的内部循环中，j的递减值至少是1，因为b[j]<j。当j=-1时，循环终止，因此循环中所递减的j的值最多不超过

由语句j++增加的值。因为j++在外循环中执行了m次，所以内循环的总的执行次数不会超过m次。因此预处理算法的时机复杂

度为O(m)。

类似的分析可知搜索算法的时间复杂度为O(n)。上面的例子说明：比较形成了一个阶梯形状（红色和绿色符号）。整个

楼梯的高度顶多和宽一样，所以最多执行2n次比较。

因为m<=n，所以KMP总的复杂度是O(n)。

其中一种实现

void kmpPreprocess(const char *p, int *b)
{
	int i=0, j=-1;
	b[i] = j;
	int m=strlen(p);
	while(i<m)
	{
		while(j>-1 && p[j] != p[i]) j=b[j];
		i++; j++;
		b[i] = j;
	}
}
/** 
 *@return 匹配则返回匹配位置，否则返回-1
*/
int kmpSearch(const char *t, const char *p)
{
	int m=strlen(p);
	int *b = new int[m+1];
	kmpPreprocess(p, b);
	int n=strlen(t);
	int i=0, j=0;
	
	while(i<n)
	{
		if (t[i] == p[j] || j==-1) { i++; j++;}
		else
			j = b[j];
		if (j==m)
		{
			delete [] b;
			return i-j;
		}	
	}
	delete [] b;
	return -1;
}

另一种实现

//Searching algorithm
int kmpSearch2(const char *t, const char *p)
{
	int m=strlen(p), n=strlen(t);
	int *b = new int[m+1];
	kmpPreprocess(p, b);
	int i=0, j=0;
	while (i<n)
	{
		while (j>=0 && t[i]!=p[j]) j=b[j];
		i++; j++;
		if (j==m)
		{
			return (i-j);
			j=b[j];
		}
	}
	return -1;
}

原文：http://www.iti.fh-flensburg.de/lang/algorithmen/pattern/kmpen.htm