R型聚类分析是聚类分析的一种,一般对指标进行分类。
在实际工作中,为了避免漏掉某些重要因素,往往在一开始选取指标的时候尽可能考虑所有的相关因素,而这样做的结果,则是变量过多,变量间的相关度较高,给统计分析与建模带来极大不便,因此人们希望能够研究变量间的相似关系,按照变量的相似关系把他们聚合成若干类,进而找出影响系统的主要因素,引入了R型聚类方法。
方便自己比赛,写之。
举例:
服装标准制定中的变量聚类法:
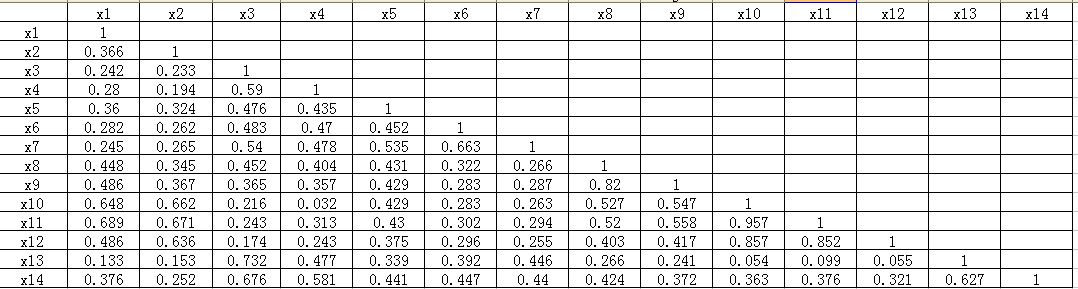
以下表格是女子14个部位的测量资料,各部位的相关系数表,其中,x1为上身长,x2位手臂长,x3为胸围,x4为颈围,x5为总肩宽,x6为总胸宽,x7为后背宽,x8为前腰节高,x9为后腰节高,x10为全身长,x11为身高,x12为下身长,x13为腰围,x14为臀围。
计算Matlab程序如下:
%把下三角相关系数矩阵粘贴到纯文本文件ch.txt中
clc,clear
a=textread('ch.txt');
d=1-abs(a); %进行数据变换,把相关系数转化为距离
d=tril(d); %提出d矩阵的下三角部分
b=nonzeros(d); %去掉d中的0元素
b=b'; %化成行向量
z=linkage(b,'complete'); %按最长距离法聚类
y=cluster(z,'maxclust',2);%把变量划分成两类,注:也可3类,底下记得修改
ind1=find(y==1); %显示第一类对应的变量编号
ind2=find(y==2); %显示第二类对应的变量编号
ind1=ind1';
ind2=ind2';
h=dendrogram(z); %画聚类图
ind1,ind2
set(h,'Color','k','LineWidth',2.0);%把聚类图线的颜色修改成黑色,线宽加粗聚类结果:
ind1 = 1 2 8 9 10 11 12
ind2 = 3 4 5 6 7 13 14
可以看出,人体变量大体可以分为两类:一类反应人体高矮的变量,一类反应人体胖瘦的变量。
~end~
待会再弄一个比较综合店的题目,Q型和R型方法都用到的。
























 541
541

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








