数组--螺旋矩阵

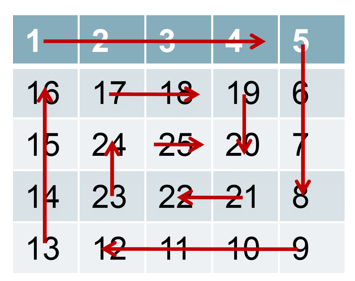
实现的方法由很多种，此处仅按层模拟法。

核心思想

将矩阵想象成一个洋葱，从最外层开始，一层一层地向内填充数字，每一层都按照 "上→右→下→左" 的顺序填充。

关键变量说明

c

int left = 0, right = n - 1;    // 当前层的左右边界
int top = 0, bottom = n - 1;    // 当前层的上下边界
int num = 1;                    // 当前要填充的数字

填充过程的详细分解

步骤1：填充上层（从左到右）

text

初始状态：left=0, right=3, top=0, bottom=3

   left     right
    ↓         ↓
top → [ 1   2   3   4 ]
      [              ]
      [              ]
      [              ]

代码执行：

c

for (int i = left; i <= right; i++) {
    matrix[top][i] = num++;
}
top++;  // 上边界下移

步骤2：填充右层（从上到下）

text

当前状态：left=0, right=3, top=1, bottom=3

      [ 1   2   3   4 ]
top → [           ↑   5 ]
      [           ↑   6 ]
      [           ↑   7 ]
               right

代码执行：

c

for (int i = top; i <= bottom; i++) {
    matrix[i][right] = num++;
}
right--;  // 右边界左移

步骤3：填充下层（从右到左）

text

当前状态：left=0, right=2, top=1, bottom=3

      [ 1   2   3   4 ]
      [           ↑   5 ]
      [           ↑   6 ]
bottom→ [ 10   9   8   7 ]
         ←────────┘

代码执行：

c

for (int i = right; i >= left; i--) {
    matrix[bottom][i] = num++;
}
bottom--;  // 下边界上移

步骤4：填充左层（从下到上）

text

当前状态：left=0, right=2, top=1, bottom=2

      [ 1   2   3   4 ]
top → [ 11   ↑       5 ]
      [ 10   ↑       6 ]
      [  9   8       7 ]
      ↑
    left

代码执行：

c

for (int i = bottom; i >= top; i--) {
    matrix[i][left] = num++;
}
left++;  // 左边界右移

完整循环过程演示（4×4矩阵）

第一层循环：

text

初始: [ .   .   .   . ]
      [ .   .   .   . ]
      [ .   .   .   . ]
      [ .   .   .   . ]

步骤1: [ 1   2   3   4 ]  ← 上边
      [ .   .   .   . ]
      [ .   .   .   . ]
      [ .   .   .   . ]

步骤2: [ 1   2   3   4 ]  ← 上边
      [ .   .   .   5 ]   ← 右边
      [ .   .   .   6 ]   ↑
      [ .   .   .   7 ]   ↑

步骤3: [ 1   2   3   4 ]  ← 上边
      [ .   .   .   5 ]   ← 右边
      [ .   .   .   6 ]   ↑
      [ 10  9   8   7 ]   ← 下边

步骤4: [ 1   2   3   4 ]  ← 上边
      [ 11  .   .   5 ]   ← 右边
      [ 10  .   .   6 ]   ↑
      [ 9   8   7   . ]   ← 下边

第二层循环：

text

当前: [ 1   2   3   4 ]
      [ 11  .   .   5 ]
      [ 10  .   .   6 ]
      [ 9   8   7   . ]

步骤1: [ 1   2   3   4 ]
      [ 11  12  13  5 ]  ← 上边(内层)
      [ 10  .   .   6 ]
      [ 9   8   7   . ]

步骤2: [ 1   2   3   4 ]
      [ 11  12  13  5 ]
      [ 10  .   .   6 ]
      [ 9   8   7   . ]
              ↑ 右边(内层) - 无空间

步骤3: [ 1   2   3   4 ]
      [ 11  12  13  5 ]
      [ 10  15  14  6 ]  ← 下边(内层)
      [ 9   8   7   . ]

步骤4: [ 1   2   3   4 ]
      [ 11  12  13  5 ]
      [ 10  15  14  6 ]
      [ 9   8   7  16 ]  ← 左边(内层) - 无空间

边界条件的重要性

c

if (top <= bottom) {
    // 填充下边 - 确保还有行需要填充
}

if (left <= right) {
    // 填充左边 - 确保还有列需要填充
}

这些条件防止在奇数×奇数矩阵的最后阶段重复填充。

算法特点

1. 时间复杂度：O(n²) - 每个元素只访问一次

2. 空间复杂度：O(1) - 只用了几个辅助变量（不包括结果矩阵）

3. 稳定性：逻辑清晰，不容易出错

4. 适用性：适合各种大小的方阵

这种方法的优势在于它的直观性和可预测性，通过维护四个边界指针，清晰地定义了每一层的填充范围。

#include <stdio.h>

void spiralMatrix(int n) {
    int matrix[n][n];
    int num = 1;
    int left = 0, right = n - 1;
    int top = 0, bottom = n - 1;

    while (left <= right && top <= bottom) {
        // 从左到右填充上边
        for (int i = left; i <= right; i++) {
            matrix[top][i] = num++;
        }
        top++;

        // 从上到下填充右边
        for (int i = top; i <= bottom; i++) {
            matrix[i][right] = num++;
        }
        right--;

        // 从右到左填充下边
        if (top <= bottom) {
            for (int i = right; i >= left; i--) {
                matrix[bottom][i] = num++;
            }
            bottom--;
        }

        // 从下到上填充左边
        if (left <= right) {
            for (int i = bottom; i >= top; i--) {
                matrix[i][left] = num++;
            }
            left++;
        }
    }

    // 打印螺旋矩阵
    printf("luoxuan juzheng %dx%d:\n", n, n);
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            printf("%3d ", matrix[i][j]);
        }
        printf("\n");
    }
}

int main() {
    int n;
    printf("input how big: ");
    scanf("%d", &n);

    spiralMatrix(n);
    return 0;
}