二项队列介绍及其实现

最新推荐文章于 2022-10-28 01:23:14 发布
最新推荐文章于 2022-10-28 01:23:14 发布
阅读量1.1k 收藏 16
点赞数 5
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/wyn1564464568/article/details/118767133
版权

注：此博客改编自《数据结构与算法分析：C语言描述》中二项队列一节。

1. 1. 1.二项队列的结构

二项队列(Binomial Queue)是一种可以实现：
( 1 ) (1) (1)向其中添加元素；
( 2 ) (2) (2)删除、获取其中的最小(最大)元素；
( 3 ) (3) (3)合并两个二项队列 的数据结构。
和它具有相同功能的有左式堆(左偏树)(Leftist Heap)和斜堆(Skew Heap)。但是它们的所有操作都花费 O ( l o g N ) O(logN) O(logN)时间，而二项队列的插入操作只需常数时间。
不同于左偏树和斜堆，二项队列一般地由具有堆序性质的多棵树构成，即森林。每棵堆序树称为二项树(Binomial Tree),它们具有下图所示的结构：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
下面的每个数字表示图中二项树的高度。记深度为 k k k的二项树为 B k B_k Bk​。在 B 4 B_4 B4​中，考察图中每一层的节点数，可以发现符合二项系数 ( 1 , 4 , 6 , 4 , 1 ) (1,4,6,4,1) (1,4,6,4,1)。一般地，高度为 k k k的的二项树在深度为 d d d处的节点总数是 C d k C_d^k Cdk​。
回到二项队列的结构：设一个二项队列包含 N N N个元素，那么将 N N N表示为它的二进制形式，二项队列便由 p o p c o u n t ( N ) popcount(N) popcount(N)个二项树组成，其中 p o p c o u n t ( N ) popcount(N) popcount(N)表示 N N N的二进制表示中 1 1 1的个数。每个二项树对应一个2的幂：例如，一个二项队列包含 13 13 13个元素，将 13 13 13写为二进制 110 1 ( 2 ) = 8 + 4 + 1 1101_{(2)}=8+4+1 1101(2)​=8+4+1，那么这个二项队列便由深度为 3 、 2 、 0 3、2、0 3、2、0的二项树组成(即 B 3 , B 2 , B 0 B_3,B_2,B_0 B3​,B2​,B0​)。

2. 2. 2.二项队列的操作

2.1 2.1 2.1 求最小(最大)元素

以求最小元素为例。那么，每棵上述的二项树都应该满足小根堆性质。因此，我们可以从所有二项树，最多 l o g N logN logN棵中求得最小元。因此求得最小元的时间复杂度为 O ( l o g N ) O(logN) O(logN)。

2.2 2.2 2.2 合并两个二项队列

由于插入元素可以转化为合并一个二项队列和一个单独的节点，因此我们只需要像左偏树一样解决合并问题即可。
在这里插入图片描述
现在要合并如图所示的两个二项队列 H 1 、 H 2 H_1、H_2 H1​、H2​。合并是通过类似二进制相加的方法完成的：
( 1 ) (1) (1)考察两个二项队列的 B 0 B_0 B0​部分， H 2 H_2 H2​有 B 0 B_0 B0​而 H 1 H_1 H1​没有，因此合成后的二项队列的 B 0 B_0 B0​就是 H 2 H_2 H2​的 B 0 B_0 B0​。
( 2 ) (2) (2)考察 B 1 B_1 B1​部分，两个二项队列均有 B 1 B_1 B1​，比较二者的根值， H 2 H_2 H2​的根值较小，为 14 14 14，因此为了保持小根堆的性质，我们将 H 2 H_2 H2​的 B 1 B_1 B1​加入到 H 1 H_1 H1​的上面，如下图；
( 3 ) (3) (3)考察 B 2 B_2 B2​部分，此时不仅 H 1 , H 2 H_1,H_2 H1​,H2​有 B 2 B_2 B2​，刚才在 ( 2 ) (2) (2)中我们像进位一样得到了一个 B 2 B_2 B2​，因此现在共有三个 B 2 B_2 B2​。将其中两个合并(同样要保持小根堆性质，这里选择除了进位得到的那两个合并)，得到一个 B 3 B_3 B3​,剩下一个(这里选择刚才进位得到的)作为新二项队列的 B 2 B_2 B2​部分。
( 4 ) (4) (4)原先的二项队列没有 B 3 B_3 B3​,但刚才 ( 3 ) (3) (3)中进位得到了一个，将它作为新二项队列的 B 3 B_3 B3​部分。
经过上述过程，两个二项队列合并为一个。
在这里插入图片描述
图中的颜色对应了合并前后各数据的位置。

2.3 2.3 2.3 删除最小(最大)元素

删除最小元素，需要先确定最小元素在哪一棵二项树上，这可以通过 O ( l o g N ) O(logN) O(logN)的遍历确定。然后将这棵二项树的堆顶抹去：
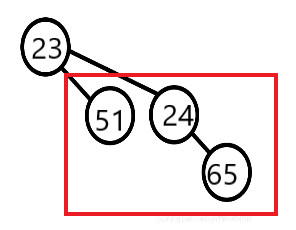
在这里插入图片描述
如图所示，若这个二项树是最小元素所在的二项树，去掉堆顶元素后红框圈起的部分变成了一个 B 1 B_1 B1​，可以视作一个新的二项队列，那么只需要将这个新的二项队列 H ′ ′ H'' H′′与原二项队列除掉这棵二项树得到的 H ′ H' H′合并即可。来看一个例子：
在这里插入图片描述
在刚才合并得到的二项队列中，我们要删除最小元 12 12 12，先找到它所在的二项树 B 3 B_3 B3​:
在这里插入图片描述
去掉 12 12 12，得到一个新的二项队列：
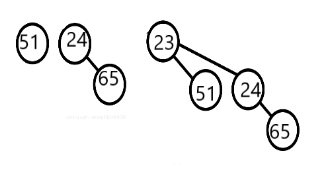
在这里插入图片描述
合并它和剩下的
在这里插入图片描述
即可。合并结果：
在这里插入图片描述
(由于涉及进位，结果不唯一)

3. 3. 3.代码实现

这里采用C++的一些语法。
首先是类型声明：
由于我们在删除操作后需要堆顶元素的儿子节点，所以我们采用链表式的结构：每个节点记录它的第一个儿子节点和下一个兄弟节点，代码如下：

struct BinNode
{
	int Element;//存放数据
	BinNode *FirstChild;//第一个儿子
	BinNode *NextSibling;//下一个兄弟节点
};

在这里插入图片描述

下图是链表式的存法：
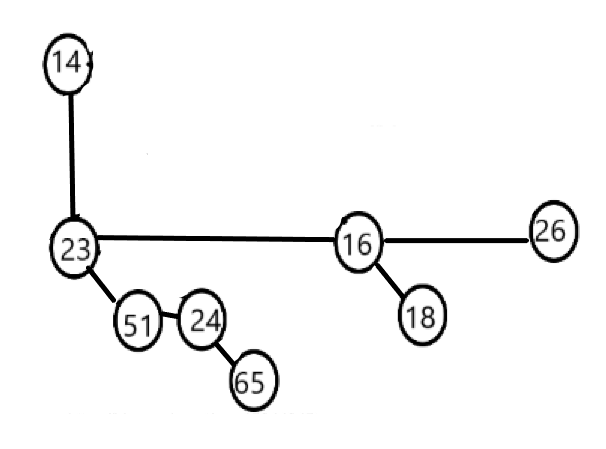
在这里插入图片描述

结构如图所示。横线表示下一个兄弟节点的指针，斜线表示第一个儿子节点指针。图中画的儿子按子树从大到小排列，这样做可以保证在合成两个相同大小的二项树时保持其原有的性质，见下面例子的图解。

再用一个结构体将所有二项树整合起来：

struct BinQueue
{
	int CurrentSize;
	BinNode *Trees[18];
};

C u r r e n t S i z e CurrentSize CurrentSize表示当前二项队列的大小， 18 18 18大小的二项树数组可以存放 1 0 5 10^5 105级别的数据。 ( 2 0 + 2 1 + . . + 2 17 = 262143 > 1 0 5 ) (2^0+2^1+..+2^{17}=262143>10^5) (20+21+..+217=262143>105)

初始化一个空的二项队列的函数：

BinQueue* Initialize()
{
	BinQueue *Init = (BinQueue*)malloc(sizeof(BinQueue));
	Init->CurrentSize = 0;
	for(int i=0;i<MaxTrees;i++)
		Init->Trees[i] = NULL;
	return Init;
}

在合并两个二项队列的时候，我们总是合并两个相同大小的二项树，代码如下：

BinNode* CombineTrees(BinNode *T1,BinNode *T2)
{
	if(T1->Element > T2->Element)
		return CombineTrees(T2,T1);
	T2->NextSibling = T1->FirstChild;
	T1->FirstChild = T2;
	return T1;
}

我们假设 T 1 T_1 T1​的根节点较小，因此当 T 1 T_1 T1​的根节点大时交换两棵二项树。合并时，将 T 1 T_1 T1​的第一个儿子设为 T 2 T_2 T2​的根，同时让 T 2 T_2 T2​的下一个兄弟节点指向原先 T 1 T_1 T1​的儿子节点。
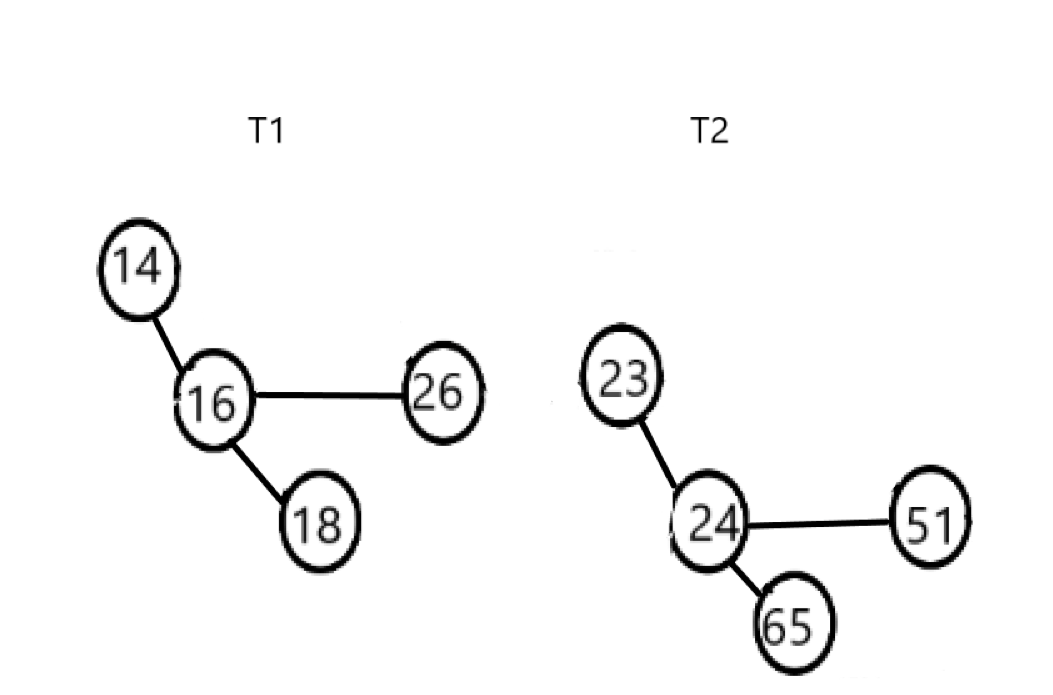
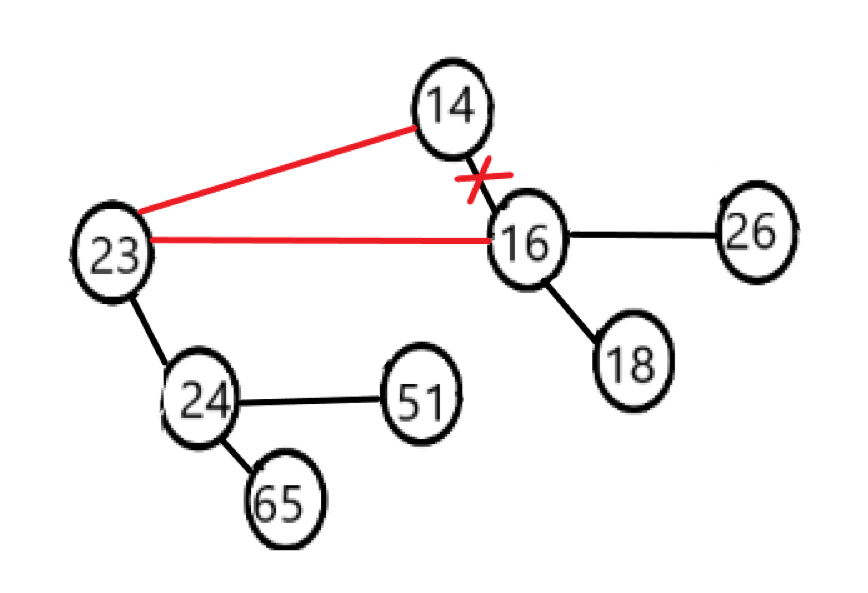
在这里插入图片描述

在这里插入图片描述
在合并过程中，其中根较大的二项树成为了另一个二项树的第一个儿子，这也保持了儿子从大到小排列的性质。

然后是合并的总代码，代码较长，但主要是对是否有空树和进位的 8 8 8种情况的讨论：

BinQueue* Merge(BinQueue *H1,BinQueue *H2)//将H2合并到H1上
{
	BinNode *T1,*T2,*Carry  = NULL;
	int i,j;
	
	H1->CurrentSize += H2->CurrentSize;//更新大小
	for(i = 0,j = 1;j <= H1->CurrentSize;i++,j <<= 1)
	{
		T1 = H1->Trees[i];
		T2 = H2->Trees[i];//两个对应的二项树
		
		switch(!!T1 + 2 * !!T2 + 4 * !!Carry)//见下面的说明
		{
			case 0:
				break;
			case 1:
				break;
			case 2:
				H1->Trees[i] = T2;
				H2->Trees[i] = NULL;
				break;
			case 3:
				Carry = CombineTrees(T1,T2);
				H1->Trees[i] = H2->Trees[i] = NULL;
				break;
			case 4:
				H1->Trees[i] = Carry;
				Carry = NULL;
				break;
			case 5:
				Carry = CombineTrees(T1,Carry);
				H1->Trees[i] = NULL;
				break;
			case 6:
				Carry = CombineTrees(T2,Carry);
				H2->Trees[i] = NULL;
				break;
			case 7:
				H1->Trees[i] = Carry;
				Carry = CombineTrees(T1,T2);
				break;
				
		}
	}
	return H1;
}

switch中的语句是对讨论内容的简写。它基于这样的事实：当 T = = N U L L T == NULL T==NULL， !   T = 1 , ! !   T = 0 !\ T =1,!!\ T = 0 ! T=1,!! T=0；反之，当 T T T不为 N U L L NULL NULL, ! !   T = 1 !!\ T=1 !! T=1。因此switch中的内容是用三个 T 1 , T 2 , C a r r y T_1,T_2,Carry T1​,T2​,Carry(进位)编码的一个二进制数 ( C T 2 T 1 ) ( 2 ) (CT_2T_1)_{(2)} (CT2​T1​)(2)​.
进一步对讨论的内容说明：
case 0 : 000 0:000 0:000，此时三棵树 ( C a r r y , T 1 , T 2 ) (Carry,T_1,T_2) (Carry,T1​,T2​)均为空，跳过；
case 1 : 001 1:001 1:001，此时 T 1 T_1 T1​非空，其他均为空，由于就是要将 T 2 T_2 T2​合并到 T 1 T_1 T1​上，跳过即可。
case 2 : 010 2:010 2:010，此时仅有 T 2 T_2 T2​非空，将它合并到 T 1 T_1 T1​上后设为 N U L L NULL NULL。
case 3 : 011 3:011 3:011，此时 T 1 , T 2 T_1,T_2 T1​,T2​非空，把它们合并后进位。
case 4 : 100 4:100 4:100，此时仅有进位，把进位保留在这一位上，并且设为 N U L L NULL NULL。
case 5 : 101 5:101 5:101，此时进位和 T 1 T_1 T1​非空，把进位和 T 1 T_1 T1​合并作为新的进位。
case 6 : 110 6:110 6:110，与case 5 5 5类似，把进位和 T 2 T_2 T2​合并作为新的进位。
case 7 : 111 7:111 7:111，此时三棵树都非空，这里选择将进位得来的树保留在此位置，剩下两棵树作为新的进位。
最后返回 H 1 H_1 H1​即可。

有了合并的代码，我们可以写出插入的代码：

void Insert(BinQueue *H,int X)
{
	BinQueue *SingleNode = Initialize();
	SingleNode->Trees[0] = (BinNode*)malloc(sizeof(BinNode));
	SingleNode->Trees[0]->Element = X;
	SingleNode->Trees[0]->FirstChild = SingleNode->Trees[0]->NextSibling = NULL;
	SingleNode->CurrentSize = 1;
	Merge(H,SingleNode);
}

最后是删除部分：

int DeleteMin(BinQueue *H)
{
	int i,j;
	int MinTree;
	BinQueue *DeletedQueue;
	BinNode *DeletedTree,*OldRoot;
	int MinItem = INT_MAX;
	for(int i=0;i<MaxTrees;i++)
	{
		if(H->Trees[i] && H->Trees[i]->Element < MinItem)
		{
			MinItem = H->Trees[i]->Element;
			MinTree = i;
		}
	}//找出最小元素所在的二项树
	
	DeletedTree = H->Trees[MinTree];
	OldRoot = DeletedTree;
	DeletedTree = DeletedTree->FirstChild;//指向儿子们
	free(OldRoot);//删掉根节点
	
	DeletedQueue = Initialize();//删除最小元后的新的二项队列H''
	DeletedQueue->CurrentSize = (1<<MinTree)-1;
	//原先这个二项树有2的(MinTree)次方个元素，删掉最小元
	for(j=MinTree-1;j>=0;j--)
	{
		DeletedQueue->Trees[j] = DeletedTree;
		DeletedTree = DeletedTree->NextSibling;
		DeletedQueue->Trees[j]->NextSibling = NULL;
	}//用链表遍历剩下的儿子们，添加到新的H''中
	
	H->Trees[MinTree] = NULL;//除掉最小元所在的二项树
	H->CurrentSize -= DeletedQueue->CurrentSize+1;//更新大小，减去H''的大小再+1(最小元)
	Merge(H,DeletedQueue);//合并即可
	
	return MinItem;
}

实现细节见注释。

例题：洛谷P1456 Monkey King

题目链接

题目大意：

有 N N N只猴子，每只猴子有一个强壮值，每只猴子最开始不认识；给定 M M M次询问，每次询问让两只猴子所在的猴群猴子中最强壮的两个打架，打架后最强壮的两只猴子强壮值除以二(向下取整)，同时两群猴子会互相认识。对于每次询问，输出合并后这群猴子最强壮的那个的强壮值。如果两群猴子一开始就认识，输出 − 1 -1 −1。
注：多组数据。

题解：

显然这是一个可并堆的问题，同时为了维护两个猴子是否互相认识我们需要采用并查集。一开始开 N N N个二项队列维护，按照题意模拟即可。
注意前面的例子都是小根堆，这里要改成大根堆，找最小元和合并两个二项树的时候要注意顺序。在上面例程的基础上还增加了一个获取最大值而不删除的函数。

C o d e : Code: Code:

#include<cstdio>
#include<cstdlib>
#include<climits>

const int MaxTrees = 18;
const int MAXN = 1E5+1;

int fa[MAXN];
int findfa(int x)
{
	return fa[x] == x?fa[x]:fa[x] = findfa(fa[x]);
}
void unity(int x,int y)
{
	fa[findfa(x)] = findfa(y);
}
struct BinNode
{
	int Element;
	BinNode *FirstChild;
	BinNode *NextSibling;
};

struct BinQueue
{
	int CurrentSize;
	BinNode *Trees[18];
};

BinNode* CombineTrees(BinNode *T1,BinNode *T2)
{
	if(T1->Element < T2->Element)
		return CombineTrees(T2,T1);
	T2->NextSibling = T1->FirstChild;
	T1->FirstChild = T2;
	return T1;
}

BinQueue* Merge(BinQueue *H1,BinQueue *H2)
{
	BinNode *T1,*T2,*Carry  = NULL;
	int i,j;
	
	H1->CurrentSize += H2->CurrentSize;
	for(i = 0,j = 1;j <= H1->CurrentSize;i++,j <<= 1)
	{
		T1 = H1->Trees[i];
		T2 = H2->Trees[i];
		
		switch(!!T1 + 2 * !!T2 + 4 * !!Carry)
		{
			case 0:
				break;
			case 1:
				break;
			case 2:
				H1->Trees[i] = T2;
				H2->Trees[i] = NULL;
				break;
			case 3:
				Carry = CombineTrees(T1,T2);
				H1->Trees[i] = H2->Trees[i] = NULL;
				break;
			case 4:
				H1->Trees[i] = Carry;
				Carry = NULL;
				break;
			case 5:
				Carry = CombineTrees(T1,Carry);
				H1->Trees[i] = NULL;
				break;
			case 6:
				Carry = CombineTrees(T2,Carry);
				H2->Trees[i] = NULL;
				break;
			case 7:
				H1->Trees[i] = Carry;
				Carry = CombineTrees(T1,T2);
				break;
				
		}
	}
	return H1;
}

BinQueue* Initialize()
{
	BinQueue *Init = (BinQueue*)malloc(sizeof(BinQueue));
	Init->CurrentSize = 0;
	for(int i=0;i<MaxTrees;i++)
		Init->Trees[i] = NULL;
	return Init;
}

int GetMax(BinQueue *H)
{
	int MaxTree;
	int MaxItem = 0;
	for(int i=0;i<MaxTrees;i++)
	{
		if(H->Trees[i] && H->Trees[i]->Element > MaxItem)
		{
			MaxItem = H->Trees[i]->Element;
			MaxTree = i;
		}
	}
	return MaxItem;
}
int GetMaxId(BinQueue *H)
{
	int MaxTree;
	int MaxItem = 0;
	for(int i=0;i<MaxTrees;i++)
	{
		if(H->Trees[i] && H->Trees[i]->Element > MaxItem)
		{
			MaxItem = H->Trees[i]->Element;
			MaxTree = i;
		}
	}
	return H->Trees[MaxTree]->id;
}
int DeleteMax(BinQueue *H)
{
	int MaxTree;
	BinQueue *DeletedQueue;
	BinNode *DeletedTree,*OldRoot;
	int MaxItem = 0;
	for(int i=0;i<MaxTrees;i++)
	{
		if(H->Trees[i] && H->Trees[i]->Element > MaxItem)
		{
			MaxItem = H->Trees[i]->Element;
			MaxTree = i;
		}
	}
	

	DeletedTree = H->Trees[MaxTree];
	OldRoot = DeletedTree;
	DeletedTree = DeletedTree->FirstChild;

	free(OldRoot);

	DeletedQueue = Initialize();
	DeletedQueue->CurrentSize = (1<<MaxTree)-1;
	for(int j=MaxTree-1;j>=0;j--)
	{
		DeletedQueue->Trees[j] = DeletedTree;
		DeletedTree = DeletedTree->NextSibling;
		DeletedQueue->Trees[j]->NextSibling = NULL;
	}
	
	H->Trees[MaxTree] = NULL;
	H->CurrentSize -= DeletedQueue->CurrentSize+1;
	Merge(H,DeletedQueue);
	
	return MaxItem;
}

void Insert(BinQueue *H,int X)
{
	BinQueue *SingleNode = Initialize();
	SingleNode->Trees[0] = (BinNode*)malloc(sizeof(BinNode));
	SingleNode->Trees[0]->Element = X;
	SingleNode->Trees[0]->FirstChild = SingleNode->Trees[0]->NextSibling = NULL;
	SingleNode->CurrentSize = 1;
	Merge(H,SingleNode);
}
int main()
{
	int n,m,x;
	BinQueue *H[MAXN];
	while(scanf("%d",&n) != EOF)
	{
		for(int i=1;i<=n;i++)
		{
			fa[i] = i;
			H[i] = Initialize();
			scanf("%d",&x);
			Insert(H[i],x);
		}
		scanf("%d",&m);
		for(int i=1;i<=m;i++)
		{
			int x,y;
			scanf("%d%d",&x,&y);
			x = findfa(x);
			y = findfa(y);
			if(x == y)
			{
				printf("-1\n");
				continue;
			}
			int vx = DeleteMax(H[x]) >> 1;
			int vy = DeleteMax(H[y]) >> 1;
			unity(x,y);
			H[x] = Merge(H[x],H[y]);
			Insert(H[x],vx);
			Insert(H[x],vy);
			H[y] = H[x];
			printf("%d\n",GetMax(H[x]));
		}
	}
	return 0;
}
Castria
关注
  • 5
    点赞
  • 踩
  • 16
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
《数据结构与算法分析》二项队列详解
yw8355507的专栏
08-12 786
前言：       补上这篇博客，就补完一半了。 我的github： 我实现的代码全部贴在我的github中，欢迎大家去参观。 https://github.com/YinWenAtBIT 介绍： 定义：      二项队列不同于左式堆和二叉堆等优先队列的实现之处在于，一个二项队列不是一棵堆序的树，而是堆序树的集合，即森林。堆序树中
23 合并多个排序列表 C++思路
zy
04-26 330
分治的思路很好想 也比较好理解 ListNode* mergelist(ListNode *a, ListNode *b){ if(!a)return b; if(!b)return a; if(a -> val < b -> val){ a -> next = mergelist(a -&...
数据结构与算法分析-C++描述 第6章 二项队列ADT（BinomialQueue）
qq_37172182的博客
04-12 360
二项队列（BinomialQueue）： 虽然左式堆和斜堆都以每次操作花费时间有效支持合并、插入和deleteMin，但还有改进的余地，因为我们知道，二叉堆以每次操作花费常数时间支持插入。二项队列支持所有这三种操作，每次操作的最坏运行情况为，而插入操作平均花费常数时间。 二项队列不同于其他优先队列的实现之处在于，一棵二项队列不是一棵堆序的树，而是堆序的树的集合，称...
数据结构--二项队列分析及实现
weixin_33908217的博客
05-07 324
一，介绍 什么是二项队列，为什么会用到二项队列？ 与二叉堆一样，二项队列也是优先级队列的一种实现方式。在 数据结构--堆的实现之深入分析 的末尾 ，简单地比较了一下二叉堆与二项队列。 对于二项队列而言，它可以弥补二叉堆的不足:merge操作的时间复杂度为O(N)。二项队列的merge操作的最坏时间复杂度为O(logN)。 二项队列的合并操作为什么是O(logN)？因为：对于N个结点的二项队...
Binomial Queue
Copy
05-12 388
前面堆排序已经描述了二叉堆的基本操作，插入(O(logn))、删除(O(logn))和查询最大最小值(O(1))，但是两个二叉堆合并时却很不方便，一个一个调用插入方法完成合并需要O(n)。 [b]Binomial Queue[/b](二项队列)：一个链表数组，每个元素指向一棵二项树，数组元素按二项树大小顺序排列。 [b]Binomial Tree(二项树) 是什么 图解[/b] [i...
7-2 Binomial Queue
Jackson_Huuu的博客
10-28 235
Binomial Queue
C++二项队列实现.zip
08-20
在C++中实现二项队列可以帮助我们处理一些需要高效优先级操作的问题。 二项队列的基本概念： 1. 二项队列是由若干个完全二项树（每个节点最多有两个子节点）组成的序列，这些树的根节点按从左到右的顺序排列。 2. ...
数据结构学习--队列及其应用
06-25
数据结构学习--队列及其应用 队列是一种重要的数据结构，它广泛应用于计算机科学和信息技术领域。队列的应用非常广泛，例如医院排队、银行排队、超market排队等等。 一、队列的定义 队列是一种特殊的线性表，它...
普通队列、双端队列的原理详解及其python实现
01-20
文章目录一、原理详解二、python实现（一）、普通队列1、python实现2、代码测试（二）、双端队列1、Python代码实现2、测试代码 一、原理详解 队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的...
栈和队列的基本操作实现及其应用实验报告
12-20
1、熟练掌握栈和队列的基本操作在两种存储结构上的实现。 2、会用栈和队列解决简单的实际问题。 二、实验内容 题目：试写一个算法，判断依次读入的一个以@为结束符的字符序列，是否为回文。所谓“回文“是指正向读...
二项队列的C实现
11-30
二项队列的C实现
基于 C++线性表及其实现 栈和队列及其应用课程实验（实验报告+源码）
06-27
【作品名称】：线性表及其实现 栈和队列及其应用【课程实验】（实验报告+源码） 【适用人群】：适用于希望学习不同技术领域的小白或进阶学习者。可作为毕设项目、课程设计、大作业、工程实训或初期项目立项。 ...
合并k个有序链表
qq_35828475的博客
08-31 192
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode() {} * ListNode(int val) { this.val = val; } * ListNode(int val, ListNode next) { this.val = val; this.next = next; } * }.
优先队列之二项队列(JAVA实现)
MC的博客
06-18 1109
优先队列至二项队列的理解以及JAVA实现
二项队列（类结构及节点定义）
wangjiang1234554321的博客
03-09 567
二项队列的构造函数和常用操作
二项树及二项队列
yanerhao的专栏
12-14 4587
二项树及二项队列
队列的应用——打印二项展开式(a+b)^k的系数（杨辉三角）
qq1169091731的博客
04-09 3656
#include &lt;iostream&gt; using namespace std; #define Max 100 class SeqQueue { public: SeqQueue(); void EnQueue(int x); int DeQueue(); int GetFront(); int GetRear(); bool IsE...
队列---简单实现杨辉三角求二项式的系数值
江城的博客
06-30 1744
队列 队列是另一种限定存取位置的线性表。它只允许在表的一端插入，在另一端删除。允许插入的一端叫做队尾，允许删除的一端叫做队头。 利用数组建立队列 由上图对队列的描述来看，定长的数组很快就会溢出。 但是，这种“溢出”可能是假溢出，因为数组的前端可能还有空位置。为了能够充分的利用数组的存储空间，把数组的前端和和后端连接起来，形成一个环形的表，让队列成为一个循环队列。 循环队列：数组首...
odoo12中国化财务核算解决方案2.30E (1).pdf
最新发布
07-11
odoo12中国化财务核算解决方案2.30E (1)
实现一个循环队列及其基本功能
05-17
循环队列是一种使用循环数组实现的队列。它具有固定大小，当元素填满数组时，它可以覆盖之前的元素。循环队列的基本功能包括入队、出队、判断队列是否为空、判断队列是否已满、获取队首元素、获取队列长度等。 以下是一个简单的循环队列的实现，包括基本功能的实现： ```python class CircularQueue: def __init__(self, k: int): self.queue = [None] * k self.head = 0 self.tail = 0 self.size = 0 self.k = k def enqueue(self, value: int) -> bool: if self.is_full(): return False self.queue[self.tail] = value self.tail = (self.tail + 1) % self.k self.size += 1 return True def dequeue(self) -> bool: if self.is_empty(): return False self.queue[self.head] = None self.head = (self.head + 1) % self.k self.size -= 1 return True def is_empty(self) -> bool: return self.size == 0 def is_full(self) -> bool: return self.size == self.k def get_front(self) -> int: if self.is_empty(): return -1 return self.queue[self.head] def get_rear(self) -> int: if self.is_empty(): return -1 return self.queue[self.tail - 1] def get_size(self) -> int: return self.size ``` 在上面的代码中，我们使用了一个长度为 k 的列表来实现循环队列。通过维护头部指针 head 和尾部指针 tail，我们可以确定队列的位置。我们还使用 size 来跟踪队列中的元素数量。enqueue 和 dequeue 操作分别向队列中添加和移除元素，并且它们都可以在 O(1) 的时间内完成。其他操作也都可以在 O(1) 时间内完成。 使用示例： ```python # 创建一个长度为 3 的循环队列 cq = CircularQueue(3) # 入队 cq.enqueue(1) cq.enqueue(2) cq.enqueue(3) # 获取队列长度 assert cq.get_size() == 3 # 判断队列是否已满 assert cq.is_full() == True # 尝试入队，但队列已满，返回 False assert cq.enqueue(4) == False # 出队 cq.dequeue() # 获取队首元素 assert cq.get_front() == 2 # 获取队尾元素 assert cq.get_rear() == 3 # 判断队列是否为空 assert cq.is_empty() == False # 全部出队 cq.dequeue() cq.dequeue() # 判断队列是否为空 assert cq.is_empty() == True ```

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值