方法:多项式求ln
解析:
毒瘤题的倒数第二个- -!
md毒瘤题都做完后再回来写题解真是爽歪歪
先看这道题怎么做。
首先一个简单无向图的边的个数是C(n,2),然后那么我们的选择就有
2C(n,2)
种。
然后我们再考虑简单无向连通图的方案数为fi。
f[i]=2C(i,2)−∑i−1j=1f[j]∗C(i−1,j−1)∗2C(i−j,2)
上面的式子其实没啥卵用…
现在我们这么来考虑。

看如上大爷给出的PPT。
其实这个正体现了划分和被划分的关系。
对于简单无向图来说,简单无向连通图就是简单无向图的一个划分。
所以搞出来简单无向图的指数级生成函数。
G(x)=∑∞i=02C(i,2)∗xii!
然后再搞出来简单无向连通图的指数级生成函数。
F(x)=∑∞i=0fi∗xii!
于是有
G(x)=eF(x)
故
F(x)=ln(G(x))
简单求个ln即可辣。
ln怎么求呢?
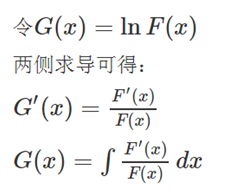
求导O(n),积分O(n)。
求逆O(nlogn)
总复杂度T(n)=T(n/2)+O(nlogn)=O(nlogn)
代码:
using namespace std;
typedef long long ll;
int n;
ll Factor[N],Inv_Fac[N];
ll G[N],inv_G[N],dao_G[N];
int rev[N];
ll Quick_Power(ll x,ll y,ll MOD)
{
ll ret=1;
while(y)
{
if(y&1)ret=(ret*x)%MOD;
x=(x*x)%MOD;
y>>=1;
}
return ret;
}
void init()
{
Factor[0]=1,Inv_Fac[0]=1;
for(int i=1;i<=n;i++)
{
Factor[i]=Factor[i-1]*i%mod;
Inv_Fac[i]=Quick_Power(Factor[i],mod-2,mod);
}
}
void NTT(ll *a,int n,int f)
{
for(int i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
for(int h=2;h<=n;h<<=1)
{
ll wn=Quick_Power(3,(mod-1)/h,mod);
for(int i=0;i<n;i+=h)
{
ll w=1;
for(int j=0;j<(h>>1);j++,w=w*wn%mod)
{
ll t=a[i+j+(h>>1)]*w%mod;
a[i+j+(h>>1)]=((a[i+j]-t)%mod+mod)%mod;
a[i+j]=(a[i+j]+t)%mod;
}
}
}
if(f==-1)
{
for(int i=1;i<(n>>1);i++)swap(a[i],a[n-i]);
ll inv=Quick_Power(n,mod-2,mod);
for(int i=0;i<n;i++)a[i]=a[i]*inv%mod;
}
}
void Get_Inv(ll *a,ll *b,int n)
{
static ll temp[N];
if(n==1)
{
b[0]=Quick_Power(a[0],mod-2,mod);
return ;
}
Get_Inv(a,b,n>>1);
memcpy(temp,a,sizeof(a[0])*n);
memset(temp+n,0,sizeof(a[0])*n);
int m=n,L=0,nn=n;
for(n=1;n<=m;n<<=1)L++;
for(int i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
NTT(temp,n,1),NTT(b,n,1);
for(int i=0;i<n;i++)
temp[i]=b[i]*(((2ll-temp[i]*b[i]%mod)%mod+mod)%mod)%mod;
NTT(temp,n,-1);
for(int i=0;i<(n>>1);i++)b[i]=temp[i];
memset(b+nn,0,sizeof(b[0])*nn);
n=nn;
}
int main()
{
scanf("%d",&n);
init();
for(int i=0;i<=n;i++)
{
if(i<2)G[i]=1;
else G[i]=Quick_Power(2,(long long)i*(i-1)/2,mod)*Inv_Fac[i]%mod;
}
for(int i=1;i<=n;i++)
{
dao_G[i-1]=G[i]*i%mod;
}
dao_G[n]=0;
int l;
for(l=1;l<=n;l<<=1);
Get_Inv(G,inv_G,l);
int m=n,L=0;
for(n=1;n<=m;n<<=1)L++;
for(int i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
NTT(dao_G,n,1),NTT(inv_G,n,1);
for(int i=0;i<n;i++)
dao_G[i]=(inv_G[i]*dao_G[i])%mod;
NTT(dao_G,n,-1);
printf("%lld\n",(dao_G[m-1]*Quick_Power(m,mod-2,mod)%mod)*Factor[m]%mod);
}










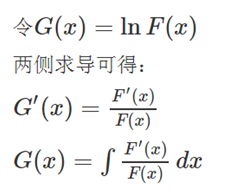














 106
106

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








