字符串全排列算法

前言

字符串的排列组合问题，困扰了我好久，递归的思想我今天一定要掌握，擦，话不多说，博客走起！

问题

输入一个字符串，打印出该字符串中字符的所有排列。例如输入字符串abc，则输出由字符a，b，c所能排列出来的所有字符串abc，acb，bac，bca，cab和cba

思路

这是典型的递归求解问题，递归算法有四个特性：

• 必须有可达到的终止条件，否则程序陷入死循环
• 子问题在规模上比原问题小
• 子问题可通过再次递归调用求解
• 子问题的解应能组合成整个问题的解

对于字符串的排列问题：

如果能生成n-1个元素的全排列，就能生成n个元素的全排列。对于只有一个元素的集合，可以直接生成全排列。所以全排列的递归终止条件很明确，只有一个元素时。我们可以分析一下全排列的过程：

1. 首先，我们固定第一个字符a，求后面两个字符bc的排列
2. 当两个字符bc排列求好之后，我们把第一个字符a和后面的b交换，得到bac，接着我们固定第一个字符b，求后面两个字符ac的排列
3. 现在是把c放在第一个位置的时候了，但是记住前面我们已经把原先的第一个字符a和后面的b做了交换，为了保证这次c仍是和原先处在第一个位置的a交换，我们在拿c和第一个字符交换之前，先要把b和a交换回来。在交换b和a之后，再拿c和处于第一位置的a进行交换，得到cba。我们再次固定第一个字符c，求后面两个字符b、a的排列
4. 既然我们已经知道怎么求三个字符的排列，那么固定第一个字符之后求后面两个字符的排列，就是典型的递归思路了

下面这张图很清楚的给出了递归的过程：

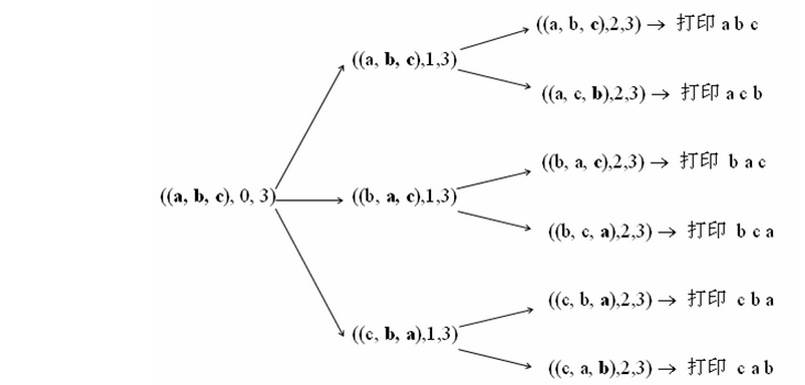
示例题目

题目描述

题目描述：
给定一个由不同的小写字母组成的字符串，输出这个字符串的所有全排列。
我们假设对于小写字母有'a' < 'b' < ... < 'y' < 'z'，而且给定的字符串中的字母已经按照从小到大的顺序排列。
输入：
输入只有一行，是一个由不同的小写字母组成的字符串，已知字符串的长度在1到6之间。
输出：
输出这个字符串的所有排列方式，每行一个排列。要求字母序比较小的排列在前面。字母序如下定义：
已知S = s1s2...sk , T = t1t2...tk，则S < T 等价于，存在p (1 <= p <= k)，使得
s1 = t1, s2 = t2, ..., sp - 1 = tp - 1, sp < tp成立。
样例输入：
abc
样例输出：
abc
acb
bac
bca
cab
cba
提示：
每组样例输出结束后要再输出一个回车。

ac代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
 
struct seq
{
    char str[7];
};
 
struct seq seqs[721];
int count;
 
void swap(char *str, int a, int b)
{
    char temp;
    temp = str[a];
    str[a] = str[b];
    str[b] = temp;
}
 
void permutation_process(char *name, int begin, int end) {
    int k;
 
    if (begin == end - 1) {
        strcpy(seqs[count].str, name);
        count ++;
    }else {
        for (k = begin; k < end; k ++) {
            swap(name, k, begin);
            permutation_process(name, begin + 1, end);
            swap(name, k, begin);
        }
    }
}
 
int compare(const void *p, const void *q)
{
    const char *a = p;
    const char *b = q;
    return strcmp(a, b);
}
 
int main()
{
    char name[7];
    int i, len;
 
    while (scanf("%s", name) != EOF) {
        count = 0;
        len = strlen(name);
        permutation_process(name, 0, len);
        qsort(seqs, count, sizeof(seqs[0]), compare);
 
        for (i = 0; i < count; i ++) {
            printf("%s\n", seqs[i].str);
        }
        printf("\n");
    }
 
    return 0;
}
 
/**************************************************************
    Problem: 1120
    User: wangzhengyi
    Language: C
    Result: Accepted
    Time:710 ms
    Memory:920 kb
****************************************************************/

去掉重复的全排列

上述代码有个缺陷，就是会造成重复数据的输出，例如abb这种字符串，上述程序跑完结果如图：

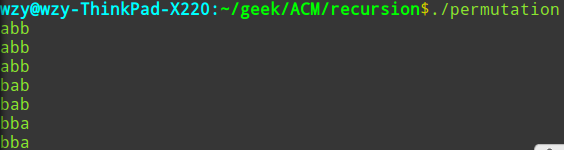
由于全排列就是从第一个数字起，每个数分别与它后面的数字交换，我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这两个数就不交换了。例如abb，第一个数与后面两个数交换得bab，bba。然后abb中第二个数和第三个数相同，就不用交换了。但是对bab，第二个数和第三个数不同，则需要交换，得到bba。由于这里的bba和开始第一个数与第三个数交换的结果相同了，因此这个方法不行。

换种思维，对abb，第一个数a与第二个数b交换得到bab，然后考虑第一个数与第三个数交换，此时由于第三个数等于第二个数，所以第一个数就不再用与第三个数交换了。再考虑bab，它的第二个数与第三个数交换可以解决bba。此时全排列生成完毕！

这样，我们得到在全排列中去掉重复的规则：

去重的全排列就是从第一个数字起，每个数分别与它后面非重复出现的数字交换。

贴出上面ac代码的去重版本：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

struct seq
{
	char str[7];
};

struct seq seqs[721];
int count;

int is_swap(char *str, int begin, int k)
{
	int i, flag;

	for (i = begin, flag = 1; i < k; i ++) {
		if (str[i] == str[k]) {
			flag = 0;
			break;
		}
	}

	return flag;
}

void swap(char *str, int a, int b)
{
	char temp;
	temp = str[a];
	str[a] = str[b];
	str[b] = temp;
}

void permutation_process(char *name, int begin, int end) {
	int k;

	if (begin == end - 1) {
		strcpy(seqs[count].str, name);
		count ++;
	}else {
		for (k = begin; k < end; k ++) {
			if (is_swap(name, begin, k)) {
				swap(name, k, begin);
				permutation_process(name, begin + 1, end);
				swap(name, k, begin);
			}
		}
	}
}

int compare(const void *p, const void *q)
{
	const char *a = p;
	const char *b = q;
	return strcmp(a, b);
}

int main()
{
	char name[7];
	int i, len;

	while (scanf("%s", name) != EOF) {
		count = 0;
		len = strlen(name);
		permutation_process(name, 0, len);
		qsort(seqs, count, sizeof(seqs[0]), compare);

		for (i = 0; i < count; i ++) {
			printf("%s\n", seqs[i].str);
		}
		printf("\n");
	}

	return 0;
}

参考链接

• http://blog.csdn.net/wuzhekai1985/article/details/6643127
• http://blog.csdn.net/hackbuteer1/article/details/7462447