前言
今天本来应该看《信息检索导论》的,但是早上在九度oj做题目的时候碰到一个很有意思的题目,需要用到三分搜索算法。大家都知道二分搜索算法作为分治中最常见的方法,适用于单调函数,逼近求解某点的值。但当函数具有凹凸性时,二分搜索就无法使用了(当然可以先排序),这里介绍一种新的方法,三分查找算法,适应的函数图形如下:
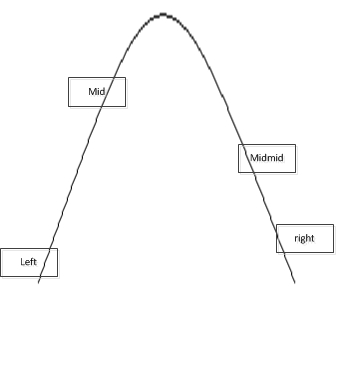
算法思想
1. 与二分查找算法类似,先取整个区间的中间值mid
mid = (left + right) / 2;2. 再去右侧区间的中间值midmid,从而把区间分成三个小区间
midmid = (mid + right) / 2;3. 如果mid比midmid更靠近最值点,我们就舍弃右区间(midmid + 1 ~ end),否则我们就舍弃左区间(left ~ mid - 1).
比较mid与midmid谁更靠近最值,只需要确定mid所在的函数值与midmid所在的函数值的大小。当最值为最大值时,mid与midmid中较大的那个自然更为靠近最值。最值为最小值时同理
if (cal(mid) < cal(midmid))
left = mid;
else
right = midmid;
4. 重复1,2,3,直到找到最值点
示例
寻找峰值点
题目描述:
给定一个整数序列,该整数序列存在着这几种可能:先递增后递减、先递减后递增、全递减、全递增。
请找出那个最大值的点。
输入:
输入的第一行包括一个整数N(1<=N<=10000)。
接下来的一行是N个满足题目描述条件的整数。
输出:
可能有多组测试数据,对于每组数据,
输出这N个数中最大的那个数。
样例输入:
5
1 2 3 2 1
样例输出:
3ac代码
#include <stdio.h>
#include <stdlib.h>
/**
* 三分搜索
*/
int find_max_num(int *arr, int begin, int end)
{
int mid, midmid, max;
/*mid靠近极值点,舍弃最右部分,midmid靠近极值点,舍弃最左部分*/
while (begin < end) {
if (begin + 1 == end) {
max = arr[begin] > arr[end] ? arr[begin] : arr[end];
return max;
}
mid = (begin + end) / 2;
if (mid + 1 == end) {
midmid = (mid + end) / 2 + 1;
} else {
midmid = (mid + end) / 2;
}
if (midmid == end) {
max = arr[begin] > arr[mid] ? arr[begin] : arr[mid];
max = max > arr[end] ? max : arr[end];
return max;
}
if (arr[mid] >= arr[midmid])
end = midmid;
else
begin = mid;
}
return arr[mid];
}
int main(void)
{
int i, n, max, *arr;
while (scanf("%d", &n) != EOF) {
arr = (int *)malloc(sizeof(int) * n);
for (i = 0; i < n; i ++)
scanf("%d", arr + i);
if (n == 1) {
printf("%d\n", arr[0]);
} else {
max = find_max_num(arr, 0, n - 1);
printf("%d\n", max);
}
free(arr);
}
return 0;
}
/**************************************************************
Problem: 1261
User: wangzhengyi
Language: C
Result: Accepted
Time:540 ms
Memory:912 kb
****************************************************************/



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








