字符串用法、算法总结

时隔多年，我又来写总结啦！！！

update: 2023.9.26

update: 2024.2.1

先总述一下
字符串（string）是一种常用的数据结构，存储方式类似于数组，c++里规定其存储的起始下标为0，通常用$len=s.size()$来表示字符串长度。

另外，字符串也可以char数组的方式实现。此时需用len=strlen(s)求其长度

用法

c++中，string自带的用法有很多，此处仅介绍几个较为初级的、常用的用法。
（注：char数组没有以下用法）

插入

string支持最基础的+=插入。

string s="abcd";
char ch='e';
s+=ch;
//此时s="abcde"

下面列举$insert()$函数的具体用法

string s="abcd",ch="wxyz";
s.insert(2,ch);//在字符串s的位置2上插入字符串ch，此时s="abwxyzcd"
s.insert(2,ch,1,3);//在字符串s的2的位置上插入字符串ch中以位置1为开头，长度为3的字符串，此时s="abxyzcd"
char ch1='x';
s.insert(2,3,ch1);//在字符串s的位置2上插入3个字符ch1，此时s="abxxxcd"

感谢大佬纠错！！！@liang_2026

删除

string s="abcdefg";
s.erase(2,4);//删除字符串s的以位置2为开头、长度为4的子串，此时s="abg"

替换

string s="abcdefg",ch="xyz";
s.replace(2,4,ch);//将字符串s的以位置2为开头，长度为4的子串换成字符串ch，此时s="abxyzg"

用法到此结束。

算法

Hash

引入hash

hash表，又称散列表，一般由hash函数和链表结构共同实现。

hash算法的本质是建立映射关系，其他类似的算法还有离散化和$map（数据结构）$。hash的思想是取一个$p$值，将数字$x$存在$head$数组中$x\mathrm{mod}p$的格子里。但是这显然会有冲突（既必定存在多个$x$，使得$x\mathrm{mod}p$的值相等）。处理这种冲突的最常用方法为拉链法——开一个链表结构（类似于图论中的链式前向星）。具体写法见code：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int a[maxn],head[maxn]/*存储的格子*/;
int A/*数组长度*/,p/*为了达到效果，p要选大于A的质数*/,tot=0;
struct star {//链式前向星
	int nxt,val;
};
star h[maxn];
bool check(int x) {//找质数
	if(x==1) return 0;
	if(x==2) return 1;
	if(x%2==0) return 0;
	for(int j=3;j<=sqrt(x);j+=2)
		if(x%j==0) return 0;
	return 1;
}
void add(int x) {
	int k=(x%p+p)%p;//数字x的hash值，这么写是为了避免x<0的情况
	h[++tot].val=x;//数字原来的值
	h[tot].nxt=head[k];//数字在格子里的位置
	head[k]=tot;//这个格子最后一次存入数字是在第tot个前向星中
}
bool Find(int x) {//查找数字x是否出现过
	for(int j=head[x%p];j!=-1;j=h[j].nxt)
		if(h[j].val==x) return 1;//出现过
	return 0;
}
int main() {
	scanf("%d",&A);
	for(int i=1;i<=A;i++)
		scanf("%d",&a[i]);
	memset(head,-1,sizeof(head));
	for(p=A+1;;p++)
		if(check(p)) break;
	for(int i=1;i<=A;i++)
		add(a[i]);//插入
	return 0;
}

hash算法优于离散化和map的地方在于它的时间复杂度是严格O(n)的。在忽略常数的情况下

字符串hash

普通的hash算法针对的是数字，无法存储字符串。这个算法就是针对字符串而出现的。

对于一个字符串$s$，它的hash值求法是：将$s$中的每个字符都转换成一个数字，然后选取一个数$base$为进制数，将$s$转换位一个$base$进制数的数字。为了方便，我们一般将字符对应的ASCLL码作为其转换的数字，进制数一般取131（因为小写字母z的ASCLL码是所有大小写字母中最大的，为126）。因为这个数字过大，所以我们要进行取模运算。又因为取模运算常数很大，所以我们引入一个unsigned long long（无符号64位整型，范围0~2⁶⁴-1）。当数字大于$0\sim$ 2⁶⁴ $-1$时，它会自动对2⁶⁴取模，而且常数很小（可以想象成位运算）。

所以，一般查找这个字符串有没有出现过时，仅靠字符串hash是不够的，需要搭配数字hash共同实现。code如下：

#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int maxn=50050;
int mod=50021;
struct Hash {//数字hash（见上文）
	int nxt;
	ull val;
};
Hash edge[maxn];
int p=131,n;
int head[maxn],tot=0;
ull Get(string s) {//字符串hash值
	ull num=0;
	for(int j=0;j<s.size();j++)
		num=num*p+(ull)(s[j]-'a'+1);//转换为p进制数
	return num;
}
int H(ull x) {
	return (x%mod+mod)%mod;
}
bool add(ull x) {
	int k=H(x);
	for(int j=head[k];j!=-1;j=edge[j].nxt)
		if(edge[j].val==x) return 1;//出现过
	edge[++tot].val=x;//未出现，插入
	edge[tot].nxt=head[k];
	head[k]=tot;
	return 0;
}
int main() {
	scanf("%d",&n);
	memset(head,-1,sizeof(head));
	for(int i=1;i<=n;i++) {
		string x;
		cin>>x;
		ull res=Get(x);//得出字符串x的hash值
		if(add(res)/*查找res这个数字有没有出现过，如果没有就插入*/) 
			printf("%d\n",i);
	}
	return 0;
}

现在最基础的字符串hash我们已经了解。通过字符串hash我们还可完成更多操作。我们先引入几个公式：

H(S)：字符串S的hash值
H(S+T)=H(S)*p^length(T)+H(T)
H(T)=H(S+T)-H(S)*p^length(T)

通过这三个公式，我们即可在O(n)的时间复杂度内求出字符串S的hash值，并在O(1)的时间复杂度内求出S的任意子串的hash值。例题：兔子与兔子
code：

#include<bits/stdc++.h>
using namespace std;
string s;
const int maxn=1e6+10;
typedef unsigned long long ull;
ull f[maxn],q[maxn];
int p=131;
void Prepare() {
	for(int i=0;i<s.size();i++) {
		if(i==0) f[i+1]=(ull)(s[i]-'a'+1);
		else f[i+1]=f[i]*p+(ull)(s[i]-'a'+1);
		if(i==0) q[i]=1;
		else q[i]=q[i-1]*p;
	}
}
int main() {
	cin>>s;
	Prepare();//O(n)求s各个位置的hash值
	int m;
	scanf("%d",&m);
	for(int i=1;i<=m;i++) {
		int l1,l2,r1,r2;
		scanf("%d%d%d%d",&l1,&l2,&r1,&r2);
		//判断区间[l1,l2]与[r1,r2]是否相等
		ull h1=f[l2]-f[l1-1]*q[l2-l1+1];
		ull h2=f[r2]-f[r1-1]*q[r2-r1+1];
		if(h1==h2) puts("Yes");
		else puts("No");
	}
	return 0;
}

KMP模式匹配

我们先来想一道题目：给定两个串A，B（保证$A.size()<=B.size()$），求A串在B串中出现的次数以及每次出现的位置。

通过我们之前学过的知识，我们便可以解决掉这道题——字符串Hash。部分code如下：

Prepare();//求A，B两个串每个位置的Hash值
int m=A.size(),ans=0;
for(int i=m;i<=B.size();i++)
	if((f_B[i]-f_B[i-m]*p[m])==f_A/*整个A串的Hash值*/) {
		ans++;
		printf("%d\n",i-m+1);//出现的位置
	}
printf("%d",ans);

它的时间复杂度是O(n+m)的。而我们接下来要讲的KMP，它的时间复杂度也是O(n+m)的。那它是不是没什么用呢？？

KMP算法相比于Hash，最大的优点是它不光可以让我们求得A串在B串中出现的次数，还可以告诉我们一些其他的、有用的信息。 我们在后面会详细讲述。
下面开始正式讲述KMP模式匹配算法。

KMP算法的核心在于两个数组：$next$和$f$。$next[i]$表示A串以i为结尾的非前缀子串与A串的前缀子串相等的最大长度。 如果难以理解，请见下方的例子：

A=abababac
next[1]=0;//没有以1为结尾的非前缀子串
next[2]=0;//A[2]!=A[1](以2为结尾的非前缀子串只有A[2])
next[3]=1;//A[3]:a
next[4]=2;//A[3~4]:ab
next[5]=3;//A[3~5]:aba
next[6]=4;//A[3~6]:abab
next[7]=5;//A[3~7]:ababa
next[8]=0;//无

$f[i]$表示B串以i为结尾的子串与A串的前缀子串相等的最大长度。 如果难以理解，请见下方的例子：

A=abac,B=abcabacbabcbab
f[1]=1;
f[2]=2;
f[3]=0;
f[4]=1;
f[5]=2;
f[6]=3;
f[7]=4;//A[1~4]=B[4~7]
......

通过这个例子我们可以发现，当$f[i]==A.size()$的时候，说明此时已经在B串中找到了一个子串，使他等于A串。所以我们最后在统计答案时，就是

if(f[i]==A.size()) {
	ans++;
	printf("%d\n",i-A.size()+1);
}

现在，我们了解了$next$,$f$数组，接下来我们就来探讨next、f数组的求法。

$next$数组的求法

在讲述之前，我们先来引进一个概念：候选项。什么是候选项呢？我们来看一个例子：

A=abababab
next[3]=1;//a
next[5]=3;//aba
next[7]=5;//ababa

通过$next$数组的定义，我们可知，$next[i]$存储的是$A$串以$i$为结尾的非前缀子串与$A$串的前缀子串相等的最大长度，但是，通过上面的例子可知，子串$aba$，$a$也可以满足以上（除最大长度以外的）条件。我们把类似子串对应的next值（既上述例子中的next[5],next[3]） 称为$next[i]$（既上述例子中的$next[7]$）的候选项。

了解了候选项的定义，我们就来深入探讨一下候选项的作用。

现在，让我们再引入一个引理：对于next[i]，如果存在j0是next[i]的一个候选项，那么小于j0的最大的next[i]的候选项是next[j0]。比如上述例子中，3（既$next[5]$）是$next[7]$的候选项，那么，小于3的$next[7]$的最大候选项是$next[3]$（既1）。在此不作证明因为怕读者不懂，请读者自行思考或查阅《算法进阶》等资料。

那么，有了这个引理，当我们求出了$next[i-1]$后，我们便可得知$next[i-1]$的所有候选项：$next[i-1],next[next[i-1]],next[next[next[i-1]]],......$所以，我们的$next[i]$的值就在$next[i-1]+1,next[next[i-1]]+1,next[next[next[i-1]]]+1,......,0$之间。具体见code：

nxt[1]=0;
int j=0/*对于next[i],j表示next[i-1]*/,m=s2.size();
for(int i=2;i<=m;i++) {
	while(j>0 && s2[i-1]!=s2[j]/*当前候选项不符合要求*/) j=nxt[j];//查找下一候选项
	if(s2[i-1]==s2[j]) j++;//此候选项符合标准
	nxt[i]=j;
}

$f$数组的求法

由于定义相似，$f$数组求法再次不多做赘述，具体见code：

int j=0,n=s1.size();
int ans=0;
for(int i=1;i<=n;i++) {
	while(j>0 && (j==m || s1[i-1]!=s2[j])/*这一候选项不符合要求*/) j=nxt[j];
	if(s1[i-1]==s2[j]) j++;
	f[i]=j;
	if(f[i]==m) ans++;//统计答案
}

数组的额外用法

对于$next$数组而言，他还有一个很好的用法：查找该字符串的最短循环元。详情请见题目：Period以及《算法进阶》上的相关内容。

//该code是针对上文例题的,对于其他另有要求的题目，可以不用特判i/(i-nxt[i])>1
for(int i=2;i<=n;i++) {//因为周期次数要大于1，所以必须从2开始
	if(i%(i-nxt[i])==0 && i/(i-nxt[i])>1)//mark
		printf("%d %d\n",i,i/(i-nxt[i]));
}
/*
mark处解释：
由定义可知，nxt[i]表示以i为结尾的非前缀子串与前缀子串相同的最大长度，
那么i-nxt[i]的值就一定是i的所有候选项中(i-nxt[nxt[i]],i-nxt[nxt[nxt[i]]],...)最小的,
现在可证，如果i-nxt[i]是i的因数(既i可以整除(i-nxt[i]))，那么i-nxt[i]也一定是i的候选项，并且一定存在最小的，长度为nxt[i]的循环元
所以如果i%(i-nxt[i])==0,那么就说明已经找到了一个循环元，现在只需判断这个循环元循环的周期是不是1(既这个循环元是不是字符串本身)
*/

最小表示法

定义

我们先来看一组字符串：

S=cdba;
S1=acdb;
S2=bacd;
S3=dbac;
S4=cdba;

不难发现，我们每次将字符串$S$的最后一个字符移到开头，这样循环多次后，就可以得到上述字符串（既$S1$,$S2$,$S3$,$S4$）。我们称这四个字符串是循环同构的。其中，字符串$S1$（既$acdb$）是这四个字符串中字典序最小的，我们就称字符串$S1$是字符串$S$的最小表示。为了方便，我们通常用$B[i]$来表示以位置i为开头的循环同构串。已上述字符串为例，则：$B[1]=S4$,$B[2]=S3$,$B[3]=S2$,$B[4]=S1$。

通俗来讲，最小表示法既为：将字符串$S$循环同构，得到$S.size()$个字符串，其中字典序最小的一个就是$S$的最小表示。

求法

了解了什么是最小表示，接下来就该求字符串的最小表示了。

一般情况下，我们最先想到的方法就是暴力了。既：求出$S$的所有循环同构串，然后$O(n^2)$去比较。实际上，我们可以通过双指针的思路在线性的时间内求出最小表示。

首先，我们将$S$串复制一份补在$S$串后面，得到字符串$SS$。

S=acbd;
SS=acbdacbd;

此时我们来仔细研究下$B[i]$和$B[j]$两个字符串的比较过程。

我们不难发现：$B[i]$和$B[j]$前三位字符均相等，但在比较到第四位字符时，$B[i]$要大于$B[j]$，那么，不难得到结论：$B[i],B[i+1],B[i+2]\dots \dots B[i+k]$都是小于$B[j],B[j+1],B[j+2]\dots \dots B[j+k]$的。那么，$B[i],B[i+1],B[i+2]\dots \dots B[i+k]$就不可能成为最终的答案了，我们可直接让$i=i+k+1$，跳过这一段。但因为$B[j]$还有可能成为最终的答案，所以$j$不做变动。当然，$i$，$j$反过来也一样。但是，我们要注意一点：当$j=i+k+1$时，我们需要让$i++$。因为如果当$i==j$时，继续比下去就没有双指针的作用了。

最后，当$i$或$j$已经延伸了$S.size()$个位置，或者已经大于$S.size()$时，说明最小表示就在$B[min(i,j)]$中。不理解可以查阅《算法进阶》。我才不会说是因为我懒

int i=1,j=2;
while(i<=n && j<=n) {
	int k;
	for(k=0;k<n && s1[i+k]==s1[j+k];k++) ;//注意，此处为空语句
	if(k==n) break;
	if(s1[i+k]>s1[j+k]) {
		i=i+k+1;
		if(i==j) i++;
	}
	else {
		j=j+k+1;
		if(i==j) j++;
	}
}
i=min(i,j);
for(int k=1;k<=n;k++)
	mark1[k]=s1[i+k-1];//mark数组便为最小表示

trie树

定义

trie树是一种字典树，用于实现字符串快速检索的数据结构。trie树的总体结构见下图：

当我们在插入一个字符串到trie树里时，要让连接两个点的有向边来存储字符，在最后一个节点上做标记，表示这个字符串结束。

实现

通常，我们选择用一个二维数组来表示$trie$树，用$tot$表示当前的总结点数。同时，要有一个$end$数组来标记字符串是否结束。

初始化

因为$trie$树本身就具有一个根节点，所以$tot$的初值为1，$trie,end$数组初始均为0。要特别注意的一点就是trie 数组以及end数组开的范围。

int trie[maxn][26], tot = 1;//在这里的26是默认只有大写字母或只有小写字母，要根据不同要求及时变化。
bool ed[maxn];//maxn的数值为总的字符数。例如，一道题中有n个字符串，每个字符串长度不超过m，那么maxn就应该开到n * m。

其中，$trie[i][j]=k$表示第$i$个节点通过边$j$连接到的节点为$k$。

插入

对于插入这个操作，我们可以变相地理解一下：假设这棵树上有着所有字符所对应的边，但是都未被激活。把插入字符串理解为激活字符串。 将$tot$理解为已被激活的字符个数。这时，我们的插入操作（假设插入字符串$cat$）就分为以下几步：

1. 定义一个节点$p$,初始时$p$为根。将$p$通过字符边$c$指向节点$q$。若$q$已被激活，令$p=q$,否则将$q$激活，令$p=q$。
2. 重复上述步骤直至字符串结束，此时将节点$p$所在的节点标记，表明到此有一条完整的字符串。详情见代码：

void add(string x) {
	int p = 1;//新建节点p
	for(int i = 0; i < x.size(); i++) {
		if(trie[p][x[i]-'A'] == 0) trie[p][x[i]-'A'] = ++tot;//节点q未被激活，将其激活
		p = trie[p][x[i]-'A'];//令p = q
	}
	ed[p] = 1;//将节点p标记
	return ;
}

查询

同插入，查询的步骤与插入几乎一致。

1. 新建一个节点$p$，初始时节点$p$为根，将$p$通过字符边$c$指向节点$q$。若$q$未被激活，返回$false$，否则令$p=q$。
2. 重复上述步骤直至字符串查询结束，判断$ed[p]$是否被标记。若未被标记，返回$false$，否则返回$true$。详情见代码：

bool Search(string x) {
	int p = 1;
	for(int i = 0; i < x.size(); i++) {
		int ch = x[i] - 'a';
		int k = trie[p][ch];
		if(!k) return false;//判断q是否被激活
		p = k;
	}
	if(!ed[p]) return false;//判断是否是完整的字符串
	return true;
}

01trie

$trie$树有一个十分有用的算法：01trie，即$trie$树的每一条边存储的是二进制中的$0$或$1$。具体怎么用呢？？我们来看一道例题。
例题：最长异或路径
在这之前，我们先来想一个问题：现在给出$n$个数，让你从中选出两个，使其异或值最大。怎么做呢？？

我们可以将这$n$个数转换为n个长度为$32$的二进制$01$串，然后枚举每一个$01$串。对于某个$01$串的某一位，我们尽可能的去找与其相反的一位。即：如果这一位是$1$，那我们就去找有没有与其相对应的$0$，如果有，记录进答案；否则按照原来的$1$继续找。反之亦然。详情见$code$：

void add(int x) {//添加01串
	int p = 1;
	for(int i = 32; i >= 1; i--) {//转换成32位01串
		int ch = (x >> (i - 1)) & 1;//取出当前位
		if(ch == 1) x = x - (1 << (i - 1));//x随之改变（这一行可有可无）
		int &k = trie[p][ch];
		if(k == 0) k = ++tot;//正常插入操作
		p = k;
	}
	ed[p] = 1;
	return ;
}
int Search(int x) {
	int p = 1, cnt = 0;
	for(int i = 32; i >= 1; i--) {
		int ch = (x >> (i - 1)) & 1;
		if(ch == 1) x = x - (1 << (i - 1));//同插入，将x转为01串
		int k = trie[p][abs(ch-1)];//找与这一位相反的，因为想要让异或值更大，要尽可能让两个串不相等
		if(k) cnt += (1 << (i - 1)), p = k;//存在，存答案
		else p = trie[p][ch];//不存在，等于原来的
	}
	return cnt;//返回答案
}

有了这个思路，我们再来回顾此题。本题让我们找到任意两点之间的最长异或路径，那么我们可以先从根节点（假设为$1$）遍历整个树，求出根节点到每个点的异或和，再在所有的点中任选两个，使其异或值最大。

为什么呢？？请见下图：

从 $1$ 到 $root$ 的路径为 $A$，从 $2$ 到 $root$ 的路径为 $B$，从 $1$ 到 $2$ 的路径为 $C$。那么显而易见，$A\oplus B=C$。我们知道，$x\oplus x=0$，所以 $A$ 与 $B$ 相重合的部分就会被异或掉，留下的就只有 $C$。这道题就转化为了刚才的问题。详情见 $Code$：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
struct my_str {
	int End, Nxt, Value;
};
my_str edge[maxn*2];
int head[maxn];
int n, tot = 0;
int dp[maxn];
int trie[maxn*32][2];
void add(int u,int  v,int w) {
	edge[++ tot].Value = w;
	edge[tot].Nxt = head[u];
	edge[tot].End = v;
	head[u] = tot;
}
void dfs(int x, int fa) {
	for(int i = head[x]; i != -1; i = edge[i].Nxt) {
		int To = edge[i].End;
		if(To == fa) continue;
		dp[To] = dp[x] ^ edge[i].Value;
		dfs(To, x);
	}
	return ;
}
void Insert(int x) {
	int p = 1;
	for(int i = 31; i >= 0; i--) {
		int ch =((x >> i) & 1);
		int &k = trie[p][ch];
		if(k == 0) k = ++tot;
		p = k;
	}
	return ;
}
int Search(int x) {
	int p = 1;
	int cnt = 0;
	for(int i = 31; i >= 0; i--) {
		int ch = ((x >> i) & 1);
		int k = trie[p][ch ^ 1];
		if(k) cnt += (1 << i), p = k;
		else p = trie[p][ch];
	}
	return cnt;
}
int main() {
	scanf("%d", &n);
	memset(head, -1, sizeof(head));
	for(int i = 1; i < n; i++) {
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		add(u, v, w);
		add(v, u, w);//链式前向星建边
	}
	dp[1] = 0;
	dfs(1, 0);//求根到每一个点的异或值
	tot = 1;
	for(int i = 1; i <= n; i++) Insert(dp[i]);//同上
	int ans = -1;
	for(int i = 1; i <= n; i++) ans = max(ans, Search(dp[i]));
	printf("%d", ans);
	return 0;
}

AC自动机

\qquad AC自动机，一个让人看了十分兴奋的名字（雾）。它可以看做在Trie树上做KMP，结合了Trie树的结构和KMP的思想。主要解决多模式串匹配的问题。我们通过一个实例来深入理解AC自动机原理。

\qquad 假设现在有 $3$ 个模式串：$S_1=ABC$，$S_2=BCDF$，$S_3=CDE$，和一个文本串：$T=ABCDE$。我们首先要建造出这三个模式串的Trie树。

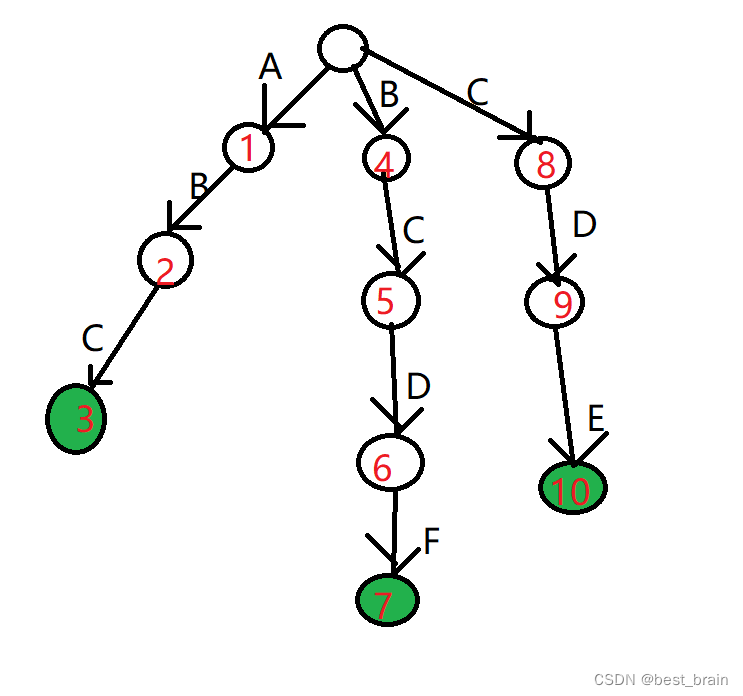
\qquad 然后我们在Trie树上找，首先找到了 $3$ 号节点，匹配到了 $ABC$ 这一模式串。接着呢？重回到根开始查找吗？那样效率显然太慢了，跳到 $5$ 号节点显然可以继续向下查找。可是让我们到了 $6$ 号节点，发现下面的字符匹配不上了。这时不得不回到根了吧？不！我们仍可以跳到 $9$ 号节点继续向下找到 $CDE$ 这一模式串。本次查找过程中，两次跳跃使得我们的查找效率大幅提升。

\qquad 我们若将这两次跳跃画成图上的指针，AC自动机就是所有跳跃指针全部画出后的状态。

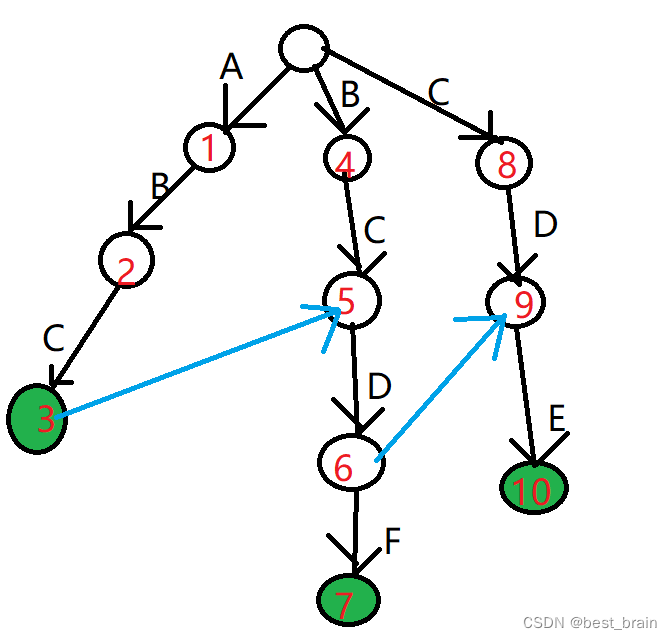
\qquad 上图中，我们只画出了最有用的两条指针。最终的AC自动机是比这个要复杂的。我们把AC自动机上的跳跃指针称为fail指针，又叫做失配指针。顾名思义，失配指针就是我们在Trie树上查找，失配之后跳跃的指针。AC自动机最重要的步骤就是构建失配指针。对于一个节点 $p$，我们要枚举一遍字符集，看是否存在 $tri{e}_p{,}_c$ 这一节点。若存在，对应上图 $2$ 号节点找到 $3$ 号节点的情况，我们便直接将 $fai{l}_p$ 的信息赋给 $tri{e}_p{,}_c$：$fai{l}_{tri{e}_p{,}_c}=tri{e}_{fai{l}_p}{,}_c$。若不存在，对应上图中 $6$ 号节点找到 $9$ 号节点的情况，因为 $tri{e}_p{,}_c$ 本身不存在，便不需要提前跳走，只需将 $fai{l}_p$ 的信息赋给 $tri{e}_p{,}_c$，相当于一个路径压缩的过程。

\qquad 整个过程可以用 $bfs$ 实现。

$Code:$

void Insert() {//插入模式串
	int p = 0;
	for(int i = 1; i <= sze; i ++) {
		int v = (int)(s[i] - 'a' + 1);
		if(!tr[p][v]) tr[p][v] = ++ tot;
		p = tr[p][v];
	}
	flag[p] ++;
}

void get_fail() {
	for(int i = 1; i <= 26; i ++)//把与根相连的节点存入队列中
		if(tr[0][i]) q.push(tr[0][i]), fail[tr[0][i]] = 0;
	fail[0] = 0;
	while(!q.empty()) {
		int p = q.front(); q.pop();
		for(int i = 1; i <= 26; i ++) {
			if(!tr[p][i]) tr[p][i] = tr[fail[p]][i];
			else fail[tr[p][i]] = tr[fail[p]][i], q.push(tr[p][i]);
		}
	}
}

后缀数组，后缀自动机，广义后缀自动机

\qquad here