在我们开始之前,以下是代码:
我和Minh Le一起做了这个项目。
为什么?
如果你是CS专业的人员,可能听过这句“不要使自己陷入_”的话无数次。CS有加密、标准库、解析器等等。我觉得现在还应该包含ML库。
不管事实如何,它仍然是一个值得学习的惊人的教训。人们现在认为TensorFlow和类似的库是理所当然的;把它们当成是一个黑盒子,让其运行。没有多少人知道后台发生了什么。这真是一个非凸的优化问题!不要停止搅拌那堆东西,直到它看起来合适为止(结合下图及机器学习系统知识去理解这句话)。
Tensorflow
TensorFlow是由Google开源的一个深度学习库。在TensorFlow的内核,有一个大的组件,将操作串在一起,行成一个叫做 运算符图 的东西。这个运算符图是一个有向图 G=(V,E) ,在某些节点 u1,u2,…,un,v∈V 和 e1,e2,…,en∈E,ei=(ui,v) 存在某些运算符将 u1,…,un 映射到 v 。
例如,如果我们有x + y = z,那么 (x,z),(y,z)∈E 。
这对于评估算术表达式非常有用。我们可以通过寻找运算符图中的 sinks来得到结果。 Sinks是诸如 v∈V,∄e=(v,u) 这样的顶点。换句话说,这些顶点没有到其它顶点的有向边。同样的, sources是 v∈V,∄e=(u,v) 。
对我们来说, 总是把值放在sources,值会传播到Sinks。
反向模式求导
如果认为我的解释不够好,这里有一些幻灯片。
求导是TensorFlow所需的许多模型的核心要求,因为需要它来运行 梯度下降算法。每个高中毕业的人都知道什么是求导; 它只是获取函数的导数,如果函数是由基本函数组成的复杂组合,那么就做 链式法则。
超级简单的概述
如果有一个这样的函数:
f(x,y) = x * y
那么关于X的求导将产生:
df(x,y)dx=y
关于Y的求导将产生:
df(x,y)dy=x
另外一个例子:
f(x1,x2,...,xn)=f(x)=xTx
这个导数是:
df(x)dxi=2xi
所以梯度就是:
∇xf(x)=2x
链式法则,譬如应用于复杂的函数 f(g(h(x))) :
df(g(h(x)))dx=df(g(h(x)))dg(h(x))dg(h(x))dh(x)dh(x)x
5分钟内反向模式
现在记住运算符图的DAG结构,以及上一个例子中的链式法则。如果要评估,我们可以看到:
x -> h -> g -> f
作为图表。会给出答案f。但是,我们也可以采取反向求解:
dx <- dh <- dg <- df
这看起来像链式法则!需要将导数相乘在一起,以获得最终结果。
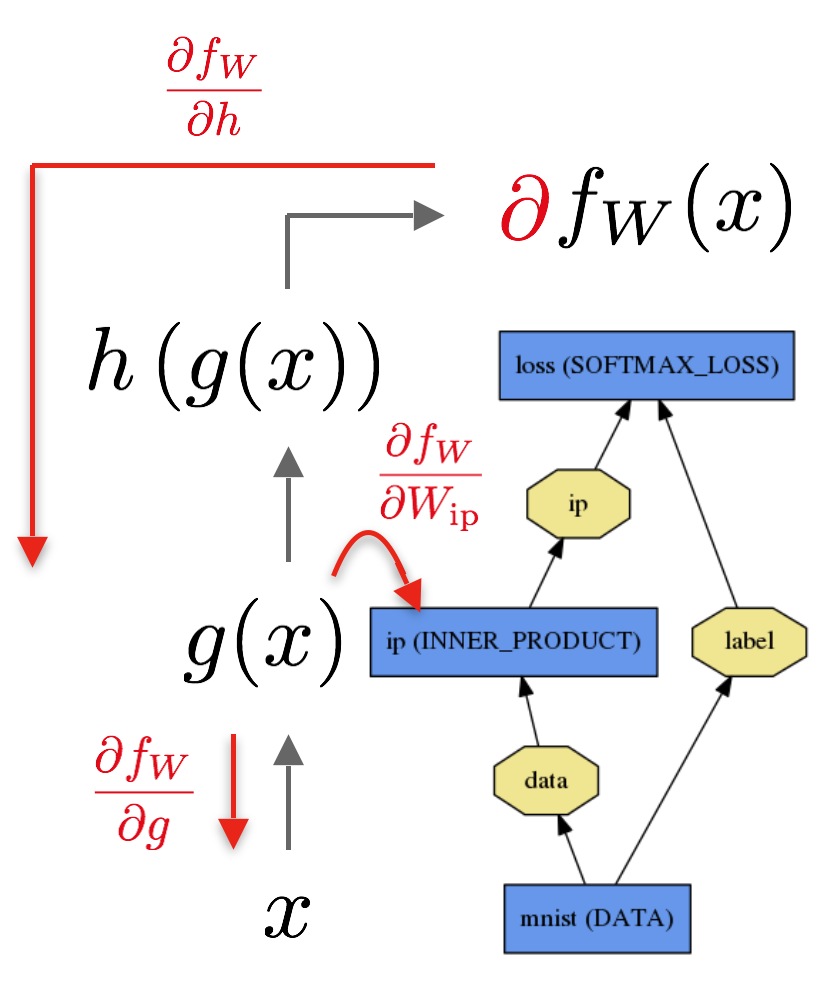
下图是一个运算符图的例子:
所以这基本上退化成图遍历问题。 有谁发觉拓扑排序和DFS / BFS吗?
所以要支持双向拓扑排序的话,需要包含一组父节点和一组子节点,Sinks是另一个方向的Sources, 反之亦然。
实施
在开学之前,Minh Le和我开始设计这个项目。我们决定使用Eigen 库后台进行线性代数运算。它们有一个称为MatrixXd的矩阵类。我们在这里使用它。
每个变量节点由var类表示:
class var {
// Forward declaration
struct impl;
public:
// For initialization of new vars by ptr
var(std::shared_ptr<impl>);
var(double);
var(const MatrixXd&);
var(op_type, const std::vector<var>&);
...
// Access/Modify the current node value
MatrixXd getValue() const;
void setValue(const MatrixXd&);
op_type getOp() const;
void setOp(op_type);
// Access internals (no modify)
std::vector<var>& getChildren() const;
std::vector<var> getParents() const;
...
private:
// PImpl idiom requires forward declaration of the class:
std::shared_ptr<impl> pimpl;
};
struct var::impl{
public:
impl(const MatrixXd&);
impl(op_type, const std::vector<var>&);
MatrixXd val;
op_type op;
std::vector<var> children;
std::vector<std::weak_ptr<impl>> parents;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
在这里,我们采用 pImpl惯用法,这意味着“通过指针来实现”。这在许多方面是非常好的,例如接口解耦实现, 当在堆栈上有一个本地shell接口时,允许在堆栈上实例化。pImpl的副作用是运行时间稍慢,但是编译时间缩短了很多。这让我们通过多个函数调用/返回来保持数据结构的持久性。像这样的树状数据结构应该是持久的。
有几个 枚举,告诉我们目前正在执行哪些操作:
enum class op_type {
plus,
minus,
multiply,
divide,
exponent,
log,
polynomial,
dot,
...
none // no operators. leaf.
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
执行该树评价的实际类称为expression:
class expression {
public:
expression(var);
...
// Recursively evaluates the tree.
double propagate();
...
// Computes the derivative for the entire graph.
// Performs a top-down evaluation of the tree.
void backpropagate(std::unordered_map<var, double>& leaves);
...
private:
var root;
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
在 反向传播的内部,有一些类似于此的代码:
backpropagate(node, dprev):
derivative = differentiate(node)*dprev
for child in node.children:
backpropagate(child, derivative)
- 1
- 2
- 3
- 4
- 5
这相当于做一个DFS; 你看到了吗?
为什么选择C ++?
事实上,C ++语言用于此不是特别合适。我们可以花 更少的时间用OCaml等功能性语言来开发。现在我明白了为什么Scala被用于机器学习,主要看你喜欢;)。
然而,C ++有明显的好处:
Eigen
例如,可以直接使用tensorflow的线性代数库,称之为Eigen。这是一个多模板惰性计算的线性代数库。类似于表达式树的样子,构建表达式,只有在需要时才会对表达式进行评估。然而,对于Eigen来说, 在编译的时候就确定何时使用模板,这意味着运行时间的减少。我特别赞赏写Eigen的人,因为审视模板的错误,让我的眼睛充血。
Eigen的代码看起来像:
Matrix A(...), B(...);
auto lazy_multiply = A.dot(B);
typeid(lazy_multiply).name(); // the class name is something like Dot_Matrix_Matrix.
Matrix(lazy_multiply); // functional-style casting forces evaluation of this matrix.
- 1
- 2
- 3
- 4
- 5
Eigen库是非常强大的,这就是为什么它是tensorflow自我使用的主要后台。这意味着除了这种惰性计算技术之外,还有其他方面的优化。
运算符重载
用Java开发这些库会非常好—没有shared_ptrs, unique_ptrs, weak_ptrs代码;我们可以采取 实际的,能胜任的,GC算法。使用Java开发可以节省许多开发时间,更不用说执行速度也会变得更快。可是,Java不允许运算符重载,因而它们就不能这样:
// These 3 lines code up an entire neural network!
var sigm1 = 1 / (1 + exp(-1 * dot(X, w1)));
var sigm2 = 1 / (1 + exp(-1 * dot(sigm1, w2)));
var loss = sum(-1 * (y * log(sigm2) + (1-y) * log(1-sigm2)));
- 1
- 2
- 3
- 4
- 5
顺便说一下,上面的是实际代码。这不是很漂亮吗?我认为 这比用于TensorFlow的python包装更漂亮。只想让你知道,这些也都是矩阵。
在Java语言中,这将是极其丑陋的,有着一堆add(), divide()…等等代码。更为重要的是, 用户将被隐式强制使用PEMDAS(括号 ,指数、乘、除、加、减),这一点上,C++的运算符表现的很好。
性能,而不是Bug
有一些东西,你可以在这个库中实际指定,TensorFlow没有明确的API,或者我不知道。比如,如果想训练某个特定子集的权重,可以只反向传播到感兴趣的具体来源。这对于卷积神经网络的 转移学习非常有用,一些大的网络,如VGG19网络,很容易用TensorFlow实现,其附加的几个额外的层的权重是根据新的域样本进行训练的。
基准
用Python的Tensorflow库,在Iris数据集上对10000个历史纪元进行分类训练,这些历史纪元具有相同的超参数,结果是:
- Tensorflow的神经网络
23812.5 ms - Scikit的神经网络库:
22412.2 ms - Autodiff的神经网络,迭代,优化:
25397.2 ms - Autodiff的神经网络,具有迭代,无优化:
29052.4 ms - Autodiff的神经网络,具有递归,无优化:
28121.5 ms
如此看来,令人惊讶的是,Scikit在所有这些中运行最快。这可能是因为我们没有做大量的矩阵乘法运算。也可能是因为tensorflown不得不通过变量初始化采用额外的编译步骤。或者,也许可能不得不在python中运行循环,而不是在C语言中(python循环 真的很糟糕!)。我自己也不确定这到底是因为什么。
我完全意识到这绝对不是一个全面的基准测试,因为它只适用于在特定情况下的单个数据点。不过,这个库的性能并不是最先进的技术,因为我们不希望把自己卷进TensorFlow。






















 1560
1560

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








