Semantic Hierarchy-Aware Segmentation 语义层次感知分割

Semantic Hierarchy-Aware Segmentation 语义层次感知分割

Liulei Li, Wenguan Wang, Tianfei Zhou, Ruijie Quan, Yi Yang

最近阅读文章，发现一篇很有创新的文章，故结合自己理解分享一下。

摘要：人类能够在观察中识别结构化关系，使我们能够将复杂的场景分解为更简单的部分，并在多个层面上抽象视觉世界。然而，在当前的语义分割文献中，人类感知的这种分层推理能力在很大程度上仍未得到探索。现有的作品通常知道扁平化标签并专门区分每个像素的所有语义类别。在这项工作中，我们转而解决分层语义分割（HSS）问题，目的是根据类层次结构提供视觉观察的结构化、像素级描述。我们设计了 HSSN，一个通用的 HSS 框架，它解决了这项任务中的两个关键问题：i）如何有效地将现有的与层次结构无关的分割网络适应 HSS 设置，以及 ii）如何利用类层次结构来规范 HSS 网络学习。为了解决 i)，HSSN 直接将 HSS 作为像素级多标签分类任务，只为当前的分割模型带来最小的架构变化。为了解决 ii)，HSSN 首先探索层次结构的固有属性作为训练目标，强制分段预测遵守层次结构。此外，通过一组层次结构引起的边距约束，HSSN 有效地重塑了学习到的像素嵌入空间，从而生成层次结构感知的像素表示并最终促进结构化分割。在 HSSN 的基础上，我们进一步利用语义标签之间的互斥关系，并通过更有意义的约束强化基于边际的正则化策略，从而产生了 HSSN+，一种更有效的 HSS 框架。我们对六个具有不同类层次结构、网络架构和主干的语义分​​割数据集（即 Mapillary Vistas 2.0、Cityscapes、LIP、PASCAL-Person-Part、PASCAL-Part-58 和 PASCAL-Part-108）进行了广泛的实验，结果证实了我们算法的泛化性和优越性。

这篇文章主要的创新有以下几点：

1. 将单个分类器函数softmax替换为多个独立的二分类函数sigmoid;
2. 将像素标记为多分类，一个像素对应树结构的多种标签；
3. 对于树状层次结构提出三条约束并改进损失函数；
4. 利用层次结构重塑采样编码器函数fENC；
   
   传统的层次分割方法首先采用编码器 fENC 将图像 I 映射到密集特征张量 I = fENC(I) ∈ RH×W×C
   使用分割头fSEG得到得分图Y = softmax(fSEG(I)) ∈ [0, 1]H×W×|V|。此文则是用S = sigmoid(fSEG(I)) ∈ [0, 1]H×W×|V|代替Y = softmax(fSEG(I)) ∈ [0, 1]H×W×|V|。两者函数的区别就我个人理解，softmax是一个单一的分类器函数，而sigmoid则是多个独立的二分类函数。

逐像素层次分割学习策略

此文提出了两个学习策略，其一是逐像素层次分割学习策略。文章在提出三个约束。

个人对三个约束的理解是
约束一：像素的分类必须是父类的子类，正相关性。
约束二：如果像素不属于某一类，其也不属于所有的父类，负相关性。
约束三：同级节点只有一个为正，排他性。

文章同时介绍了几个常用的损失函数及模型所用算法的推导
分类交叉熵损失函数：


根据约束一、二，将得分函数更新为：


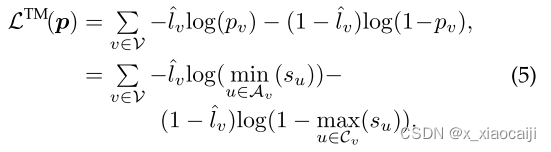
受到焦点树的启发，提出了最小焦点树损失，主要是增加了一个调节因子，能够介绍分类良好的损失，着重关注分类困难的分类像素。

随后加入约束三，得到改进后的最小焦点树损失函数




损失函数的得分分数的定义，个人不知道怎么理解。但是我从损失函数的角度解析公式。如果是正确的节点则选择最小的概率，如果是错误的节点则选择最大的概率。这么做的原因是这样会使损失函数变大，从而受到惩罚力度加大，多次训练后，则可以将损失逐步变小。

逐像素层次表示学习策略

逐像素表示学习策略主要有两个重要点，分别是控制类间距离，及类别之间距离。分别用如下公式表示：

该损失在一组像素三元组 {i, i+, i−} 上进行优化，其中 i, i+, i− 分别是锚点、正像素样本和负像素样本。 {i, i+, i−} 从整个训练批次中采样。在我们的树三元组损失中，与负像素相比，正样本在语义上与锚像素更相似（即，在 T 中更接近）。由公式可知，迫使m大于 ⟨i, i−⟩ 和 ⟨i, i+⟩ 之间的间隙。此为类间间隙。

其中κ指的是T的深度。这里mε = 1/2κ被设置为类内方差容差的常数，即最大类内距离，而mτ=(ψ(ˆv⋄, ˆv− ⋄) ) − ψ(ˆv⋄, ˆv+ ⋄ ))/2κ 是动态违规边际，它是根据类层次结构 T 上 i、i+ 和 i− 之间的语义关系计算的。其中mτ的定义个人不是很清楚。

类别距离公式如下;


类别距离公式的含义跟类间距离相似。不做赘述。

后续的结果可自行查看文章，文章链接如下https://ieeexplore.ieee.org/document/10316583