（1）信息熵，条件熵，信息增益，信息增益率

介绍信息熵和信息增益之前，先介绍信息增量的概念

1、信息量

定义：信息多少的量度，与事件发生的概率相关。

公式：信息量用$I$表示， 记事件A发生的概率为p，则事件A的信息量计算公式：
$$I_A=-{\log }_2(p)$$

例子 :比如说，我们掷骰子，点数为一事件的概率为$\frac{1}{6}$, 那么该事件的信息量为：
$$I_B=-{\log }_2(\frac{1}{6})={\log }_{2}6\approx 2.6$$

2、信息熵

定义：信息熵是信息量的期望值，描述的是不确定性。

公式：由定义我们可以得到熵的计算公式：
$$E(S)=-\sum _{i=1}^n{p}_i\times {\log }_2(p_i)$$

$S：样本空间$
$p_i:事件i发生的概率$

3、信息熵冗余度

$$1-E(S)$$

例子：
举一个的例子：对游戏活跃用户进行分层，分为高活跃、中活跃、低活跃三种层次。
模式A按照用户比例分别为20%，30%，50%划分。
模式B按照用户比例分别为5%，5%，90%划分。

$模式A划分方式下游戏的熵为：$
$$E(S)=-0.2\times {\log }_{2}0.2-0.3\times {\log }_{2}0.3-0.5\times {\log }_{2}0.5\approx 1.485$$

$模式B划分方式下游戏的熵为：$
$$E(S)=-0.05\times {\log }_{2}0.05-0.05\times {\log }_{2}0.05-0.9\times {\log }_{2}0.9\approx 0.569$$

因此可以知道，模式A下的游戏的熵值更大，不确定性更强，游戏更加丰富。

4、条件熵

定义：已知随机变量 X 的条件下随机变量 Y 的不确定性， 随机变量X给定条件下 Y 的条件概率分布的熵对 X 的数学期望。
公式：条件熵用$H(Y|X)$表示，计算公式为：
$$H(Y|X)=\sum _{i=1}^n{p}_i\times H(Y|X=x_i)$$

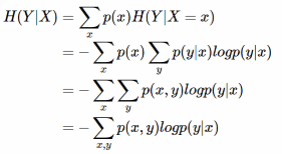
条件熵 H(Y|X)相当于联合熵 H(X,Y)减去单独的熵 H(X)，即H(Y|X)=H(X,Y)−H(X)：

eg：有以下数据

整体熵为：
$$E(S)=-\frac{5}{15}\times {\log }_2(\frac{5}{15})-\frac{10}{15}\times {\log }_2(\frac{10}{15})\approx 0.9182$$

男性：
$$E(S_1)=-\frac{3}{8}\times {\log }_2(\frac{3}{8})-\frac{5}{8}{\log }_2(\frac{5}{8})\approx 0.9543$$

女性：
$$E(S_2)=-\frac{2}{7}\times {\log }_2(\frac{2}{7})-\frac{5}{7}\times {\log }_2(\frac{5}{7})\approx 0.8631$$

性别条件熵：
$$E(S,A)=\frac{8}{15}\times E(S_1)+\frac{7}{15}\times E(S_2)\approx 0.9118$$

5、信息增益

定义：信息增益是信息熵的差值。
当我们使用机器学习模型的时候，特征值的正确选择能够提高模型的准确率，那么最有力的特征值使得识别率最高，也就是加入了特征值以后整体熵就变小了，减少的熵值就称作信息增益。

公式：信息增益用$Grain(S,A)$表示，计算公式：
$$Grain(S,A)=E(S)-E(S,A)=E(S)-H(S|A)$$

eg:有条件熵中的例子可知，加入性别以后的信息增益为：
$$Gain(S,A)=E(S)-E(S,A)=0.9184-0.9118\approx 0.0064$$

6、信息增益率

定义：某一特征值的信息增益与该特征值的信息熵之比。

公式：信息增益率用$E_{\gamma }(S,A)$表示，计算公式：
$$E_{\gamma }(S,A)=\frac{Gain(S,A)}{E(A)}$$

eg：性别信息增益率
性别熵：
$$E(A)=-\frac{8}{15}\times {\log }_2(\frac{8}{15})-\frac{7}{15}\times {\log }_2(\frac{7}{15})\approx 0.9968$$

$$E_{\gamma }(S,A)=\frac{Gain(S,A)}{E(A)}=\frac{0.0064}{0.9968}\approx 0.0064$$

7、基尼系数

定义：反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。
公式：基尼系数用$Gini(D)$表示，计算公式：
$$Gini(D)=\sum _{i=1}^n{p}_i\times (1-p_i)=\sum _{i=1}^n{p}_i^2$$
eg:

8、附件

计算熵算法：

import math

def entropy(*c):
    if (len(c)<=0):
        return -1
    result = 0;
    for x in c:
        result += (-x)*math.log(x,2)
    return result


print(entropy(0.99,0.01))
print(entropy(0.5,0.5))
print(entropy(0.333,0.333,0.333))

9、参考文献：

https://baike.baidu.com/item/%E4%BF%A1%E6%81%AF%E9%87%8F/420401
https://zhuanlan.zhihu.com/p/41134986
https://blog.csdn.net/guomutian911/article/details/78599450
https://www.cnblogs.com/qcloud1001/p/6735352.html
https://cloud.tencent.com/developer/article/1526414