量子力学摘记1

1. 波函数的统计诠释

\qquad 在量子力学中用波函数 $\Psi (\mathbf{r},t)$ 表征微观粒子的运动状态，或者说，波函数描写了体系的量子态$\text{(quantum state)}$。

\qquad 为人们所普遍接受的对于波函数的解释是由玻恩提出的，波函数的统计诠释指出：$|\Psi (\mathbf{r},t){|}^2$ 给出了在 $t$ 时刻位于 $\mathbf{r}$ 处发现这个粒子的概率 。

在空间某点 $\mathbf{r}$ 处附近找到粒子的概率该区域的大小有关：
（1）在一个体积元 $x\to x+\mathrm{d}x,y\to y+\mathrm{d}y,z\to z+\mathrm{d}z$ 内，$\Psi (\mathbf{r},t)$ 可认为是不变的
（2）粒子在该区域内出现的概率正比于体积元的大小 $\mathrm{d}V=\mathrm{d}x\mathrm{d}y\mathrm{d}z$，也就是 $|\Psi (\mathbf{r},t){|}^2\mathrm{d}V$
（3）$|\Psi (\mathbf{r},t){|}^2$ 表示 $t$ 时刻位于 $\mathbf{r}$ 处单位体积内粒子出现的概率（假设满足归一性）

取自于Griffiths《量子力学概论》图1.2
假设粒子沿 $x$ 轴运动，粒子波函数为 $\Psi (x,t)$，那么 $|\Psi (x,t){|}^2$ 给出了在 $t$ 时刻位于 $x$ 处发现这个粒子的概率。
或者更精确地说， ∫ a b ∣ Ψ ( x , t ) ∣ 2 d x = { \displaystyle\int_a^b\vert\Psi(x,t)\vert^2\mathrm{d}x=\{ ∫ab​∣Ψ(x,t)∣2dx={在 $t$ 时刻发现粒子处于 $a$ 和 $b$ 之间的概率.$\}$（后文不再具体区分概率与概率密度的概念）

取自于程守洙《普通物理学》图13-24
电子双缝干涉图像，曝光时间：$(a)0.01s(b)0.1s(c)3s(d)20s(e)70s$
随着曝光时间的延长，电子数目逐渐增多，在底片上的分布逐渐形成了干涉图样，显示出电子的波动性
可见，电子在底片上各处出现的概率具有一定的分布

\qquad

2. 态叠加原理

\qquad 量子态叠加原理可以表述为：如果 ${\Psi }_1,{\Psi }_2,\cdots ,{\Psi }_n,\cdots$ 都是体系的可能状态，那么它们的线性叠加态 $\Psi ={\sum }_i{c}_i{\Psi }_i$ 也是这个体系的可能状态，处于线性叠加态 $\Psi$ 的体系部分地处于态 ${\Psi }_1,{\Psi }_2,\cdots ,{\Psi }_n,\cdots$ 中，相应的概率分别为 $|c_1{|}^2,|c_2{|}^2,\cdots ,|c_n{|}^2,\cdots$。

态叠加原理指的是“波函数的线性叠加”，而不是概率的叠加。

\qquad 以电子的双缝衍射为例：

$(1)$ 用 ${\Psi }_1$ 表示粒子穿过缝 $1$ 狭缝到达屏 $\text{S}$ 的状态，用 ${\Psi }_2$ 表示粒子穿过缝 $2$ 狭缝到达屏 $\text{S}$ 的状态，用 $\Psi$ 表示粒子穿过双缝到达屏 $\text{S}$ 的状态。那么，$\Psi$ 就可以写为 ${\Psi }_1$ 和 ${\Psi }_2$ 的线性叠加，即 $\Psi =c_1{\Psi }_1+c_2{\Psi }_2$。

$(2)$ 如果 ${\Psi }_1$ 和 ${\Psi }_2$ 是体系的可能状态，那么线性叠加态 $\Psi =c_1{\Psi }_1+c_2{\Psi }_2$ 也是这个体系的一个可能状态，此时处于线性叠加态的粒子是既处在态 ${\Psi }_1$，又处在态 ${\Psi }_2$。

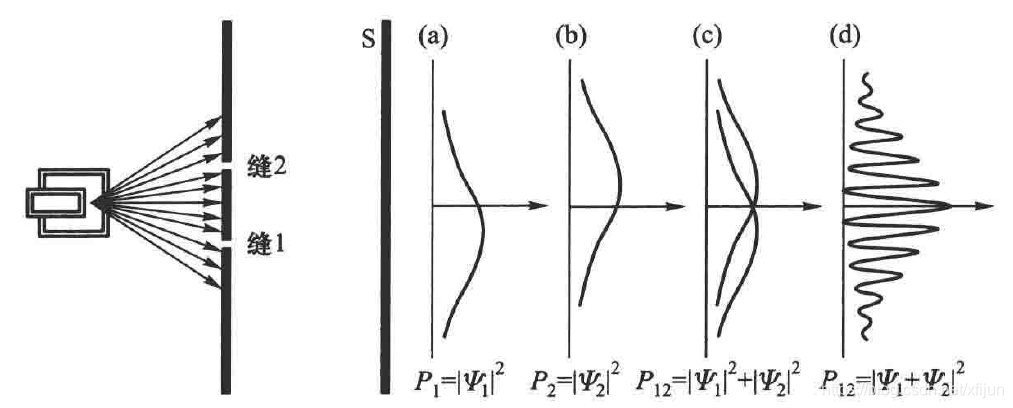
取自于程守洙《普通物理学》图13-25
图中的线性叠加态 $\Psi ={\Psi }_1+{\Psi }_2,c_1=c_2=1$
如果只开缝1，$\Psi ={\Psi }_1$（未处于叠加态），其概率密度为 $P_1=|\Psi {|}^2=|{\Psi }_1{|}^2$，如 $(a)$ 所示；
如果只开缝2，$\Psi ={\Psi }_2$（未处于叠加态），其概率密度为 $P_2=|\Psi {|}^2=|{\Psi }_2{|}^2$，如 $(b)$ 所示；
如果同时打开两缝，按经典统计理论应该如 $(c)$ 所示；而实际上由于量子相干性，处于叠加态中的态 ${\Psi }_1$ 和态 ${\Psi }_2$ 会相互干涉，其概率密度包含了干涉项，如图 $(d)$ 所示
实验可参考《Controlled double-slit electron diffraction》

\qquad 按照态叠加原理，粒子在屏 $\text{S}$ 上一点 $\text{P}$ 出现的概率密度为：

$\begin{array}{rl}|\Psi {|}^2& =|c_1{\Psi }_1+c_2{\Psi }_2{|}^2=(c_1^{\ast }{\Psi }_1^{\ast }+c_2^{\ast }{\Psi }_2^{\ast })(c_1{\Psi }_1+c_2{\Psi }_2)\\ & =|c_1{\Psi }_1{|}^2+|c_2{\Psi }_2{|}^2+c_1^{\ast }{c}_2{\Psi }_1^{\ast }{\Psi }_2+c_1{c}_2^{\ast }{\Psi }_1{\Psi }_2^{\ast }\end{array}$

\qquad 其中，$|c_1{\Psi }_1{|}^2$ 是粒子穿过缝 $1$ 出现在 $\text{P}$ 点的概率密度，$|c_2{\Psi }_2{|}^2$ 是粒子穿过缝 $2$ 出现在 $\text{P}$ 点的概率密度，$c_1^{\ast }{c}_2{\Psi }_1^{\ast }{\Psi }_2$ 和 $c_1{c}_2^{\ast }{\Psi }_1{\Psi }_2^{\ast }$ 是 ${\Psi }_1$ 和 ${\Psi }_2$ 的干涉项。

粒子穿过双狭缝后在屏 $\text{S}$ 上一点 $\text{P}$ 出现的概率密度 $|\Psi {|}^2$，一般不等于粒子穿过缝 $1$ 和缝 $2$ 到达 $\text{P}$ 点的概率密度之和 $|c_1{\Psi }_1{|}^2+|c_2{\Psi }_2{|}^2$
电子衍射图像的结果也证实了干涉项的存在

\qquad 量子力学中，微观粒子的状态用波函数描写，而决定粒子状态变化的方程是薛定谔方程。
\qquad

3. 薛定谔方程

\qquad 德布罗意认为微观粒子也具有波动性，并将“粒子”与“波”之间建立起联系，即粒子的能量 $E$ 和动量 $\mathbf{p}$ 与波的频率 $\nu$ 和波长 $\lambda$ 之间具有如下关系：

$\{\begin{array}{ll}E=h\nu =\hslash \omega & (\hslash =\frac{h}{2\pi })\\ & \\ \mathbf{p}=\hslash \mathbf{k}& (p=\hslash k=\hslash \frac{2\pi }{\lambda }=\frac{h}{\lambda })\end{array}$

\qquad 由上述德布罗意关系可知，与自由粒子相联系的波（因为其频率 $\nu$ 和波矢 $\mathbf{k}$ 都不变）是一个平面波。

平面波的频率 $\nu$ 和波矢 $\mathbf{k}$ 都不随时间变化
与之对应的是，自由粒子的能量 $E$ 和动量 $\mathbf{p}$ 也不随时间变化

$\bullet$频率为 $\omega$、相移常数为 $k$、沿 $x$ 方向传播的平面波为 ${\Psi }_k(x,t)=A\cos (kx-\omega t)$

\qquad 将平面波写成复数形式 ${\Psi }_k(x,t)=A{e}^{i(kx-\omega t)}$，再分别求 $x,t$ 的偏导，就可以得到以下关系：

$\{\begin{array}{ll}& -i\hslash \frac{\partial }{\partial x}{\Psi }_k=\hslash k{\Psi }_k\\ & \\ & i\hslash \frac{\partial }{\partial t}{\Psi }_k=\hslash \omega {\Psi }_k\end{array}$

也就是说，将算符 $-i\hslash \frac{\partial }{\partial x}$ 和 $i\hslash \frac{\partial }{\partial t}$ 作用在函数 ${\Psi }_k$ 上，就得到了粒子的动量 $\mathbf{p}$ 和能量 $E$。

\qquad
$\bullet$考虑一般情况，描述自由粒子的平面波为 ${\Psi }_k(\mathbf{r},t)=A{e}^{i(\mathbf{k}\cdot \mathbf{r}-\omega t)}$

\qquad 由德布罗意关系，将平面波 ${\Psi }_k(\mathbf{r},t)=A{e}^{i(\mathbf{k}\cdot \mathbf{r}-\omega t)}$ 中代表波动性的 $\omega$ 和 $\mathbf{k}$ 替换为代表粒子性的 $E$ 和 $\mathbf{p}$，就得到了德布罗意波的表达式：

$\Psi (\mathbf{r},t)=A{e}^{\frac{i}{\hslash }(\mathbf{p}\cdot \mathbf{r}-Et)}$

\qquad 分别对 ${\Psi }_k(\mathbf{r},t)$ 求 $\mathbf{r},t$ 的偏导，可得到：

$\{\begin{array}{l}-i\hslash \nabla {\Psi }_k=\hslash \mathbf{k}{\Psi }_k=\mathbf{p}{\Psi }_k\\ \\ i\hslash \frac{\partial }{\partial t}{\Psi }_k=\hslash \omega {\Psi }_k=E{\Psi }_k\end{array}$

\qquad 令 $\hat{\mathbf{p}}$ 表示动量算符 $-i\hslash \nabla$，令 $\hat{E}$ 表示能量算符 $i\hslash \frac{\partial }{\partial t}$，也就是：

$\{\begin{array}{ll}{\hat{\mathbf{p}}}^2=\hat{\mathbf{p}}\cdot \hat{\mathbf{p}}& ⟷-{\hslash }^2{\nabla }^2\\ & \\ \hat{E}& ⟷-i\hslash \frac{\partial }{\partial t}\end{array}$

\qquad 由经典力学中自由粒子能量与动量之间的关系 $E=\frac{1}{2m}{\mathbf{p}}^2$，将能量和动量分别用算符 $\hat{E}$ 和 $\hat{\mathbf{p}}$ 替换再作用到波函数 $\Psi (\mathbf{r},t)$ 上，就得到：

$\hat{E}\Psi =\frac{1}{2m}{\hat{\mathbf{p}}}^2\Psi$

\qquad 也就是自由粒子薛定谔方程：$i\hslash \frac{\partial }{\partial t}\Psi =-\frac{{\hslash }^2}{2m}{\nabla }^2\Psi$

可以验证德布罗意波 ${\Psi }_k(\mathbf{r},t)=A{e}^{\frac{i}{\hslash }(\mathbf{p}\cdot \mathbf{r}-Et)}$ 满足该方程

\qquad 假设粒子在力场中的势能为 $V(\mathbf{r})$，此时粒子能量与动量之间的关系为 $E=\frac{{\mathbf{p}}^2}{2m}+V(\mathbf{r})$。将能量和动量用算符 $\hat{E}$ 和 $\hat{\mathbf{p}}$ 替换再作用到波函数 $\Psi (\mathbf{r},t)$ 上，就得到了薛定谔方程：

$i\hslash \frac{\partial }{\partial t}\Psi =-\frac{{\hslash }^2}{2m}{\nabla }^2\Psi +V(\mathbf{r})\Psi$

经典力学中总能量 $E=\frac{{\mathbf{p}}^2}{2m}+V(\mathbf{r})$ 称为哈密顿量，对应的哈密顿算符 $\hat{H}⟷-\frac{{\hslash }^2}{2m}{\nabla }^2+V(\mathbf{r})$
　
薛定谔方程可以写成算符形式：$i\hslash \frac{\partial }{\partial t}\Psi =\hat{H}\Psi$，即：$i\hslash \frac{\partial }{\partial t}\Psi (\mathbf{r},t)=\hat{H}\Psi (\mathbf{r},t)$

\qquad

4. 定态薛定谔方程

\qquad 具有确定能量值的状态称为“定态”，定态波函数的时空变量可以分离。如果势能 $V(\mathbf{r})$ 不含时间，采用分离变量法将 $\Psi (\mathbf{r},t)=\psi (\mathbf{r})f(t)$ 代入薛定谔方程：

$\frac{i\hslash }{f}\frac{\mathrm{d}f}{\mathrm{d}t}=\frac{1}{\psi }\left[-\frac{{\hslash }^2}{2m}{\nabla }^2\psi +V(\mathbf{r})\psi \right]$

将 $\Psi (\mathbf{r},t)=\psi (\mathbf{r})f(t)$ 代入薛定谔方程 $i\hslash \frac{\partial }{\partial t}\Psi =\hat{H}\Psi$
　
$⟹i\hslash \frac{\mathrm{d}f(t)}{\mathrm{d}t}\psi (\mathbf{r})=f(t)\hat{H}\psi (\mathbf{r})$，　　两个边同时除 $\psi (\mathbf{r})f(t)$
　
$⟹\frac{i\hslash }{f(t)}\frac{\mathrm{d}f(t)}{\mathrm{d}t}=\frac{1}{\psi (\mathbf{r})}\hat{H}\psi (\mathbf{r})=E$

\qquad 等式的左边只是 $t$ 的函数，右边只是 $\mathbf{r}$ 的函数，而 $t$ 和 $\mathbf{r}$ 是相互独立的变量。只有等式两边都等于同一常量时，等式才能被满足。若以 $E$ 表示这个常量，那么：

$(a)$ 由等式的左边等于 $E$，可得：

$Ef(t)=i\hslash \frac{\mathrm{d}f(t)}{\mathrm{d}t}⟶f(t)=C{e}^{-i\frac{E}{\hslash }t}$

$(b)$ 由等式的右边等于 $E$，可得到定态$\text{(time independent)}$薛定谔方程：

$-\frac{{\hslash }^2}{2m}{\nabla }^2\psi (\mathbf{r})+V(\mathbf{r})\psi (\mathbf{r})=E\psi (\mathbf{r})$

\qquad 可得到定态薛定谔方程的特解为：

$\Psi (\mathbf{r},t)=\psi (\mathbf{r})e^{-i\frac{E}{\hslash }t}$

\qquad 这个波函数的角频率 $\omega =\frac{E}{\hslash }$ 是确定的。根据德布罗意关系，$E$ 就是体系处于该波函数所描写状态时的能量。此时的状态为定态$\text{(stationary states)}$，函数 $\Psi (\mathbf{r},t)=\psi (\mathbf{r})e^{-i\frac{E}{\hslash }t}$ 为定态波函数。

在定态中，由于概率密度满足 $|\Psi (\mathbf{r},t){|}^2=|\psi (\mathbf{r}){|}^2$ 不依赖时间，计算的时候完全可以去掉 $e^{-i\frac{E}{\hslash }t}$，简单地用不含指数时间因子的 $\psi (\mathbf{r})$ 代替 $\Psi (\mathbf{r},t)$ 。在这种意义上，函数 $\psi (\mathbf{r})$ 也可称为“波函数”；而真正的波函数 $\Psi (\mathbf{r},t)$ 总是含有指数时间因子。

\qquad

• 定态是具有确定总能量的态

\qquad 引入哈密顿算符 $\hat{H}=-\frac{{\hslash }^2}{2m}{\nabla }^2+V(\mathbf{r})$，就可将定态薛定谔方程 $-\frac{{\hslash }^2}{2m}{\nabla }^2\psi (\mathbf{r})+V(\mathbf{r})\psi (\mathbf{r})=E\psi (\mathbf{r})$ 写成本征方程：

$\hat{H}\psi (\mathbf{r})=E\psi (\mathbf{r})$

\qquad 其中，常量 $E$ 称为算符 $\hat{H}$ 的本征值，$\psi (\mathbf{r})$ 称为算符 $\hat{H}$ 属对应于本征值 $E$ 的本征函数。

$(1)$ 总能量的期望值 $⟨H⟩=\int {\psi }^{\ast }\hat{H}\psi \mathrm{d}\mathbf{r}=E\int {\psi }^{\ast }\psi \mathrm{d}\mathbf{r}=E\int |\psi {|}^2\mathrm{d}\mathbf{r}=E\int |\Psi {|}^2\mathrm{d}\mathbf{r}=E$
　
$(2)$ 又由 ${\hat{H}}^2\psi =\hat{H}(\hat{H}\psi )=\hat{H}(E\psi )=E(\hat{H}\psi )=E^2\psi$

$⟹⟨H^2⟩=\int {\psi }^{\ast }{\hat{H}}^2\psi \mathrm{d}\mathbf{r}=E^2\int |\psi {|}^2\mathrm{d}\mathbf{r}=E^2\int |\Psi {|}^2\mathrm{d}\mathbf{r}=E^2$

\qquad 总能量的涨落（也就是“方差/标准差”） $\Delta H=\sqrt{⟨H^2⟩-⟨H{⟩}^2}=0$

\qquad 这就说明每个样本有同样的值，对总能量的每次测量结果都是一个确定的值 $E$

\qquad

• 定态薛定谔方程的一般解是分离变量解的线性组合

\qquad 一般来说，本征方程有一系列（无穷多个）本征值，以 $E_n$ 表示体系能量算符的第 $n$ 个本征值，${\psi }_n(\mathbf{r})$ 是与 $E_n$ 对应的本征函数，则体系的第 $n$ 个定态波函数为：

${\Psi }_n(\mathbf{r},t)={\psi }_n(\mathbf{r})e^{-i\frac{E_n}{\hslash }t}$

\qquad 薛定谔方程的一般解，可以写为这些定态波函数的线性叠加（复数 $c_n$ 是常系数）：

$\Psi (\mathbf{r},t)=\sum _n{c}_n{\Psi }_n(\mathbf{r},t)=\sum _n{c}_n{\psi }_n(\mathbf{r})e^{-i\frac{E_n}{\hslash }t}$

（1）一旦得到了薛定谔方程的“分离变量解”，便可以构造出一般解。
（2）尽管分离变量解 ${\Psi }_n(\mathbf{r},t)={\psi }_n(\mathbf{r})e^{-i\frac{E_n}{\hslash }t}$ 自身是定态解（即概率和期望值的计算过程不依赖时间，也就是可以用 $\psi (\mathbf{r})$ 代替 $\Psi (\mathbf{r},t)$ 进行计算），但是一般解 $\Psi (\mathbf{r},t)={\sum }_n{c}_n{\psi }_n(\mathbf{r})e^{-i\frac{E_n}{\hslash }t}$ 并不具有这一性质。
　
例：$\Psi (x,t)=c_1{\psi }_1(x)e^{-i\frac{E_1}{\hslash }t}+c_2{\psi }_2(x)e^{-i\frac{E_2}{\hslash }t}$，并假设 $c_n$ 和 ${\psi }_n(x)$ 为实数，那么
　
　　$\begin{array}{rl}|\Psi (\mathbf{r},t){|}^2& =(c_1{\psi }_1{e}^{-i\frac{E_1}{\hslash }t}+c_2{\psi }_2{e}^{-i\frac{E_2}{\hslash }t})(c_1{\psi }_1{e}^{i\frac{E_1}{\hslash }t}+c_2{\psi }_2{e}^{i\frac{E_2}{\hslash }t})\\ & =c_1^2{\psi }_1^2+c_2^2{\psi }_2^2+c_1{c}_2{\psi }_1{\psi }_2{e}^{i\frac{E_1-E_2}{\hslash }t}+c_1{c}_2{\psi }_1{\psi }_2{e}^{-i\frac{E_1-E_2}{\hslash }t}\\ & =c_1^2{\psi }_1^2+c_2^2{\psi }_2^2+2c_1{c}_2{\psi }_1{\psi }_2\cos (\frac{E_1-E_2}{\hslash }t)\end{array}$
　
　　这显然不是一个定态，概率密度是以正弦的形式振动。

\qquad

• 波函数随时间的变化 —— 时间演化算符

\qquad 波函数随时间的变化取决于薛定谔方程 $i\hslash \frac{\partial }{\partial t}\Psi (\mathbf{r},t)=\hat{H}\Psi (\mathbf{r},t)$，假设哈密顿量 $\hat{H}$ 与时间无关，且其本征方程满足：

$\hat{H}{\psi }_n(\mathbf{r})=E_n{\psi }_n(\mathbf{r}),n=1,2,\cdots$

\qquad 薛定谔方程 $i\hslash \frac{\partial }{\partial t}\Psi (\mathbf{r},t)=\hat{H}\Psi (\mathbf{r},t)$ 是时间 $t$ 的一阶微分方程，因此只需给定初始时刻 $t_0=0$ 的波函数 $\Psi (\mathbf{r},0)$，就可以求出任意时刻 $t$ 的波函数 $\Psi (\mathbf{r},t)$，那么

$\Psi (\mathbf{r},0)=\sum _n{c}_n{\Psi }_n(\mathbf{r},0)=\sum _n{c}_n{\psi }_n(\mathbf{r})$

薛定谔方程的一般解为 $\Psi (\mathbf{r},t)=\sum _n{c}_n{\Psi }_n(\mathbf{r},t)=\sum _n{c}_n{\psi }_n(\mathbf{r})e^{-i\frac{E_n}{\hslash }t}$

\qquad 以 $\Psi (\mathbf{r},0)$ 作为初始条件，并引入时间演化算符 $\hat{U}(t)=e^{-i\frac{\hat{H}}{\hslash }t}$，那么

$\Psi (\mathbf{r},t)=\hat{U}(t)\Psi (\mathbf{r},0)=e^{-i\frac{\hat{H}}{\hslash }t}\Psi (\mathbf{r},0)$

或者表示为 $|\psi (t)⟩=\hat{U}(t)|\psi (0)⟩$
　
证明过程如下：
由泰勒级数展开式 $e^{\hat{A}}=\sum _{k=0}^{\infty }\frac{{\hat{A}}^k}{k!}$，时间演化算符 $\hat{U}(t)=e^{-i\frac{\hat{H}}{\hslash }t}=\sum _{k=0}^{\infty }\frac{{\left(-i\frac{t}{\hslash }\right)}^k}{k!}{\hat{H}}^k$
　
$\begin{array}{rl}\Psi (\mathbf{r},t)=\hat{U}(t)\Psi (\mathbf{r},0)& =e^{-i\frac{\hat{H}}{\hslash }t}\Psi (\mathbf{r},0)\\ & =e^{-i\frac{\hat{H}t}{\hslash }}\sum _n{c}_n{\psi }_n(\mathbf{r})\\ & =\sum _{k=0}^{\infty }\frac{{\left(-i\frac{t}{\hslash }\right)}^k}{k!}{\hat{H}}^k\sum _n{c}_n{\psi }_n(\mathbf{r})\\ & =\sum _{k=0}^{\infty }\frac{{\left(-i\frac{t}{\hslash }\right)}^k}{k!}\sum _n{c}_n{\hat{H}}^k{\psi }_n(\mathbf{r})\\ & =\sum _{k=0}^{\infty }\frac{{\left(-i\frac{t}{\hslash }\right)}^k}{k!}\sum _n{c}_n(E_n{)}^k{\psi }_n(\mathbf{r})\\ & =\sum _{k=0}^{\infty }\frac{{\left(-i\frac{t}{\hslash }\right)}^k}{k!}(E_n{)}^k\sum _n{c}_n{\psi }_n(\mathbf{r})\\ & =e^{-i\frac{E_n}{\hslash }t}\sum _n{c}_n{\psi }_n(\mathbf{r})\\ & =\sum _n{c}_n{\psi }_n(\mathbf{r})e^{-i\frac{E_n}{\hslash }t}\end{array}$

\qquad
主要参考书籍：
[1] Griffiths. 量子力学概论
[2] 钱伯初. 量子力学
[3] 周世勋. 量子力学教程