2-GMM-HMMs语音识别系统-训练篇

本文记录在传统的语音识别中，训练GMM-HMMs声学模型过程中的公式推导过程。

Outline

1. GMM - 混合高斯模型
2. HMM – 隐马尔科夫模型
3. Forward-Backward Algorithm – 前向后向算法

首先假设这里的训练数据，都做好了音素层面标记的（Label），即utterance的音素边界是已知的。这样做是为了更好地说明和对应我们的HMM建模单元（monophone）。后面会介绍Embedded Training，训练数据只需要语音+对应utterance的标记就行了。

1.GMM - 混合高斯模型

GMM表达式：

bj(x)=p(x)=∑m=1McjmN(x;μjm,Σjm)(1)

N(x;μjm,Σjm)=1(2π)D2|Σjm|12exp(−12(x−μjm)TΣ−1jm(x−μjm))(2)

x 代表一帧语音对应的特征参数值， cjm , μjm , Σjm 分别为为第 j 个状态的第 m 个高斯的混合系数（mixing parameters），均值（mean），方差（variance）, bj(x) 则为语音特征参数 x 属于状态 j 的概率。混合高斯模型，类似k均值聚类（k-means clustering）算法，属于一种迭代软聚类（soft clustering）算法。理论上，混合高斯模型能够表示特征空间上任何概率分布。混合高斯模型的参数可以通过EM算法训练得到，分Expectation-step、Maximization-step。

2.HMM – 隐马尔科夫模型

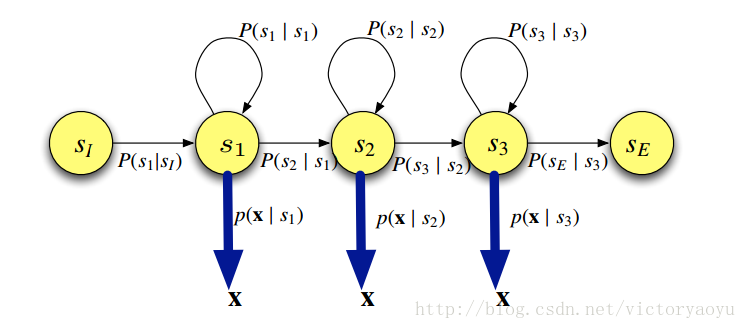
隐马尔科夫模型，是在马尔科夫链（Markov chain）的基础上，增加了观测事件（observed events）；即把马尔科夫链原本可见的状态序列隐藏起来，通过一个可观测的显层来推断隐层的状态信息。其中，隐层映射到显层通过发射概率（emission probability）或观测概率（observation probability）来计算，隐层状态之间的转移通过转移概率（transition probability）获得。下图是一个HMM结构：

这也是在语音识别中常用的一种隐马尔科夫模型结构，也称为Bakis模型。一般我们对每一个音素建立一个HMM，其中包括三个emitting state，一个start state（non-emitting ）和一个end state（non-emitting ）。HMM的数学形式为：

Q=q1q2⋯qN状态集合A=a11a12⋯an1⋯ann转移矩阵AO=o1o2⋯oN观测序列B=bi(ot)观测矩阵q0,qT开始状态，终止状态

所以，对于一个**给定结构的**HMM，我们需要通过训练获得它的A、B矩阵，即求解emission probability和transition probability。而在GMM-HMMs中，GMM作为HMM中的 bj(ot) ，即发射概率。下节则具体列出GMM-HMMs的推导公式。

3.Forward-Backward Algorithm – 前向后向算法

（一大波公式来袭！）

在GMM-HMMs的传统语音识别中，GMM决定了隐马尔科夫模型中状态与输入语音帧之间的符合情况，和HMM用来处理在时间轴上的声学可变性（自跳转）。训练HMM需要用到Forward-backward算法（Baum-Welch算法），本质上是一种EM算法。

 
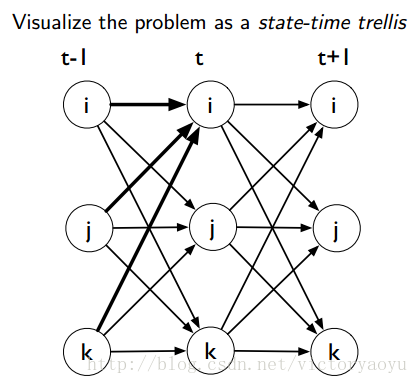
图为部分的状态-时间篱笆网络，为方便理解下面前向、后向概率。

3.1前向概率（The Forward Probability）

前向概率 αt(j) 代表 t 时刻处于状态 i ，且之前的观测序列为 x1,⋯,xt 的概率，即 

αt(j)=p(x1,⋯,xt,S(t)=j|λ)

1.α0(sI)=1;α0(j)=0,j≠sI2.αt(j)=[∑i=1Nαt−1aij]bj(xt),1≤j≤N,1≤t≤T3.p(X|λ)=αT(sE)=∑i=1NαT(i)aiE

注： sI =initial state,  sE =final state

3.2后向概率（The Backward Probability）

后向概率 βt(j) 是 已知 t 时刻处于状态 j ，输出之后的观测序列为 xt+1,⋯,xT 的概率，即 

βt(j)=p(xt+1,⋯xT|S(t)=j,λ)

1.βT(i)=aiE2.βt(j)=∑j=1Naijbj(xt+1)βt+1(j),t=T−1,⋯,13.p(X|λ)=β0(I)=∑j=1NaIjbj(x1)β1(j)

3.3EM algorithm for single-Gaussian /HMM

EM算法训练single Gaussian-HMMs，在E-step计算Q函数中固定的数据依赖参数 γt(j) (for GMM), ξt(i,j) (for HMM transition)；在M-step更新GMM，HMM模型参数。这里可能有点misnomer，因为这里并没有很明显的体现出expectation maximization的过程，是因为前人已经帮你计算出来了。具体怎么确定依赖参数，和如何重估出模型参数，可参看上一篇博客《EM算法和Baum Welch算法》。本文直接给出过程结果。

首先给出在E-step需要计算的依赖参数，状态占用概率（The State Occupation Probability） γt(j) 是在给定观测序列 X 和模型参数 λ 下，在时刻 t 处于状态 j 的概率。

γt(j)=p(S(t)=j|X,λ)(S(t)=j|X,λ)=p(X,S(t)=j|λ)p(X|λ)=1αT(sE)αt(j)βt(j)

和 ξt(i,j) 是在给定观测序列 X 和模型参数 λ 下，在时刻 t 处于状态 j ，时刻 t+1 处于状态 j 的概率

ξ(i,j)=p(S(t)=1,S(t+1)=j|X,λ)=p(S(t)=1,S(t+1)=j,X|λ)p(X|λ)=αt(i)aijbj(xt+1)βt+1(j)αT(sE)

然后，EM算法的整体过程为选定一个flat-start（训练数据的均值、方差作为GMM初始均值和方差）或者K-means，和将HMM的forward和self-loop初始概率设置为0.75、0.25。具体如下： 
E-step:

For all time-state pairs 
1. 递归计算前向、后向概率： αt(j) , βt(j)  
2. 计算the State Occupation Probability  γt(j,m) 和 ξt(i,j)

M-step:

基于 γt(j) 和 ξt(i,j) ，重估single-Gaussian/HMM的均值、方差和转移概率：

μj^=∑Tt=1γt(j)xt∑Tt=1γt(j)Σj^=∑T=1γt(j)(xt−μj^)(xt−μj^)T∑Tt=1γt(j)aij^=∑Tt=1ξt(i,j)∑Nk=1∑Tt=1ξt(i,k)

3.4EM algorithm for Gaussian Mixture Model/HMM

进一步拓展到语料库（a corpus of utterances ），GMM作为HMM观测PDF。

E-step:

for all time-state pairs 
1. 递归计算前向、后向概率： αrt(j) , βrt(j)  
2. 计算the component-state occupation probabilities  γrt(j,m) 和 ξrt(i,j)

γrt(j,m)=1αT(sE)∑i=1Nαrt(j)aijcjmbjm(xt)βrt(j)ξrt(i,j)=p(S(t)=1,S(t+1)=j|X,λ)=αrt(i)aijbj(xt+1)βrt+1(j)αT(sE)

M-step:

基于 γrt(j,m) 和 ξrt(i,j) ，重估GMM/HMMs的均值、方差、混合系数和转移概率： 

μjm^=∑Rr=1∑Tt=1γrt(j,m)xrt∑Rr=1∑Tt=1∑Mm′=1γrt(j,m′)Σjm^=∑Rr=1∑Tt=1γrt(j,m)(xrt−μim^)(xrt−μjm^)T∑Rr=1∑Tt=1∑Mm′=1γrt(j,m′)cjm^=∑Rr=1∑Tt=1γrt(j,m)∑Rr=1∑Tt=1∑Mm′=1γrt(j,m′)aij^=∑Rr=1∑Tt=1ξrt(i,j)∑Rr=1∑Nk=1∑Tt=1ξrt(i,k)

这样迭代至收敛，就得到GMM-HMMs所有参数了。当然，如果我们建模单元是Triphone（三音素），那么就需要进行一系列优化，以解决训练数据稀疏性问题。