数据结构 —— 红黑树：定义、性质、节点插入操作

1、红黑树的定义

R-B Tree，全称是Red-Black Tree，又称为“红黑树”，它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是 红(Red) 或 黑(Black)。

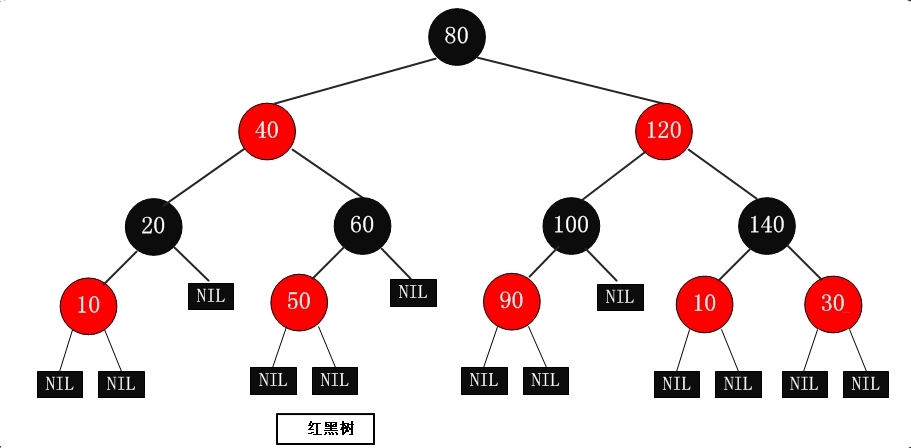
1.1、红黑树的性质

红黑树是一种含有红、黑结点，并能自平衡的二叉查找树，其性质如下：

1、每个结点或是红色的，或是黑色的
2、根节点是黑色的
3、每个叶结点（NIL）是黑色的
4、如果一个节点是红色的，则它的两个儿子都是黑色的。
5、对于每个结点，从该结点到其叶子结点构成的所有路径上的黑结点个数相同。

注意：

• 特性(3)中的叶子节点，是只为空(NIL或null)的节点。
• 特性(5)，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。

1.2、和AVL树的比较

AVL树是一棵严格的平衡树，它所有的子树都满足二叉平衡树的定义。因此AVL树高被严格控制在XXX，因此AVL树的查找比较高效。但AVL树插入、删除结点后旋转的次数比红黑树多。

红黑树用非严格的平衡来降低插入删除时旋转的次数。

因此，如果你的业务中查找远远多于插入、删除，那选AVL树；
如果查找、插入、删除频率差不多，那么选择红黑树。

1.3、红黑树的应用

红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。
例如，Java集合中的TreeSet和TreeMap，C++ STL中的set、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。

3、插入过程

为什么红黑树的默认插入结点为红色？
因为红黑树中黑节点至少是红节点的两倍，因此插入节点的父节点为黑色的概率较大，而此时并不需要作任何调整，因此效率较高。

3.1、空树时，红变黑

3.2、父为黑，直接插入

插入后无需任何操作。

由于黑节点个数至少为红节点的两倍，因此父为黑的情况较多，而这种情况在插入后无需任何调整，这就是红黑树比AVL树插入效率高的原因！

当父为红时，插入新节点也为红时，破坏了红黑树的性质，此时需要根据叔叔的颜色来做不同的处理，详见3.2、3.3

3.3、父为红，叔叔为红，则父叔同红，红加黑

父为红，叔叔为红时，只需交换爸爸、叔叔和爷爷的颜色即可。

此时，若爷爷节点和太爷爷节点颜色相同，再以爷爷节点为起始节点，进行刚才相同的操作，即：根据爷爷的兄弟颜色做相应的操作。

3.4、父为红，叔叔为黑或不存在，有4种情况

父为红，叔叔为黑时，颜色的变化是上中下，双黑加红。
分四种情况：

1）爸爸在左、叔叔在右、我在左时，则左旋，黑加红

以爸爸为根节点，进行一次右旋转； 颜色是双黑加红。

2）爸爸在左、叔叔在右、我在右时，则左右转，黑加红

先以我为根节点，进行一次左旋转；
再以我为根节点，进行一次右旋转。
颜色是双黑加红。

总结：

b情况比a情况多了一次左旋转，之后的操作与a相同。

---

上面的a、b是爸爸在左、叔叔在右、我在 左，
下面的c、d是叔叔在左、爸爸在右、我在 右 ，颜色变化是一样的，只是旋转方向正好相反。

---

3）叔叔在左、爸爸在右、我在右时，则左转，黑加红

以爸爸为根节点，进行一次左旋转。
颜色是双黑加红。

4）叔叔在左、爸爸在右、我在左时，则右左转，黑加红

先以我为根节点，进行一次右旋转；
再以我为根节点，进行一次左旋转。
颜色是双黑加红。

3.5、总结

当一个节点为红时，它要么有两个黑色子节点，要么没有任何节点。

3.6、练习

习题1：请画下图的插入节点的自平衡处理过程。

思考题1：黑结点可以同时包含一个红子结点和一个黑子结点吗？

3.7、相关文章推荐

https://www.jianshu.com/p/e136ec79235c （特别注意练习题）