codeforces 463C（对角线技巧）

题意：选取两个点，分别得到两个点对应的对角线上的值，要求两个点走的对角线不能相交，然后求两个点的对角线的值最大。

思路：

对于一个n * n，求一个点的左对角线和右对角线的技巧为：

对于a[i][j]这个点对应的左对角线上的横坐标+纵坐标都等于i + j,右对角线 的i - j + n 都相等。

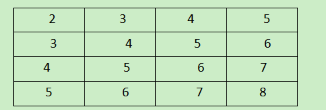
例如4 * 4 的：

i + j :为左对角线

i - j + n:右对角线

所以可用上面的下标统计左，右对角线元素的和，当统计一个点对应的对角线上的元素之和的时候，用左对角线上的值+右对角线上 - a[i][j].

PS：对于n *m的也适用。

这个题是统计两个点的对角线上的元素之和最大，并且不能相交，不能相交的话那么他们的i + j 不能奇偶性不能相同。

注意：d1,d2数组要开两倍大，一直wa就是因为这个情况。

#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define clr(x,y) memset(x,y,sizeof(x))
typedef long long ll;
const int maxn = 2000 + 10;

int n;
ll a[maxn][maxn];
ll d1[maxn * 2],d2[maxn * 2];

int main()
{
    while(  ~ scanf("%d",&n))
    {
        clr(d1,0);clr(d2,0);
        int ans = 0;
        int x1 = 0,y1 = 0,x2 = 0,y2 = 0;
        ll temp1 = 0,temp2 = 0;
        for(int i = 1; i <= n; i ++)
        {
            for(int j = 1; j <= n; j ++)
            {
                scanf("%I64d",&a[i][j]);
                d1[i + j] += a[i][j];d2[i - j + n] += a[i][j];
            }
        }
        for(int i = 1; i <= n; i ++)
        {
            for(int j = 1; j <= n; j ++)
            {
                ll t = d1[i + j] + d2[i - j + n] - a[i][j];
                if((i + j) & 1)
                {
                    if(temp1 <= t)temp1 = t,x1 = i,y1 = j;
                }
                else
                    if(temp2 <= t)temp2 = t,x2 = i,y2 = j;
            }
        }
        printf("%I64d\n%d %d %d %d\n",temp1 + temp2,x1,y1,x2,y2);
    }
    return 0;
}