All of Statistics 第二章

安仔都有人用

已于 2023-10-15 21:13:11 修改

阅读量288

点赞数 4

分类专栏：机器学习之统计学文章标签：随机变量 CDF PDF 二维CDF 多维CDF 二维分布边缘分布

于 2023-09-15 16:16:24 首次发布

机器学习之统计学专栏收录该内容

5 篇文章 2 订阅

订阅专栏

统计学（二）随机变量(Random Variables)

更新历史	日期	内容
1	2023-9-19	更正:例子2.46的 $F_X(x)=1-e^{-x}$
2	2023-9-25	更正:无解函数，应为无界函数

本章内容

引言
分布函数和概率分布(Distribution Functions and Probability Functions)
一些重要的离散随机变量(Discrete Random Variables )
一些重要的连续随机变量(Continuous Random Variables)
二维分布(Bivariate Distributions )
边缘分布(Marginal Distributions )
独立随机变量
条件分布(Conditional Distributions )
多维分布(Multivariate Distributions)和独立同步分布(IID)
两个重要的多维分布
随机变量的转换
多个随机变量的转换

关键名词,存在部分词不达意的情况,因此将关键名词整理如下

1. 分布函数:Distribution Functions
2. 概率函数:Probability Functions
3. 离散随机变量:Discrete Random Variables
4. 连续随机变量:Continuous Random Variables
5. 二维分布:Bivariate Distributions
6. 边缘分布:Marginal Distributions
7. 条件分布:Conditional Distributions
8. 多维分布:Multivariate Distributions

9. 累积分布函数:cumulative distribution function

10. 标准化:normalized

11. 概率函数:Probability function

12. 概率质量函数:Probability mass function

13. 概率密度函数:Probability density funciton

14. 连续:continuous

15. 分位函数:quantile function

16. 第一四分位:first quartile

17. 第二四分位:second quartile

18. 第三四分位:third quartile

19. 中位数:median

20. 等概率分布:equal in distribution

21. 点质量分布: Point Mass Distribution

22. 离散均匀分布:Discrete Uniform Distribution

23. 伯努利分布:Bernuolli Distribution

24. 二项分布:Binomial Distribution

25. 几何分布:Geometric Distribution

26. 泊松分布:Possion Distribution

27. 正态分布:Normal Distribution

28. 高斯分布:Gaussian Distribution

29. 标准正态分布:Standard Normal Distribution

30. 指数分布:Exponential Distribution

31. 伽马分布:Gamma Distribution

32. 贝塔分布:Beta Distribution

33. 柯西分布:Cauchy Distribution

34. 边缘分布:Marginal Distributions

35. 边缘质量函数:marginal mass function

36. 边缘密度函数:marginal denstiy function

37. 条件概率质量函数:Conditional Probability mass function

38. 条件概率密度函数:Conditional Probability Density funciton

40. 随机向量:Random Vector

41. 多项分布:Multinomial Distribution

42. 多元正态分布或者多维正态分布:Multivariate Normal

2.1 引言

统计学和数据挖掘关心的是数据,那么我们怎样将样本空间(sample)和事件(events)同数据联系起来呢?这种联系由随机变量(random variables)提供

2.1 随机变量(random variables)的定义

随机变量是一种映射,表示为 $X: \Omega \rightarrow \mathbb{R}$ ,即对于每一个结果ω,都有一个实数被分配给X(ω).

在概率课程的某些阶段,我们很少再提及样本空间(sapmle space),而是直接使用随机变量(random variables).但你应该牢记,样本空间(sample space)实际是存在,它隐含在随机变量的背后.

2.2 例子

抛硬币十次,令X(ω)是序列ω中正面朝上的个数,例如,ω=HHTHHTHHTT,那么X(ω)=6.

2.3 例子

设 $\Omega =\left \{ (x,y); x^{2} + y^{2} \leqslant 1\right \}$ 是一个单位圆,在Ω中随机取一点(我们将在后面更精确的描述这个想法),通常格式为ω=(x,y).那么随机变量的一些例子有:X(ω) = x,Y(ω) = y,Z(ω) = x+y或者 $W(\omega )=\sqrt{x^{2}+y^{2}}$

给定一个随机变量X和实数的子集A,定义 $X^{-1}(A)=\left \{ \omega \in \Omega : X(\omega) \in A \right \}$ 并令

$\mathbb{P}(X\in A) = \mathbb{P}(X^{-1}(A))=\mathbb{P}(\left \{ \omega \in \Omega; X(\omega) \in A \right \})$

$\mathbb{P}(X=x)=\mathbb{P}(X^{-1}(A))=\mathbb{P}(\left \{\omega \in \Omega;X(\omega)=x\right \})$

注意:X是随机变量,x是随机变量X的具体值

2.4 例子

抛硬币两次,令X为正面朝上的个数,那么P(X=0)=P({TT})=1/4, P(X=1)=P({HT,TH})=1/2 , P(X=2)=P({HH})=1/4,随机变量(random variables)和它的分布(distribution)可以总结如下:

ω	P({ω})	X(ω)
TT	1/4	0
TH	1/4	1
HT	1/4	1
HH	1/4	2

x	P(X=x)
0	1/4
1	1/2
2	1/2

2.2 分布函数(distribution functions)和概率函数(Probability functions)

给定一个随机变量X,我们按照如下的方式,定义其累积分布函数(cumulative distribution function)或分布函数(distribution functions):

2.5 CDF定义

累积分布函数(cumulative distribution function)或者CDF, $F_{x}:\mathbb{R}\rightarrow [0,1]$ 被定义为

$F_{X}(x)=P(X\leqslant x)$

在后面,我们将会看到CDF有效地包含了所有关于随机变量的信息.有时我们用 $F$ 代替 $F_{x}$ .

2.6 例子

扔一枚硬币两次,设X是正面朝上的次数.那么 $\mathbb{P}(X=0)=\frac{1}{4},\mathbb{P}(X=1)=\frac{1}{2},\mathbb{P}(X=2)=\frac{1}{4}$ ,则分布函数为:

$F_X(x)=\left\{\begin{matrix} 0 & ,x<0\\ \frac{1}{4} & ,0\leqslant x < 1\\ \frac{3}{4} & ,1 \leqslant x < 2\\ 1 & ,x \geqslant 2 \end{matrix}\right.$

则其对应的函数图形如下图

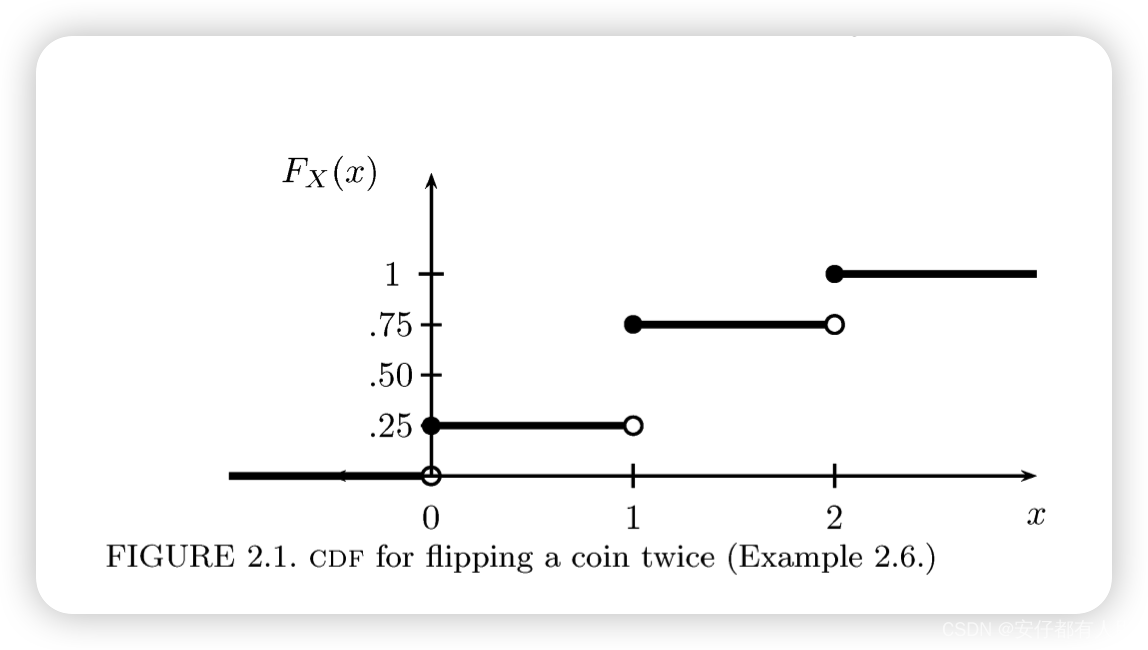
尽管这个例子非常简单,但是也请仔细的研究它,因为CDF的性质可能令人困惑.

注意,这个函数,是右连续,非递减,尽管x只取0,1,2但对所有的实数都有定义.你明白了为什么 $F_X(1.4)=.75$ 了吗?

以下的定理表明,CDF完全决定了随机变量(random variables)的分布

2.7 定理

设X有累积分布函数(CDF)F,Y有累积分布函数(CDF)G,如果对于所有的x,满足 $F(x)=G(x)$ ,那么对于所有的A,则有 $\mathbb{P}(X\in A) = \mathbb{P}(Y \in A)$

译者注:上面的定理可以看成CDF决定了概率分布

2.8 定理

F是[0,1]上的映射,当且仅当F满足下面三个条件的时候, F是某个概率P的累积分布函数.

F非递增:x1<x2,则F(x1) <= F(x2)
F已经标准化(normalized): $\lim_{x\rightarrow -\infty }F(x)=0$ , $\lim_{x\rightarrow \infty }F(x)=1$
F右连续:对于所有x, $F(x)=F(x^{+})$ ,其中 $F(x^+)=\lim_{\begin{matrix} y\to x\\ y\geq x \end{matrix}}F(y)$

证明:

假定F是CDF,让我们证明第三点成立.

设x是一个实数;

y1,y1,...是一个实数序列,满足y1>y2>...并且 $\lim_iy_i=x$ .

那么, $A_i=(-\infty,y_i],A=(-\infty,x]$

则得, $A= \bigcap_{i=1}^{\infty}Ai$ , $A1\supset A2\supset A3 ...$

所以, $\lim_iP(A_i)=P(\bigcap_iA_i)$

所以, $F(x)=P(A)=P(\bigcap_iA_i)=\lim_iP(A_i)=\lim_iF(y_i)=F(x^+)$

证毕

第一点和第二点类似.

证明另外一个方向------即,倘若F满足第一二三点,证明F是某个概率P的CDF-----需要使用分析领域更深层次的工具.

2.9 概率函数(Probability function)或概率质量函数(Probability mass function)定义

如果随机变量X取值有限,且离散.那么X的概率函数(probability function)或者概率质量函数(probability mass function)被定义为:

$f_X(x)=P(X=x)$ .

因此,对于所有的 $x\in R$ ,都有 $f_X(x) \geq 0$ ,且 $\sum_if(x_i)=1$ .有时我们直接用 $f$ 代替 $f_X$ .

CDF和 $f_X$ 的关系为:

$F_X(x)= P(X\leq x) = \sum_{x_i\leq x}f_X(xi)$

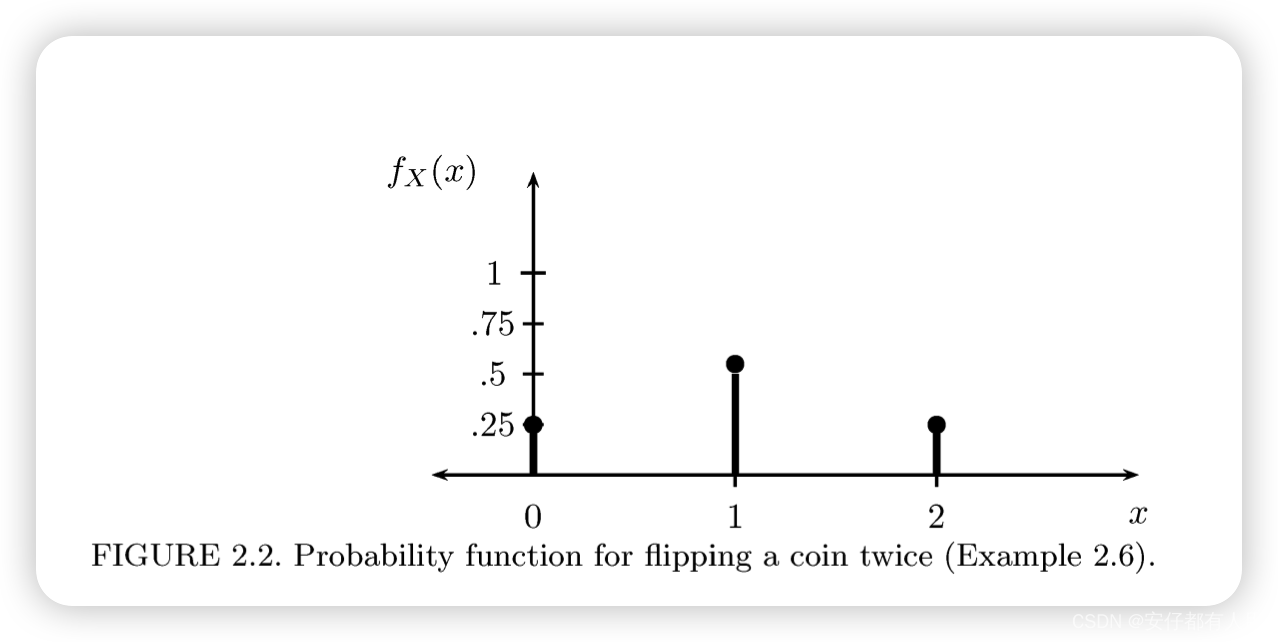
2.10 例子

2.6例子的概率函数(probability function)为

$f_X(x)=\left\{\begin{matrix} 1/4 & x=0 \\ 1/2 & x=1\\ 1/4& x=2 \\ 0 & otherwise \end{matrix}\right.$

见下图

2.11 概率密度函数(probability density function)定义

对于一个连续(continuous)的随机变量X,如果对于所有的x,存在一个函数 $f_X(x)$ 满足 $f_X(x)\geq 0$ , $\int_{-\infty}^{\infty}f_X(x)=1$ ,且满足, $a \leq b,\mathbb{P}(a < x <b)=\int_a^bf_X(x)dx$ ,那么就称 $f_X(x)$ 为概率密度函数(probability density function)PDF.

因此可以得 $F_X(x) = \int_{-\infty}^xf_X(x)dx$ 和 $f_X(x)={F}'_X(x)$ ,其中在所有x点处, $F_X$ 都是可导的.

有时,我们用 $\int f(x)dx$ 或者 $\int f$ 来表示 $\int_{-\infty}^\infty f(x)dx$

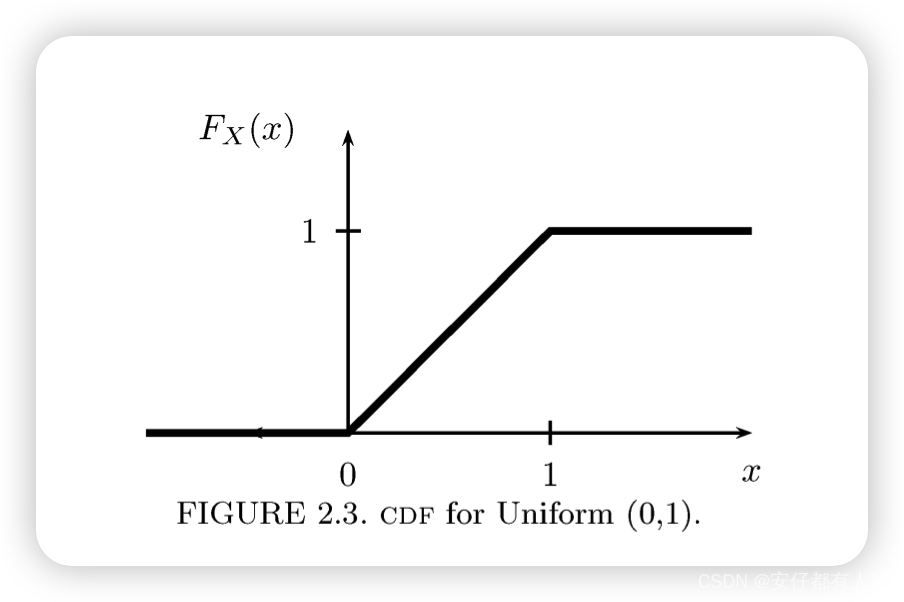
2.12 例子

设随机变量X的概率密度函数PDF,如下

$f_X(x)=\left\{\begin{matrix} 1 & for 0 \leq x \leq 1 \\ 0 & otherwise \end{matrix}\right.$

显然, $f_X(x)\geq 0$ 且 $\int f_X(x)dx=1$ .那么带有这种PDF的随机变量被称为 Uniform(0,1) 分布.Uniform(0,1)分布的概念表示,在[0,1]区间中随机选择一个点.

那么CDF,就为:

$F_X(x)=\left\{\begin{matrix} 0 & x <0 \\ x & 0 \leq x \leq 1\\ 1 & x > 1 \end{matrix}\right.$

如下图:

2.13 例子

假如随机变量X,有下面的PDF:

$f(x)=\left\{\begin{matrix} 0 & for x < 0\\ \frac{1}{(1+x)^2} & otherwise \end{matrix}\right.$

因为 $\int f(x)dx=1$ ,这是一个满足定义的PDF

警告;连续随机变量可能带来困惑.

首先应注意,如果X是连续的,那么对于任意x,都有 $\mathbb{P}(X=x)=0$ 不要尝试将 $f(x)$ 当做 $\mathbb{P}(X=x)$ ,这个只对离散随机变量有效. 连续随机变量对应的概率是通过PDF的积分得到.

其次还要注意,PDF是可以大于1的(这个跟概率质量函数(probability mass function)不同),例如:

$f(x)=\left\{\begin{matrix} 5 & x \in [0,1/5]\\ 0 & otherwise \end{matrix}\right.$ 可得, $f(x) \geq 0$ 且 $\int f(x)dx =1$ ,因此其是一个满足定义的PDF,但其在某些区间可得f(x)=5.事实上,PDF,可以是无界的,例如: $f(x)=\left\{\begin{matrix} \frac{2}{3}x^{-\frac{1}{3}} & 0 < x < 1\\ 0 & otherwise \end{matrix}\right.$ ,可得 $\int f(x)dx =1$ ,因此也是一个符合定义的PDF,但是它是无界函数.

2.14 例子

设 $f(x)=\left\{\begin{matrix} 0 & x < 0 \\ \frac{1}{(1+x)} & otherwise \end{matrix}\right.$ ,这个不是一个PDF,因为:

$\int f(x)dx=\int_0^\infty dx/(1+x)=\int_1^\infty du/u = log(\infty) = \infty$

2.15 引理

设F是随机变量X的CDF,那么:

$\mathbb{P}(X=x)=F(x)-F(x^-),where F(x^-)=\lim_{y \to x}F(y)$
$\mathbb{P}(x < X \leq y) =F(y) -F(x)$
$\mathbb{P}(X > x) = 1- F(x)$
如果X是连续的,那么 $F(b)-F(a)= \mathbb{P}(a < X < b) = \mathbb{P}(a \leq X < b)=\mathbb{P}(a < X \leq b)=\mathbb{p}(a \leq X \leq b)$

这对于定义CDF的逆函数(或者分位函数(quantile function))是有用的.

2.16 CDF的逆函数或者分位函数的定义

设X是一个有累积分布函数F的随机变量.那么CDF的逆函数或者分位函数(quantile function)被定义为:

$F^{-1}(q)=inf\left \{ x:F(x) > q \right \}$ ,其中 $q \in [0,1]$ ,

如果F是严格递增且连续,那么 $F^{-1}(q)$ 有唯一的实数x,使得 $F(x)=q$

我们将 $F^{-1}(1/4)$ 称为:第一四分位(first quartile) ;将 $F^{-1}(1/2)$ 称为:中位数(median)或者第二四分位(second quartile);将 $F^{-1}(3/4)$ 称为:第三四分位(third quartile)

两个随机变量X和Y,它们是等概率分布(equal in distribution),则可以写成 $X \overset{\text{d}}{=} Y$ .如果对于所有的x,都有 $F_X(x)=F_Y(x)$ ,这并不意味着X和Y是相等的.它只意味着X和Y有相同的概率状态.例如,设 $\mathbb{P}(X=1)=\mathbb{P}(X=-1)=1/2$ ,令Y=-X,则得 $\mathbb{P}(Y=1)=\mathbb{P}(Y=-1)=1/2$ ,所以 $X \overset{d}{=} Y$ ,但X和Y是不相等的.事实上 $\mathbb{P}(X=Y)=0$

2.3 一些重要的离散随机变量

关于符号的警告: $X \sim F$ 表示随机变量X的概率分布函数为F,这中传统的写法,并不合适,因为这个~符号也用来表示近似.符号 $X \sim F$ 太根深蒂固,以至于我们不得不沿用它.当我们看到这个符号的时候,应该将它当做:随机变量X满足分布F,而不是当做,X近似于F

Point Mass Distribution(点质量分布):如果概率满足下面的条件,那么随机变量X在a处有一个 Point Mass Distribution,写作 $X \sim \delta_a$ ,:

$\mathbb{P}(X=a)=1$ ,

那么 $F(x)=\left\{\begin{matrix} 0 & x < a\\ 1 & x \geq a \end{matrix}\right.$ ,概率质量函数(probability mass function)则为

$f(x)=\left\{\begin{matrix} 1 & x = a\\ 0 & otherwise \end{matrix}\right.$

Discrete Uniform Distribution(离散均匀分布):设k>1是一个整数,假定X有如下的概率质量函数(probability mass function):

$f(x)=\left\{\begin{matrix} 1/k & x=1,2,...k\\ 0 & otherwise \end{matrix}\right.$

那么我们就说X有一个在{1,...k}上的均匀分布

Bernuolli Distribution(伯努利分布):令X代表一次硬币的抛掷,那么P(X=1)=p,P(X=0)=1-p,其中p在[0,1]之间,我们就说X具有伯努利分布(Bernoulli Distributtion),写作 $X\sim Bernoulli(p)$ .则其概率函数 $f(x)=P^x(1-p)^{1-x},x \in \left \{ 0,1 \right \}$

Binomial Distribution(二项分布):假定硬币正面朝上的概率为p, $0 \leq p \leq 1$ .抛硬币n次,令X为正面朝上的次数,假设每次抛掷是独立的,令 $f(x)=\mathbb{P}(X=x)$ 是其质量函数(mass function),则其展开如下:

$f(x)=\left\{\begin{matrix} \binom{n}{x}p^x(1-p)^{n-x} & x=0,...n\\ 0 & otherwise \end{matrix}\right.$

有这种质量函数的随机变量,我们称之为二项随机变量,写作 $X\sim Binomial(n,p)$ .如果 $X_1\sim Binomial(n_1,p), X_2 \sim Binomial(n_2,p)$ ,那么 $X_1 + X_2 \sim Binomial(x_1+x_2,p)$

警告:让我们借此机会来防止一些易混淆点. X表示随机变量,x表示随机变量的具体取值;n和p是参数,即,固定的实数.参数p通常未知,必须从数据中得到,这也是统计推断的内容.在大多数统计模型中,同时存在随机变量和参数,不要将他们混淆了.

Geometirc Distribution(几何分布):如果X有如下的概率函数,则随机变量X服从参数为p的几何分布(geometric distribution),写作 $X \sim Geom(p)$ :

$\mathbb{P}(X=k)=p(1-p)^{k-1},k \geq 1$

我们可得:

$\sum_{k=1}^{\infty}P(X=k)= p\sum_{k=1}^{\infty}(1-p)^k=\frac{p}{1-(1-p)}=1$

将X视为抛硬币时,第一次出现正面所需的次数.

Possion Distribution(泊松分布):如果概率质量函数如下,则随机变量X服从参数为λ的泊松分布.写作: $X\sim Poisson( \lambda )$ :

$f(x)=e^{- \lambda } \frac{\lambda ^ x}{x!}, x \geq 0$

注意:

$\sum_{x=0}^{\infty}f(x)=e^{-\lambda}\sum_{x=0}^{\infty}\frac{\lambda^x}{x!}=e^{-\lambda}e^{\lambda}=1$

泊松分布经常用来作为稀有事件的模型,如辐射衰减,交通事故.如果 $X_1 \sim Poisson(\lambda_1),X_2 \sim Poisson(\lambda_2)$ 那么 $X_1+X_2 \sim Poisson(\lambda_1+\lambda_2)$

警告:我们将随机变量定义为:一种从样本空间Ω到实数R上的一种映射,但在上面的分布中我们没有提及样本空间.正如我们早期提到过的,样本空间经常"消失",但它依然存在于背后.让我们来显式的构建一个伯努利随机变量,令Ω=[0,1],并定义P满足P([a,b])=b-a,其中 0 <= a <= b <= 1.取p为[0,1]上的定值,定义:

$X(\omega )=\left\{\begin{matrix} 1 & \omega \leq p\\ 0 & \omega > p \end{matrix}\right.$

那么,P(X=1)=P(ω<=p)=P([0,p])=p且P(X=0)=1-p.因此X服从伯努利分布,写作 $X\sim Bernoulli(p)$ .我们不会为上面所有的分布都进行这样的操作.事实上,我们将随机变量视为随机数,但从形式上看,它是一种定义在样本空间中的映射.

2.4 一些重要的连续随机变量

Uniform Distribution(均匀分布):如果X有如下的概率密度函数,则X满足均匀分布,写作 $X \sim Uniform (a,b)$ :

$f(x)=\left\{\begin{matrix} \frac{1}{b-a} & x \in [a,b]\\ 0 & otherwise \end{matrix}\right.$

a<b时,分布函数则为:

$F(x)=\left\{\begin{matrix} 0 & x < a\\ \frac{x-a}{b-a} & x \in [a,b]\\ 1 & x>b \end{matrix}\right.$

Normal(Gaussian) Distribution(正态分布,或者高斯分布):如果概率密度函数满足如下,则X满足参数μ和σ的正态分布(Normal Distribution)

$f(x)=\frac{1}{\sigma \sqrt{2\pi}} exp\left \{ -\frac{1}{2\sigma^2}(x-\mu )^2 \right \}$

此处,μ 是实数R, σ > 0.

参数μ是分布的中心(或均值),σ是分布的离散程度(或标准差).(均值和标准差将会在下一章进行定义).正态分布在概率论和统计学中扮演了重要的角色.自然界中的许多现象也近似于正态分布.在后面我们会学习中心极限定理(Center Limit Theorem),该定理表明,随机变量之和的分布可以近似于正态分布.

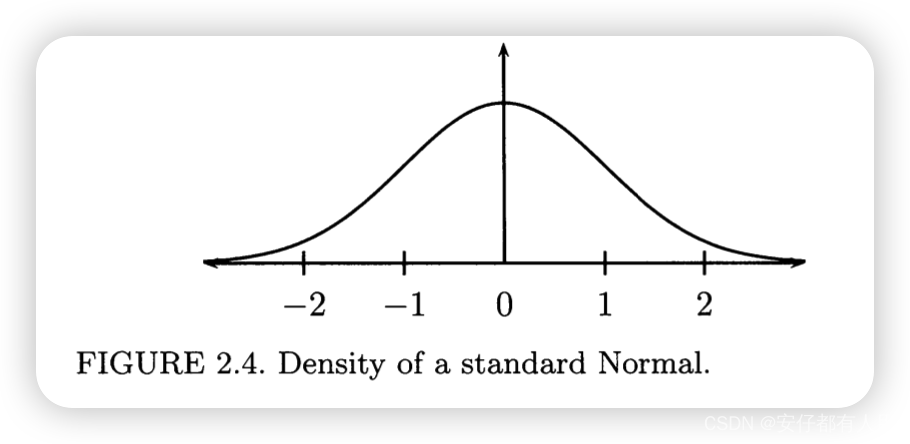
如果μ=0,σ=1,则称之为标准正态分布(standard Normal distribution).传统规定,标准正太随机变量用Z表示,而其PDF和CDF用 $\phi (z)$ 和 $\Phi (z)$ 表示.PDF图像如下:

下面给出一些有用的结论:

如果 $X\sim N(\mu,\sigma^2)$ ,那么 $Z=(X-\mu)/\sigma \sim N(0,1)$
如果 $Z \sim N(0,1)$ ,那么 $X=\mu+\sigma Z \sim N(\mu,\sigma ^2)$
如果 $X_i \sim N(\mu_i,\sigma_i^2)$ ,i=1,...n是独立的,那么 $\overset{n}{\underset{i=1}\sum}X_i \sim N\left ( \overset{n}{\underset{i=1}\sum}\mu_i,\overset{n}{\underset{i=1}\sum}\sigma_i^2 \right )$

从1可以推到出:

$P(a < x < b) =P(\frac{a-\mu}{\sigma} < Z < \frac{b-\mu}{\sigma}) = \Phi (\frac{b-\mu}{\sigma}) - \Phi(\frac{a-\mu}{\sigma})$

因此,只要我们可以计算标准正态的CDF,就可以计算任何概率.所有的统计计算包,都能计算 $\Phi(z)$ 和 $\Phi^{-1}(q)$ .大多数的统计学教材,包括本书,都有一个 $\Phi(z)$ 值表

2.17 例子

假定 $X \sim N(3,5)$ ,求 $\mathbb{P}(X>1)$ .解决思路是:

$\mathbb{P}(X>1) \\= 1- \mathbb{P}(X<1) \\= 1 - \mathbb{P}(Z<\frac{1-3}{\sqrt{5}})\\=1-\Phi(-0.8944)\\=0.81$

现在求 $q=\Phi^{-1}(0.2)$ ,这个意味着,我们需要求出q,满足P(X<q)=0.2.解决思路如下:

$0.2=P(X < q)\\=P(Z<\frac{q-\mu}{\sigma}) \\=\Phi(\frac{q-\mu}{\sigma})$

从标准表中, $\Phi(-0.8416)=0.2$ .因此, $-0.8416=\frac{1-\mu}{\sigma}=\frac{q-3}{\sqrt{5}}$ 得q=1.1181

Exponential Distribution(指数分布):如果概率密度函数满足如下,则X满足参数为β的指数分布(Exponential Distribution),写作: $X \sim Exp(\beta)$

$f(x)=\frac{1}{\beta}e^{-\frac{x}{\beta}},x>0,\beta > 0$

指数分布被用作建模电子元器件的生命周期,以及稀有事件之间的等待时间

Gamma Distribution(伽马分布):对于α>0,伽马函数(gamma function)定义为: $\Gamma(\alpha)=\int_0^\infty y^{\alpha-1} e^y dy$ .如果概率密度函数满足如下,则称X满足参数为α和β的伽马分布(gamma distribution),写作: $X\sim Gamma(\alpha,\beta)$

$f(x)=\frac{1}{\beta^\alpha \Gamma(\alpha)}x^{\alpha - 1}e^{-x/\beta},\alpha > 0,\beta > 0$

指数分布(Exponential Distribution)就是Gamma(1,β)分布.如果 $X_i\sim Gamma(\alpha_i,\beta)$ 是独立分布的,那么满足 $\sum_{i=1}^nX_i \sim Gamma(\sum_{i=1}^n \alpha_i,\beta)$

Beta Distribution(贝塔分布):如果f(x)满足如下条件,则X满足参数为α>0,β>0的贝塔分布(beta distribution),写作: $X \sim Beta(\alpha,\beta)$ :

$f(x)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1},0 < x <1$

t and Cauchy Distribution(t和柯西分布):如果f(x)满足如下条件,则称X满足自由度为v的t分布,写作: $X \sim t_v$ :

$f(x)=\frac{\Gamma(\frac{v+1}{2})}{\Gamma(\frac{v}{2})}\frac{1}{{(1+\frac{x^2}{v})}^{(v+1)/2}}$

t分布类似于正态分布,但其有更厚的尾部.事实上,正态分布对应于自由度v=∞的t分布 .而柯西分布则对应于v=1的t分布.概率密度函数为:

$f(x)=\frac{1}{\pi(1+x^2)}$

为了弄明白这确实是一个密度函数,对齐其积分得:

$\int_{-\infty}^\infty f(x) dx\\= \frac{1}{\pi}\int \frac{dx}{1+x^2} \\= \frac{1}{\pi}\int \frac{dtan^{-1}x}{dx}\\=\frac{1}{\pi}[tan^{-1}(\infty)-tan^{-1}(-\infty)]\\=\frac{1}{\pi}[\frac{\pi}{2}-(-\frac{\pi}{2})]=1$

$\chi ^2$ distribution(卡方分布):如果f(x)满足如下,则成X为自由度p个自由度的卡方分布(χ^2 distribution),写作: $X \sim \chi_p^2$

$f(x)=\frac{1}{\Gamma(p/2)2^{p/2}}x^{(p/2)-1}e^{-x/2},x>0$

如果Z1,Z2,...Zp是独立的标准正态随机变量,那么有 $\sum_{i=1}^p Z_i^2 \sim \chi_p^2$

2.5 二维分布(Bivariate Distributions)

给定一组离散的随机变量X和Y,定义联合质量函数(joint mass function)为: $f(x,y)=\mathbb{P}(X=x \ and\ Y = y)$ ,从现在开始,将 $\mathbb{P}(X=x \ and \ Y=y)$ 写成 $\mathbb{P}=(X=x,Y=y)$ .当需要更加复杂的式子时,将 $f_{x,y}$ 直接写成 $f$

2.18 例子

此处有两个随机变量X和Y的二维分布,他们的取值为0或1

	Y=0	Y=1
X=0	1/9	2/9	1/3
X=1	2/9	4/9	2/3
	1/3	2/3

因此,f(1,1)=P(X=1,Y=1)=4/9

2.19 二维随机变量的PDF定义

在连续情况下,如果满足下面三个条件,则称函数f(x,y)是变量(X,Y)的PDF

对于所有的 $(x,y)$ ,有 $f(x,y)\geq 0$
$\int_{-\infty}^\infty\int_{-\infty}^\infty f(x,y)dx dy = 1$ 并且
对于任意集合 $A \subset \mathbb{R} \times \mathbb{R}$ ,有 $\mathbb{P}((X,Y) \subset A)=\int\int_A f(x,y)dxdy$

在离散和连续的情况下,我们定义联合CDF为 $F_{X,Y}(x,y)=P(X\leq x,Y\leq y)$

2.20 例子

假设(X,Y)在单位正方形内是均匀的,那么有:

$f(x,y)=\left\{\begin{matrix} 1 & 0 \leq x \leq 1, 0\leq y \leq 1\\ 0 & otherwise \end{matrix}\right.$

求P(X<1/2,Y<1/2).

事件A={X<1/2,Y<1/2}对应于单位正方形的一个子集.在这种情况下,对f在这个子集上求积分.求出A的面积为1/4.所以P(X<1/2,Y<1/2)=1/4

2.21 例子

设(X,Y)有下面的概率密度函数:

$f(x,y)=\left\{\begin{matrix} x+y & 0 \leq x \leq 1, 0 \leq y \leq 1, \\ 0 & otherwise \end{matrix}\right.$

那么可得:

$\int_0^1 \int_0^1(x+y)dxdy\\\\=\int_0^1[\int_0^1xdx]dy+\int_0^1[\int_0^1ydx]dy\\\\=\int_0^1\frac{1}{2}dy+\int_0^1ydy\\\\=\frac{1}{2}+\frac{1}{2}=1$

此时,可证f(x,y)为PDF

2.22 例子

如果分布被定义在一个非矩形区域,那么计算将会有点复杂.此处有一个例子,引用至DeGroot and Schervish(2002).假设(X,Y)有下面的密度函数:

$f(x,y)=\left\{\begin{matrix} cx^2y & x^2 \leq y \leq 1 \\ 0& otherwise \end{matrix}\right.$

请注意, $-1 \leq x \leq 1$ .现在让我们来求c的值.

这里的关键是要注意积分得范围.我们选择一个变量，比如 x，然后让它在其取值范围内变化。然后，对于每个固定的 x 值，我们让 y 在其范围内变化，即 x^2 ≤ y ≤ 1。如果你查看下图,则可能会对你有所帮助

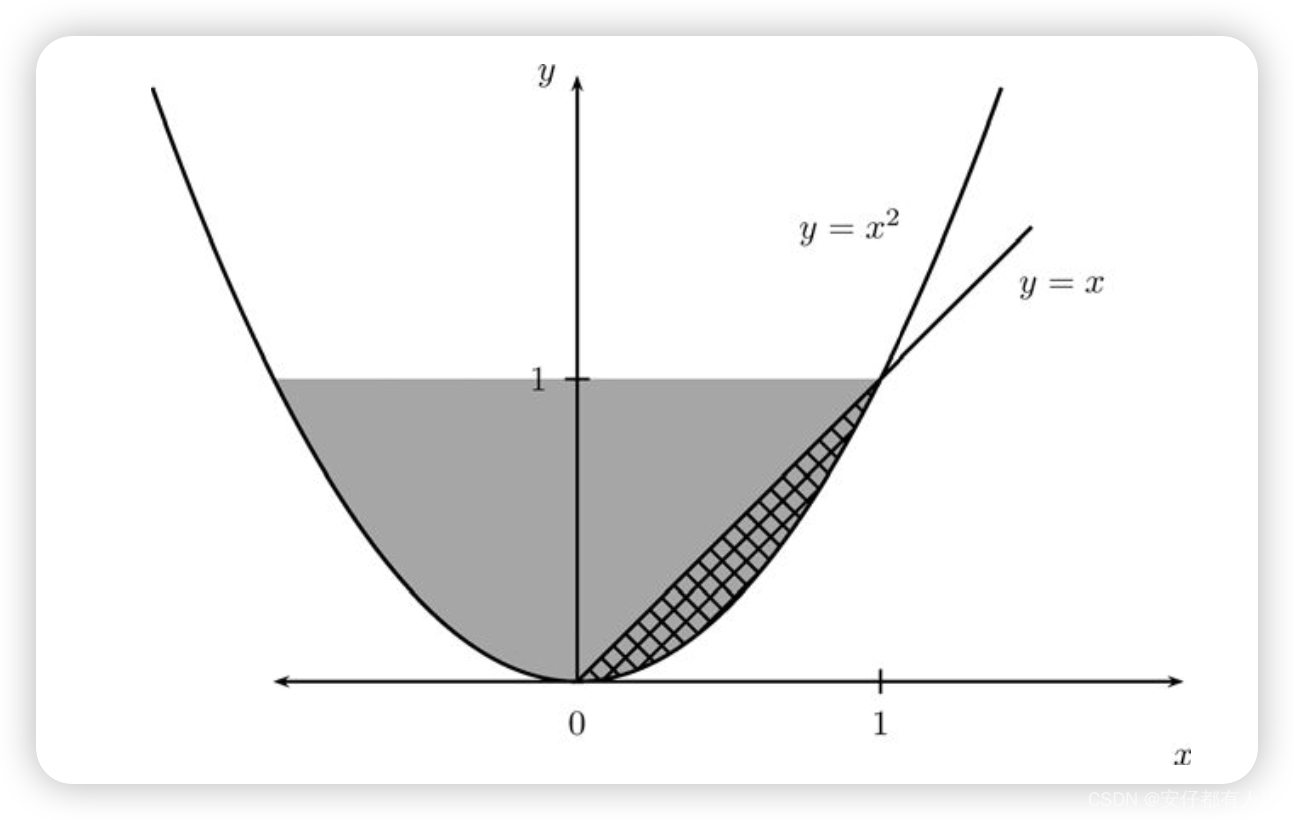
因此 $1 \\\\=\int\int f(x,y)dxdy = c \int_{-1}^1\int_{x^2}^1x^2ydydx\\\\=c\int_{-1}^1x^2[\int_{x^2}^1ydy]dx\\\\=c\int_{-1}^1x^2\frac{{1-x^4}}{2}dx\\\\=\frac{4c}{21}$ 因此c=21/4

现在让我们来计算P(X>=Y),这个对应的集合为:A={(x,y);0<=x<=1,x^2<=y<=x}因此

$\mathbb{P}(X\geq Y)=\frac{21}{4}\int_0^1\int_{x^2}^xydydx\\\\=\frac{21}{4}\int_0^1x^2[\int_{x^2}^xydy]dx\\\\=\frac{21}{4}\int_0^1x^2\frac{x^2-x^4}{2}dx\\\\=\frac{3}{20}$

2.6 边缘分布(Marginal Distributions)

2.23 定义

如果(X,Y)满足联合分布,且其质量函数为 $f_{x,y}$ .那么对于x的边缘质量函数(marginal mass function)被定义为:

$f_X(x)=P(X=x)=\underset{y}\sum P(X=x,Y=y)=\underset{y}\sum f(x,y)$

对于y的边缘质量函数(marginal mass function)被定义为:

$f_Y(y)=P(Y=y)=\underset{x}\sum P(X=x,Y=y)=\underset{x}\sum f(x,y)$

2.24 例子

假如 $f_{x,y}$ 由下表给出.对于X的边缘分布,则是行的总和,对于Y的边缘分布则是列的总和

	Y=0	Y=1
X=0	1/10	2/10	3/10
X=1	3/10	4/10	7/10
	4/10	6/10

可得 $f_X(0)=3/10$ , $f_X(1)=7/10$

2.25 定义

对于连续随机变量,边缘密度函数(marginal density function)被定义为:

$f_X(x)=\int f(x,y)dy , f_Y(y)=\int f(x,y)dx$

则对应的边缘分布函数,由 $F_X(x) and F_Y(y)$ 表示

2.26 例子

假定 $f_{X,Y}(x,y)=e^{-(x+y)}\ \ \ x,y\geq0$ ,那么 $f_X(x)=e^{-x}\int_0^\infty e^{-y}dy = e^{-x}$

2.27 例子

假如: $f(x,y)=\left\{\begin{matrix} x+y & 0 \leq x \leq 1,0 \leq y \leq 1\\ 0 & otherwise \end{matrix}\right.$ ,那么可得

$f_Y(y)=\int_0^1(x+y)dx=\int_0^1 xdx+\int_0^1ydx=\frac{1}{2}+y$

2.28 例子

令(X,Y)有如下的密度函数

$f(x,y)=\left\{\begin{matrix} \frac{21}{4}x^2y & x^2 \leq y \leq 1\\ 0 & otherwise \end{matrix}\right.$

因此,可得

$f_X(x)=\int f(x,y)dy = \frac{21}{4}x^2\int_{x^2}^1ydy=\frac{21}{8}x^2(1-x^4)$

2.7 独立随机变量 (Independent Random Variable)

2.29 定义

有两个随机变量X和Y,若对于所有A和B,有 $\mathbb{P}(X \in A,Y \in B)=\mathbb{P}(X \in A)\mathbb{P}(Y \in B)$ ,那么我们就说X和Y独立.写作 $X \coprod Y$ .反之,则称X和Y相关,写作,如下(贴图)

原则上,要检查X和Y是否独立,我们需要根据定义中的式子来检查所有的A,B子集.但幸运的是,我们有下面的结论可以使用,尽管这些结论是用连续的随机变量表述,但它也适用于离散随机变量

2.30 定理(Theorem)

假设X和Y有联合PDF $f_{x,y}$ ,当且仅当 $f_{X,Y}(x,y)=f_X(x)f_Y(y)$ 对于所有x和y成立时,那么 $X \coprod Y$

2.31 例子

设X,Y有下面的分布

	Y=0	Y=1
X=0	1/4	1/4	1/2
X=1	1/4	1/4	1/2
	1/2	1/2	1

那么 $f_X(0)=f_X(1)=1/2$ ,且 $f_Y(0)=f_Y(1)=1/2$ .X和Y是独立的,因为 $f_X(0)f_Y(0)=f(0,0)$ , $f_X(0)f_Y(1)=f(0,1)$ , $f_X(1)f_Y(0)=f(1,0)$ , $f_X(1)f_Y(1)=f(1,1)$ .

假如X,Y有下面的分布

	Y=0	Y=1
X=0	1/2	0	1/2
X=1	0	1/2	1/2
	1/2	1/2	1

那么X和Y不是独立的,因为 $f_X(0)f_Y(1)=1/4$ 但 $f(0,1)=0$

2.32 例子

假定X和Y是独立的,并且有相同的密度函数,如下:

$f(x)=\left\{\begin{matrix} 2x & 0 \leq x \leq 1\\ 0 & otherwise \end{matrix}\right.$ .

让我们来求 $\mathbb{P}(X+Y \leq 1)$ .使用独立性,那么联合密度函数就为:

$f(x,y)=f_X(x)f_Y(y)=\left\{\begin{matrix} 4xy & 0 \leq x \leq 1, 0\leq y\leq 1\\ 0 & ,otherwise \end{matrix}\right.$

得: $\mathbb{P}(X+Y \leq 1)\\\\=\int\int_{x+y \leq 1}f(x,y)dxdy\\\\=4 \int_0^1x[\int_0^{1-x}ydy]dx\\\\=4\int_0^1x\frac{(1-x)^2}{2}dx\\\\=\frac{1}{6}$

下面的结论有助于验证独立

2.33 定理

假定X和Y的范围是一个矩形(可能是无界的),如果对于函数g和h(不一定是概率密度函数),满足 $f(x,y)=g(x)h(y)$ ,那么X和Y是独立的.

2.34 例子

令X和Y有下面的密度函数:

$f(x,y)=\left\{\begin{matrix} 2e^{-(x+2y)} & ,x> 0,y>0 \\ 0 & ,otherwise \end{matrix}\right.$

X和Y的范围是一个矩形 $(0,\infty)\times (0 ,\infty)$ ,还可以将f(x,y)写成f(x,y)=g(x)h(y).其中, $g(x)=2e^{-x}$ , $h(y)=e^{-2y}$ .因此 $X \coprod Y$

2.8 条件分布(Conditional Distribution)

如果X和Y是离散的,那么我们可以计算在Y=y情况下的X的条件分布.具体来说 $\mathbb{P}(X=x|Y=y)=P(X=x,Y=y)/\mathbb{P}(Y=y)$ ,这使我们定义条件概率质量函数如下

2.35 条件概率质量函数(conditional probability mass function)定义

如果, $f_Y(y) > 0$ 条件概率质量函数定义如下:

$f_{X|Y}(x|y)=P(X=x|Y=y)=\frac{P(X=x,Y=y)}{P(Y=y)}=\frac{f_{X,Y}(x,y)}{f_Y(y)}$

对于连续分布,我们使用相同的定义.解释的不同则为:在离散情况下条件概率质量函数,就是条件概率 $f_{X|Y}(x|y)=P(X=x|Y=y)$ .而对于连续情况下,就必须进行积分求得概率.

2.36 条件概率密度函数(conditional probability density function)定义

对于连续的随机变量,条件概率密度函数(conditional probability density function)定义如下:假如 $f_Y(y)>0$ ,

$f_{X|Y}(x|y)=\frac{f_{X,Y}(x,y)}{f_Y(y)}$

那么,概率则为:

$P(X\in A | Y = y) = \int_A f_{X|Y}(x|y)dx$

2.37 例子

假设X和Y,在单位正方形上有一个联合均匀分布(joint uniform distribution).因此在 $0 \leq x \leq 1$ 下, $f_{X|Y}(x|y)=1$ .在其他地方则为0.给定Y=y的情况下,X就是Uniform(0,1)分布.我们可以写作: $X|Y=y \sim Uniform(0,1)$

从条件密度的定义可得: $f_{X,Y}(x,y)=f_{X|Y}(x|y)f_Y(y)=f_{Y|X}(y|x)f_X(x)$ .这在某些情况下非常有用,如2.39 例子

2.38 例子

设: $f(x,y)=\left\{\begin{matrix} x+y & 0 \leq x \leq 1 , 0 \leq y \leq 1\\ 0 & otherwise \end{matrix}\right.$ .求 $\mathbb{P}(X<1/4|Y=1/3)$

在2.27例子中,可得 $f_Y(y)=y+(1/2)$ .因此:

$f_{X|Y}(x|y)=\frac{f_{X,Y}(x,y)}{f_Y(y)}=\frac{x+y}{y+\frac{1}{2}}$

所以,

$\mathbb{P}(X<\frac{1}{4}|Y=\frac{1}{3})\\\\=\int_0^{1/4}f_{X|Y}(x|\frac{1}{3})dx\\\\=\int_0^{1/4}\frac{x+\frac{1}{3}}{\frac{1}{3}+\frac{1}{2}}dx\\\\=\frac{\frac{1}{32}+\frac{1}{12}}{\frac{1}{3}+\frac{1}{2}}\\\\=\frac{11}{80}$

2.39 例子

假如X服从 $X \sim Uniform(0,1)$ .在获得X值之后,产生的Y服从 $Y|X=x \sim Uniform(x,1)$ .那么Y的边缘分布函数是什么?

首先, $f_X(x)=\left\{\begin{matrix} 1 & ,0\leq x \leq 1\\ 0 & ,otherwise \end{matrix}\right.$ ,且 $f_{Y|X}(y|x)=\left\{\begin{matrix} \frac{1}{1-x} & , 0 < x< y< 1\\ 0 & ,otherwise \end{matrix}\right.$ 因此得

$f_{X,Y}(x,y)=f_{Y|X}(y|x)f_X(x)=\left\{\begin{matrix} \frac{1}{1-x} & ,0<x<y<1\\ o & ,otherwise \end{matrix}\right.$

则Y的边缘密度函数为:

$f_Y(y)=\int_0^y f_{X,Y}(x,y)dx=\int_0^y \frac{dx}{1-x}dx = - \int_1^{1-y}\frac{du}{u}=-log(1-y)$ ,其中 $0 < y<1$

2.40 例子

思考例子2.28中的密度函数,求 $f_{Y|X}(y|x)$ .

当X=x,y必须满足 $x^2 \leq y \leq 1$ .在前面,求出了 $f_X(x)=(21/8)x^2(1-x^4)$ .因此对于 $x^2 \leq y \leq 1$ ,则有:

$f_{Y|X}(y|x)=\frac{f(x,y)}{f_X{x}}=\frac{(21/4)x^2y}{(21/8)x^2(1-x^4)}=\frac{2y}{1-x^4}$

现在求 $\mathbb{P}(Y\geq 3/4 |X = 1/2)=\int_{3/4}^1f(y|1/2)dy=\int_{3/4}^1\frac{32y}{5}dy=\frac{7}{15}$

2.9 多维分布和独立同步分布(Multivariate Distributions And IID)

令X=(X1,X2...Xn),这里的X1,X2..Xn都是随机变量(Random Variables),称X为随机向量(Random Vector).令 $f(x_1,x_2,x_3.....x_n)$ 是其PDF.可以定义他们的边缘分布,条件分布,其大多于二维的情况类似.

如果对于每一个A1,A2,...An,有 $\mathbb{P}(X_1 \in A_1,X_2 \in A2....X_n \in A_n)= \overset{n}{\underset{i=1}{\prod}}\mathbb{P}(X_i \in A_i)$ ,则X1,X2...Xn是独立的.通过检查 $f(x_1,x_2,...x_n)=\overset{n}{\underset{i=1}{\prod }}f_{X_i}(x_i)$ 即可.

2.41 IID定义

如果X1,X2,....Xn相互独立的,且有相同的累积分布函数(CDF)F,我们就说X1,X2,...Xn是独立同步分布(independent and identically distributed)写作: $X_1,...X_n \sim F$ .

如果F的密度函数为f,也可以写作 $X_1,..X_n \sim f$ .我们也称X1,...Xn是来自于F的n个随机样本(random sample of size n from F)

统计学理论和实践的大部分内容都以独立同分布（IID）的观测数据为基础，当我们讨论统计学时，我们将详细研究这种情况。

2.10 两个重要的多维分布

Multinomial (多项分布):二项分布的多维版本就称为多维分布.考虑从装有k个不同颜色的盒子中,抽取1个小球.这些小球上标有:"color1,color2....colork".令p=(p1,...pk),其中pj>=0,且 $\sum_{j=1}^kp_j=1$ ,设pj是抽中小球颜色为j的概率.抽n次(有放回的独立抽样)且令X=(X1,X2..Xk)其中Xj表示颜色j出现的次数.因此 $n=\sum_{j=1}^kX_j$ .此时我们就说X满足Multinomial(n,p)分布,写作: $X \sim Multnomial(n,p)$ .对应的概率函数为:

$f(x)=\binom{n}{x_1...x_k}p_1^{x_1}...p_k^{x_k}$

其中, $\binom{n}{x_1...x_k}=\frac{n!}{x_1!...x_k!}$

2.42 引理

假如 $X \sim Multinomial(n,p)$ ,其中X=(X1,X2..Xk),p=(p1,p2...pk).Xj的边缘分布就是Binomial(n,pj)分布

Multivariate Normal(多维正态分布或者多元正态分布):一维正态分布有两个参数,μ和σ.在多维的版本中,μ是一个向量,σ则是一个矩阵Σ.

现在令

$Z=\begin{pmatrix} Z_1\\ \vdots \\ Z_k \end{pmatrix}$

其中, $Z_1...Z_k \sim N(0,1)$ 且相互独立.则Z的密度函数为:

$f(z)=\overset{k}{\underset{i}{\prod }}f(z_i)=\frac{1}{(2\pi)^{k/2}}exp\left \{ -\frac{1}{2} \overset{k}{\underset{i}{\sum}} z_j^2\right \}\\\\=\frac{1}{(2\pi)^{k/2}}exp\left \{ -\frac{1}{2}z^Tz \right \}$

我们就说Z符合标准的多元正态分布,写作: $Z\sim N(0,I)$ ,其中,0表示有k个0元素的向量. 大写的I表示 $k\times k$ 的单位矩阵.

更一般的,如果向量X有下面的密度函数,则X是一个多维的正态分布向量,记作: $X \sim N(\mu,\Sigma)$

$f(x;\mu,\Sigma)=\frac{1}{(2\pi)^{k/2}|(\Sigma)|^{1/2}}exp\left \{ -\frac{1}{2} (x-\mu)^T \Sigma^{-1}(x-\mu)\right \}$

其中 $|\Sigma|$ 表示Σ的行列式.μ是一个长度为k的向量.Σ是一个 $k\times k$ 对称的正定矩阵. 如果μ=0,Σ=I,则变成了标准多维正态分布

因为Σ是对称,正定矩阵.因此存在一个矩阵 $\Sigma^{1/2}$ ----称为Σ的平方根----满足下面的性质:

$\Sigma^{1/2}$ 也是对称的
$\Sigma=\Sigma^{1/2}\Sigma^{1/2}$
$\Sigma^{1/2}\Sigma^{-1/2}=\Sigma^{-1/2}\Sigma^{1/2}=I$ ,其中 $\Sigma^{-1/2}=(\Sigma^{1/2})^{-1}$

2.43 定理

如果 $Z \sim N(0,I)$ 并且 $X=\mu+\Sigma^{1/2}Z$ ,那么 $X\sim N(\mu,\Sigma)$ 反之,如果 $X \sim N(\mu,\Sigma)$ 那么 $\Sigma^{-1/2}(X-\mu) \sim N(0,I)$

假定将随机正态向量X分成X=(Xa,Xb)那么可以将μ写成μ=(μa,μb),Σ写成 $\Sigma=\begin{pmatrix} \Sigma_{aa} & \Sigma_{ab}\\ \Sigma_{ba} & \Sigma_{bb} \end{pmatrix}$

2.44 定理

设 $X \sim N(\mu,\Sigma)$ ,那么

Xa的边缘分布满足: $X_a \sim N(\mu_a,\Sigma_{aa})$
Xa=xa条件下的Xb的条件分布为: $X_b|X_a=x_a \sim N(\mu_b+\Sigma_{ba}\Sigma_{aa}^{-1}(x_a-\mu_a),\Sigma_{bb}-\Sigma_{ba}\Sigma_{aa}^{-1}\Sigma_{ab})$
如果a是一个向量,那么 $a^TX \sim N(a^T\mu,a^T\Sigma a)$
$V=(X-\mu)^T\Sigma^{-1}(X-\mu) \sim \chi _k^2$

2.11 随机变量的转换

假如X是CDF为 $F_X$ ,PDF为 $f_X$ 的随机变量.令 $Y=r(X)$ 是关于X的函数.例如 $Y=X^2$ ,或者 $Y=e^X$ .我们称 $Y=r(X)$ 为X的转换.那么我们怎么计算Y的PDF和CDF呢?在离散情况下,答案非常容易.Y的质量函数如下:

$f_Y(y)=\mathbb{P}(Y=y)=\mathbb{P}(r(X)=y)=\mathbb{P}(\left \{ x;r(x)=y \right \})\\\\=\mathbb{P}(X \in r^{-1}(y))$

2.45 例子

假如P(X=-1)=P(X=1)=1/4 ,P(X=0)=1/2.令Y=X^2.那么P(Y=0)=P(X=0)=1/2,P(Y=1)=P(X=1)+P(X=-1)=1/2.如下:

x	$f_X(x )$
-1	1/4
0	1/2
1	1/4

y	$f_Y(y)$
0	1/2
1	1/2

Y的取值比X的取值少,这是因为这种转换不是一对一的.

而对于连续情况就比较复杂了,这儿有下面三个步骤去求 $f_Y$

对于每一个y,找到集合 $A_y=\left \{ x;r(x) \leq y \right \}$
再求出CDF:

$F_Y(y)=P(Y\leq y)=P(r(X) \leq y)=P(\left \{ x;r(x) \leq y \right \})\\\\=\int_{A_y}f_X(x)dx$

3. PDF就为CDF的导数: $f_Y(y)={F_Y}'(y)$

2.46 例子

令 $f_X(x)=e^{-x}$ ,x>0.因此 $F_X(x)=\int_0^x f_X(s)ds= 1- e^{-x}$ .设 $Y=r(X)=logX$ .那么 $A_y=\left \{ x:x \leq e^y \right \}$ 那么

$F_Y(y)=P(Y \leq y)=P(logX \leq y)=P(X \leq e^y)=F_x(e^y)=1-e^{-{e^y}}$

因此 $f_Y(y)=e^ye^{-e^y},y \in \mathbb{R}$

2.47 例子

设 $X \sim Uniform(-1,3)$ ,求 $Y=X^2$ 的PDF.X的密度函数为:

$f_X(x)=\left\{\begin{matrix} 1/4 & , -1 < x< 3\\ 0 & ,otherwise \end{matrix}\right.$

Y仅可取(0,9)之间的值,考虑两种情况:第一种, 0<y<1 ;第二种, 1<= y < 9.

对于第一种情况, $A_y=[-\sqrt{y},\sqrt{y}]$ . $F_Y(y)=\int_{A_y}f_X(x)dx=(1/2)\sqrt{y}$

对于第二种情况, $A_y=[-1,\sqrt{y}]$ , $F_Y(y)=\int_{A_y}f_X(x)dx=(1/4)(\sqrt{y}+1)$

对F求导得:

$f_Y(y)=\left\{\begin{matrix} \frac{1}{4\sqrt{y}} &, 0 < y< 1\\ \frac{1}{8\sqrt{y}} & , 1<y<9\\ 0 & ,otherwise \end{matrix}\right.$

当r是严格的单调递增,或者单调递减,那么r有其反函数, $s=r^{-1}$ ,在这种情况密度函数可以表示为:

$f_Y(y)=f_X(s(y))|\frac{ds(y)}{dy}|$

2.12 多个随机变量的转换

在某些情况下,我们对多个随机变量的转换感兴趣.例如,如果X和Y是给定的随机变量.我们可能像知道X/Y,X+Y,max{X,Y}的分布.令Z=r(X,Y)为我们感兴趣的函数.那么求 $f_Z(z)$ 的步骤和前面的类似:

对于每一个z,找到集合 $A_z=\left \{ (x,y) :r(x,y) \leq z\right \}$
求出CDF:

$F_Z(z)=P(Z \leq z)=P(r(X,Y) \leq z)=P(\left \{ (x,y):r(x,y) \leq z \right \})\\\\=\int\int_{A_z}f_{X,Y}(x,y)dxdy$

3. 然后对其求导; $f_Z(z)={F_Z}'(z)$

2.48 例子

设 $X_1,X_1 \sim Unifrom(0,1)$ 且独立.求 $Y=X_1+X_2$ 的密度函数

(X1,X2)的联合密度函数为:

$f(x_1,x_2)=\left\{\begin{matrix} 1 &\ 0 \leq x \leq 1,0 \leq y \leq 1\\ 0 & otherwise \end{matrix}\right.$

令 $r(x_1,x_2)=x_1+x_2$ ,得:

$F_Y(y)=P(Y \leq y)=P(r(X_1,X_2) \leq y)=P(\left \{ (x_1,x_2);r(x_1,x_2) \leq y \right \}) \\\\=\int\int_{A_y}f(x_1,x_2)dx_1dx_2$

现在来到了困难的部分:求出 $A_y$ .

首先假设 $0 < y \leq 1$ ,那么 $A_y$ 就是(0,0),(y,0),(0,y)围成的三角形.如下图

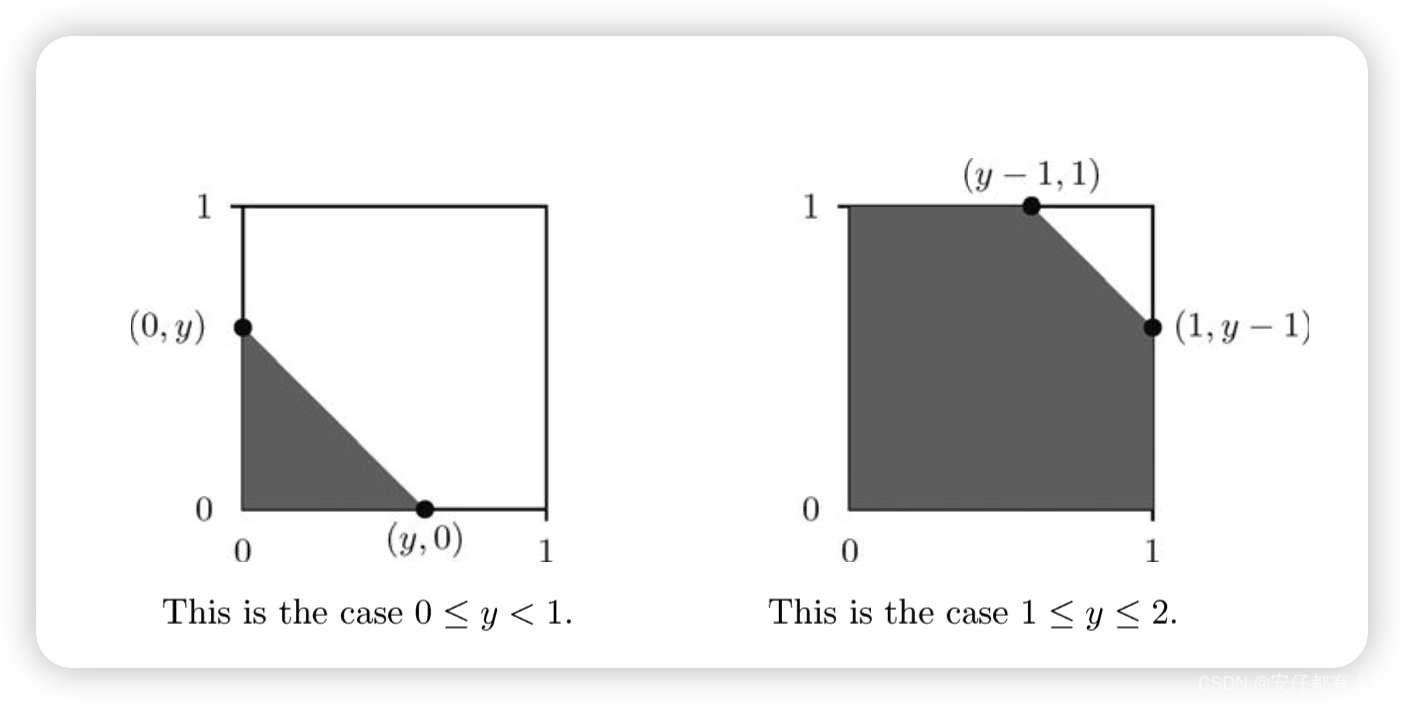
在此种情况下, $\int\int_{A_y}f(x_1,x_2)dx_1dx_2$ 是三角形的面积为 $y^2/2$

再假设 $1 < y< 2$ ,那么 $A_y$ 就是除了(1, y - 1), (1, 1), (y - 1,1)围成三角形以外的所有区域.这部分面积为 $1-(2-y)^2/2$ .因此

$F_Y(y)=\left\{\begin{matrix} 0 & ,y <0\\ \frac{y^2}{2} & , 0 \leq y < 1\\ 1- \frac{(2-y)^2}{2} & ,1 \leq y < 2\\ 1 & ,y \geq 2 \end{matrix}\right.$

对其求导,得PDF

$f_Y(y)=\left\{\begin{matrix} y &,0 \leq y \leq 1 \\ 2-y & ,1 \leq y \leq 2\\ 0 & ,otherwise \end{matrix}\right.$

本章完

未翻译:附录,课后作业