递归的简介
递归是一种十分重要的程序设计方法,对 于一些问题,用递归方法设计算法可使算 法简洁明了,逻辑清晰,易于设计
递归算法:直接或间接地调用自身的算法 。
递归函数:用函数自身给出定义的函数称 为递归函数。
递归关系:对原问题的求解可转化为对其 性质相同 的子问题的求解。
递归方法:用于解决一类满足递归关系的 问题
递归的例子

设计要素:边界条件,递归方程

递归算法设计要素
递归关系(特性):产生递归的基础
当算法中某步骤要通过解质相同的子问题实现时,该步骤用递归调用实现。
递归出口(结束条件):确定递归的层数
当子问题的规模充分小时可直接求解时,递归结束
参数设置
参数表示了原问题及其不同的子问题。参数表示了子问题的大小和状态,以区别原问题以及不同层次的子问题。
算法功能的设定
严格规定递归算法要解决什么样的问题。 算法功能的正确设定是保证递归过程正确进行的前提。
算法设计应注意
初始化,递归与循环,算法正确性的验证,…
递归程序模板
返回类型 Func(参数列表)
if (出口条件/可直接求解条件)
求解;
return 结果;
else
求解,利用到更小规模的子问题求解
return 结果;
整数幂问题
整数幂问题
– 问题描述:求实数x的n次幂(n为非负整数)。
– 蛮力解法:直接进行n-1次乘法

递归算法描述

详解

寻找多数问题
寻找多数
问题描述:求n个元素序列中的多数元素 ,多数元素为在序列中出现的次数多于n/2的元 素。
启发规则
一个序列不一定存在多数元素。
一个序列的多数元素若存在则唯一
递归关系:
通过对除去多对不同元素后的子序列 的多数元素问题的求解,可得到原序列的多数元 素问题的候选解。
注意:
子序列的多数元素只是原序列的候选多数 元素,必须验证。但若子序列不存在多数元素, 则原序列就一定不存在多数素。
算法的基本思想:
逐个扫描序列元素,不断除去 不同的元素对,得到新的子序列,对子序列做同 样的运算,直至序列扫描完毕。
递归出口:
序列已扫描完。
参数:
待扫描的子序列的起始位置,当前状态。
递归代码
Candidate(m,a):
j=m; c=a[m];count=1//这一步是首先将数组的未扫描初始值赋值给c,将下标赋值给j,count为计数器
while j<n and count>0//循环条件j作为数组下标不能超过数组长度,计数器要保证始终大于0,否则说明此元素不是候选解
j=j+1;//循环增大数组下标
if(a[j]==c)//判断之后的数组值是否跟之前选定的c值相等
count++;//相等计数器+1
else
count--;//不等计数器-1
end while//结束一次循环
if j=n;//表示数组已经全部遍历完成,递归终点,
else return candidate(j+1,a)//表示数组在j时,count就为0了,但是数组还没遍历完,要重新确定开始点,再次递归
//需要将子序列的多数元素与父序列进行验证
FindMajority(n,a):
c=Candidate(1,a);
count=0;
for j=1 to n
if a[j]= c then count=count+1;
if count> n/2+1
return c;
else
return none;
多项式求值
多项式求值
输入:x 浮点数;n 最高项幂; A[] 数组,包含n+1 各元素值
– 求多项式 P(x,A)=A[n]xn+...+A[i]xi+…+A[0]*x0 的值
要求采用两种算法实现,并编写完整的代码提交。
• 1 用逐个求每一项,在对各项累加的方法。(迭代求和,
在迭代的同时,可以把上一步的x^(n-1)加以利用,求x^n)
• 2 用Horner规则求多项式。
方法1
double P(x,n,A)
{
double t=1;P=0;//设置初始值
for(i=0...n)
{
P+=A[i++]*t//每次将P的值跟之前的P相加,新加的值为A[i]x^i,加完之后,每次将i+1
t*=x;//改变t使每次的t值与A[i]相匹配
}
return P;
}
方法2
调用HornerP(x,n,m,A)
HornerP(x,n,m,A) { if(m==0) return A[n]; else { p=x*HornerP(x,n,m-1,A)+A[n-m] return P; } }HORNER P=a{n} for j=1 to n p=xp+a{n-j} end for return P
解释
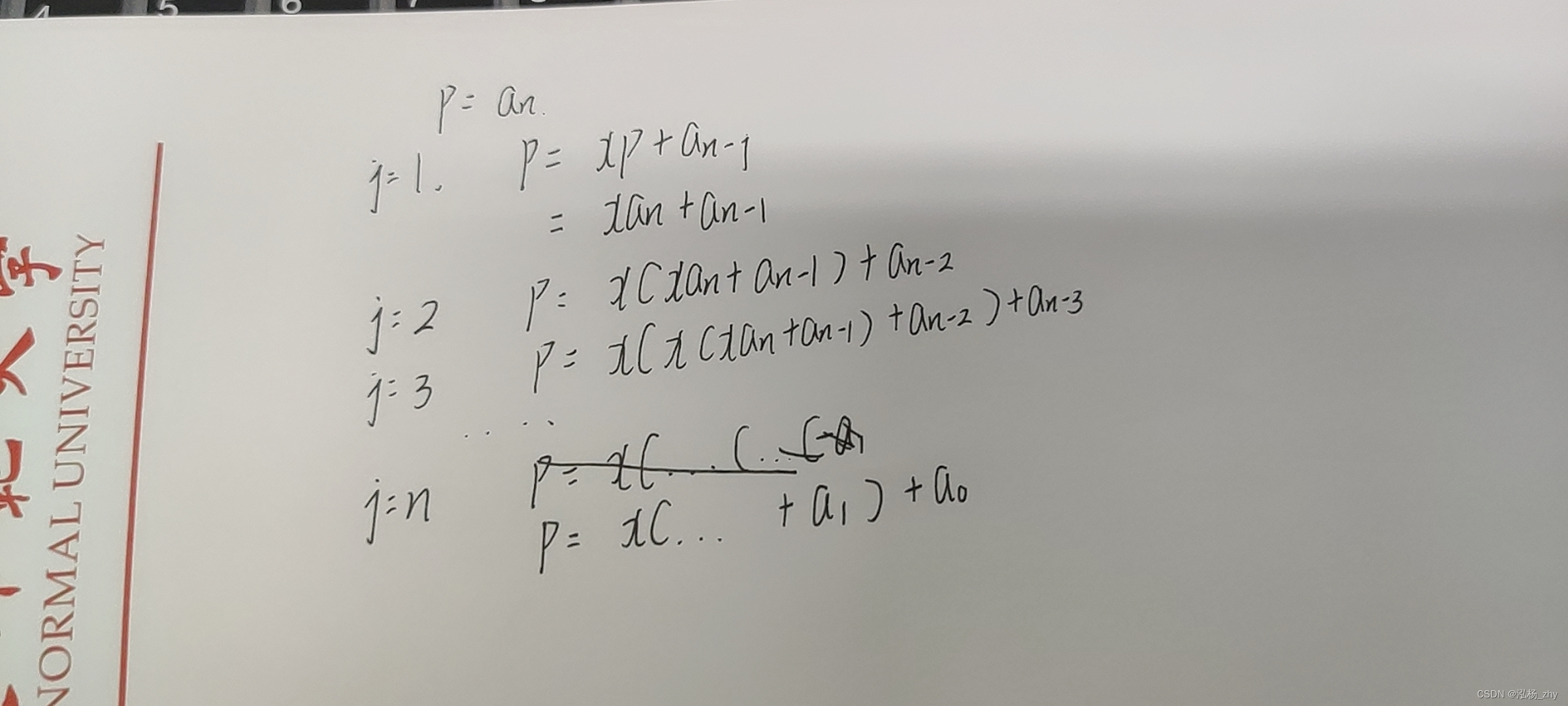








 本文深入探讨了递归算法的概念,包括递归函数、递归关系和递归方法。详细介绍了如何设计递归算法,强调了边界条件和递归方程的重要性。文中通过整数幂问题、寻找多数元素问题和多项式求值等实例展示了递归算法的实际应用,并提供了相应的递归代码实现。递归算法在解决复杂问题时能简化逻辑,但需注意避免无限循环和效率问题。
本文深入探讨了递归算法的概念,包括递归函数、递归关系和递归方法。详细介绍了如何设计递归算法,强调了边界条件和递归方程的重要性。文中通过整数幂问题、寻找多数元素问题和多项式求值等实例展示了递归算法的实际应用,并提供了相应的递归代码实现。递归算法在解决复杂问题时能简化逻辑,但需注意避免无限循环和效率问题。
















 2467
2467

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








