正整数中1出现的次数

题目描述

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数。

解题思路

考虑将n的十进制的每一位单独拿出讨论，每一位的值记为weight。

1) 个位

从1到n，每增加1，weight就会加1，当weight加到9时，再加1又会回到0重新开始。那么weight从0-9的这种周期会出现多少次呢？这取决于n的高位是多少，看图：

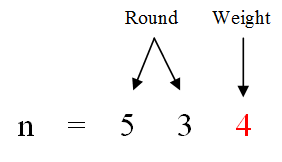
以534为例，在从1增长到n的过程中，534的个位从0-9变化了53次，记为round。每一轮变化中，1在个位出现一次，所以一共出现了53次。
再来看weight的值。weight为4，大于0，说明第54轮变化是从0-4，1又出现了1次。我们记1出现的次数为count，所以：
count = round+1 = 53 + 1 = 54
如果此时weight为0（n=530），说明第54轮到0就停止了，那么：
count = round = 53

2) 十位

对于10位来说，其0-9周期的出现次数与个位的统计方式是相同的，见图：

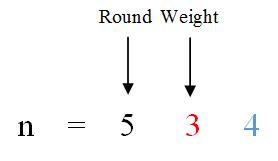
不同点在于：从1到n，每增加10，十位的weight才会增加1，所以，一轮0-9周期内，1会出现10次。即rount*10。
再来看weight的值。当此时weight为3，大于1，说明第6轮出现了10次1，则：
count = round*10+10 = 5*10+10 = 60
如果此时weight的值等于0（n=504），说明第6轮到0就停止了，所以：
count = round*10+10 = 5*10 = 50
如果此时weight的值等于1（n=514），那么第6轮中1出现了多少次呢？很明显，这与个位数的值有关，个位数为k，第6轮中1就出现了k+1次(0-k)。我们记个位数为former，则：
count = round*10+former +1= 5*10+4 = 55

3) 更高位

更高位的计算方式其实与十位是一致的，不再阐述。

4) 总结

将n的各个位分为两类：个位与其它位。
对个位来说：

• 若个位大于0，1出现的次数为round*1+1
• 若个位等于0，1出现的次数为round*1

对其它位来说，记每一位的权值为base，位值为weight，该位之前的数是former，举例如图：

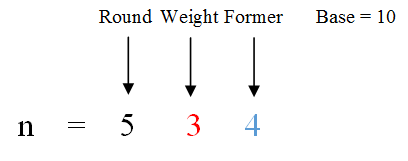
则：

• 若weight为0，则1出现次数为round*base
• 若weight为1，则1出现次数为round*base+former+1
• 若weight大于1，则1出现次数为rount*base+base

比如：

• 534 = （个位1出现次数）+（十位1出现次数）+（百位1出现次数）=（53*1+1）+（5*10+10）+（0*100+100）= 214
• 530 = （53*1）+（5*10+10）+（0*100+100） = 213
• 504 = （50*1+1）+（5*10）+（0*100+100） = 201
• 514 = （51*1+1）+（5*10+4+1）+（0*100+100） = 207
• 10 = (1*1)+(0*10+0+1) = 2

5. 完整代码

package JianZhiOffer;

public class NumberOf1Between1AndN_Solution
{

    public static void main(String[] args)
    {
        int n=534;
        int a=NumberOf1Between1AndN_Solution(n);
        System.out.println(a);

    }
    public static int NumberOf1Between1AndN_Solution(int n)
    {
      if(n<1)
            return 0;
      int count=0;
      int base=1;
      int round=n;
      while(round>0)
      {  
         int weight= round%10;
         round/=10;
         count+=round*base;
         if(weight==1)
             count+=n%base+1;
         if(weight>1)
             count+=base;
         base*=10;
      }
        return count;
        }
}
/*
 * 假设count为534，第一次进入while循环后为53，第二次为5，第三次为0，然后便退出。分别对应个位，十位，百位，
 * 如果位数多，依次类推即可
 */
实验结果：214

即： （53+1）+（50+10）+（0+100）=214

  
  
2
3
46. 时间复杂度分析

时间复杂度：

由分析思路或者代码都可以看出，while循环的次数就是n的位数,logn（以10为底），而循环体内执行的操作都是有限次的，所以时间复杂度为O(logn)。