一 单位向量
如果向量 α的模为1, 即|α| =1, 则称α为单位向量。
如果α≠ 0, 记 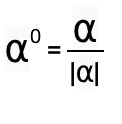 , α ⁰称之为 α的单位化向量,它的长度为1, 并且有 α = |α| α ⁰
, α ⁰称之为 α的单位化向量,它的长度为1, 并且有 α = |α| α ⁰
二 向量与坐标轴的夹角
单位向量的三个坐标是向量的方向角余弦。
先看一个定理性质的例题

接着看一个应用的例题

再看一个题目
设向量的方向余弦分别满足: (1) cosa = 0; (2) cosβ = 1; (3) cosa = 0, cosβ = 0. 问这些向量与坐标轴的关系如何?
解:

如果向量 α的模为1, 即|α| =1, 则称α为单位向量。
如果α≠ 0, 记 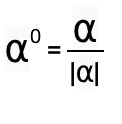 , α ⁰称之为 α的单位化向量,它的长度为1, 并且有 α = |α| α ⁰
, α ⁰称之为 α的单位化向量,它的长度为1, 并且有 α = |α| α ⁰
单位向量的三个坐标是向量的方向角余弦。
先看一个定理性质的例题

接着看一个应用的例题

再看一个题目
设向量的方向余弦分别满足: (1) cosa = 0; (2) cosβ = 1; (3) cosa = 0, cosβ = 0. 问这些向量与坐标轴的关系如何?
解:


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


