数学基础补充归纳大纲（持续更新...）

1. 先验概率、后验概率、贝叶斯的区别和联系？

这篇讲得比较好 https://blog.csdn.net/yewei11/article/details/50537648

2. 协方差和相关性有什么区别？

相关性是协方差的标准化格式。协方差本身很难做比较。例如：如果我们计算工资（$）和年龄（岁）的协方差，因为这两个变量有不同的度量，所以我们会得到不能做比较的不同的协方差。

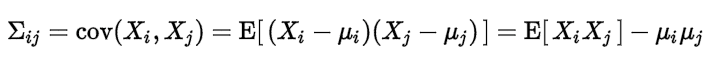
为了解决这个问题，我们计算相关性来得到一个介于-1和1之间的值，就可以忽略它们各自不同的度量。

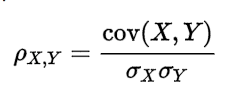
3.似然函数、最大似然估计、最小二乘、梯度下降

• 似然函数
  我们假设f是一个概率密度函数，那么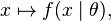是一个条件概率密度函数（θ 是固定的）
  而反过来，叫做似然函数 （x是固定的）。一般把似然函数写成
  θ是因变量。
• 最大似然估计
  而最大似然估计 就是求在θ的定义域中，当似然函数取得最大值时θ的大小。
  最大似然估计，就是利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。
• 最小二乘法
  最小二乘法我理解的是未知事件，求如何使得该事件最可能发生
• 最小二乘和极大似然是构造目标函数的方法，梯度下降是优化算法。
  优化方法中，有一类是使用函数的梯度信息，包括一阶的方法，例如梯度下降，以及二阶的方法，例如牛顿法等。当然，还有和梯度无关的方法，例如 fixed point iteration，坐标下降等等。
  机器学习的核心是一个model，一个loss fuction，再加上一个优化的算法。一个目标函数可以用不同的优化算法，不同的目标函数也可以用相同的优化算法。所以最小二乘和极大似然根本不是算法，和梯度下降毫无可比性。
  最小二乘和极大似然也不是对立的。
  最小二乘是从函数形式上来看的，极大似然是从概率意义上来看的。事实上，最小二乘可以由高斯噪声假设+极大似然估计推导出来。当然极大似然估计还可以推导出其他的loss function,比如logistic回归中，loss function是交叉熵.
  最小二乘法和梯度下降法的异同：
  http://blog.csdn.net/u010922227/article/details/77748493

参考：王芊 https://www.zhihu.com/question/24900876/answer/29375743

4.拉格朗日乘数法

拉格朗日乘子法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。
基本形态：
上述讨论的问题均为等式约束优化问题，但等式约束并不足以描述人们面临的问题——>不等式约束优化问题
KKT条件
参考：http://blog.csdn.net/pipisorry/article/details/52135854

5. 统计判决

• 最小误判概率准则判决
• 最小损失准则判决
• 最小最大损失准则
• N-P（Neyman-Pearson）判决