二叉树详细介绍与代码生成遍历

树的概念及其结构

要了解二叉树，那么首要的就是要知道树的概念。

在计算机科学中，树是一种广泛使用的抽象数据类型，用于模拟层次结构，树由节点构成。在这种层级系统中，存在一个最顶层的节点，称为根节点，它没有父节点。树中的其他节点可以有一个（在非二叉树中）或多个子节点，但只有一个父节点，除了根节点外。

树结构的基本术语：

• 节点（Node）: 树的基本部分，可能包含一个值或数据，并可能有子节点。
• 根节点（Root）: 树的顶端节点，没有父节点。
• 叶子节点（Leaf nodes）: 没有子节点的节点。
• 子节点（Child nodes）: 某个节点的直接后继节点。
• 父节点（Parent node）: 某个节点的直接前驱节点。
• 兄弟节点（Sibling nodes）: 具有相同父节点的节点。
• 边（Edge）: 连接节点的线，它定义了节点之间的父子关系。
• 路径（Path）: 从一个节点到另一个节点的边的序列。
• 深度（Depth）: 从根节点到某个节点的边的数目。
• 高度（Height）: 一个节点到最远叶子节点的最长路径的边的数目。树的高度是其所有节点高度的最大值。

下图是树的结构示意图

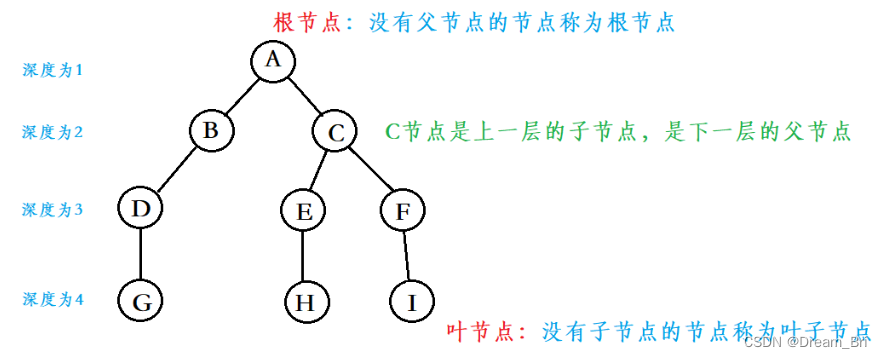
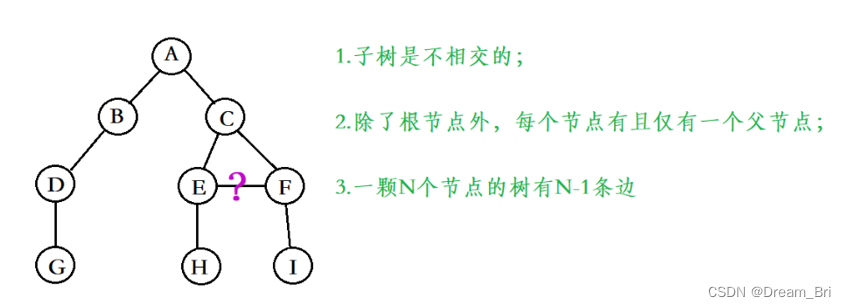
树结构没有循环或闭环，这是它和图结构的主要区别，如下就不能称作是树结构，因为子树之间有相交。

树的构造——代码表示

class TreeNode:
    def __init__(self, value):
        self.value = value  # 当前节点的值
        self.children = []  # 子节点的列表

    def add_child(self, child_node):
        """添加子节点"""
        self.children.append(child_node)

    def remove_child(self, child_node):
        """移除子节点"""
        self.children = [child for child in self.children if child is not child_node]

    def traverse(self):
        """遍历树节点"""
        nodes_to_visit = [self]
        while len(nodes_to_visit) > 0:
            current_node = nodes_to_visit.pop()
            print(current_node.value)
            nodes_to_visit.extend(current_node.children)

# 示例构造树
root = TreeNode('Root')
child1 = TreeNode('Child1')
child2 = TreeNode('Child2')
child3 = TreeNode('Child3')

root.add_child(child1)
root.add_child(child2)
child1.add_child(child3)

# 遍历和打印树
root.traverse()

上述代码定义了一个树节点，它包含一个值和一个子节点列表。并且可以添加或移除子节点，并有一个用于遍历树的方法，它采用深度优先遍历（Depth-First Search, DFS）的方式来访问每个节点。

这个例子中构建的树结构如下所示：

当运行 root.traverse() 方法时，它会打印出：

Root
Child1
Child3
Child2