算法时间复杂度分析

 简单而言，算法时间复杂度就是数学里面的函数，也就是算法的时间度量，一般记作：T(n)=O( f(n) )。

算法分析的分类：

  1.最坏情况：任意输入规模的最大运行时间。（上界）

  2.平均情况：任意输入规模的期望运行时间。

  3.最好情况：任意输入规模的最小运行时间，通常最好情况不会出现。（下界）

  情景一：(常数阶）

int sum=0,n=2;
sum+=n;
printf("sum=%d",sum);

算法的执行次数f(n)=3,一般用常数1取代加法常数，因此算法的时间复杂度为O(1).

  情景二：（线性阶）

void test1(int n)
{
	for(int i=0;i<n;i++)
	{
		//...
	}
}

算法的执行次数f(n)=n,因此算法的时间复杂度为O(n).

 情景三：(平方阶）

void test2(int n)
{
	int m=5;
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			//...
		}
	}
	for(int k=0;k<2 * n;k++)
	{
		//...
	}
	while(m--)
	{
		//...
	}
}

算法的执行次数为f(n)=n^2+2n+5,一般关注算法的最坏运行情况，关注n^2,算法的时间复杂度为O(n^2).

情景四：（指数阶）

引入：递归算法的时间复杂度：递归总次数*每次递归次数；

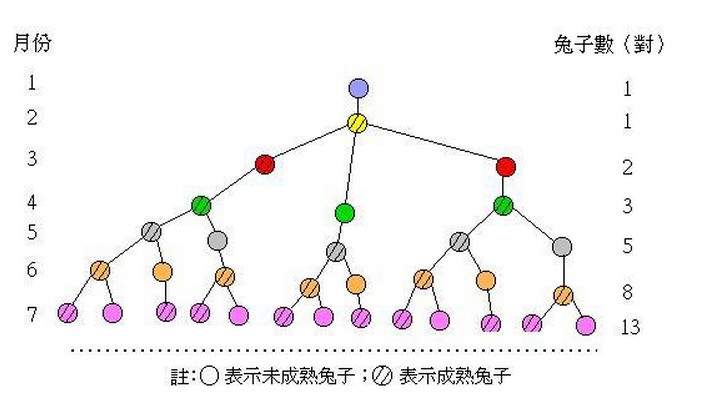
斐波那契数列：

• 第一个月初有一对刚诞生的兔子
• 第二个月后（第三个月初）它们可以生育
• 每月每对可生育的兔子会诞生下一对新兔子
• 兔子永不死去

#include <iostream>
using namespace std;

unsigned long long Fibonacci(size_t n)
{
	return n<2 ? n:Fibonacci(n-2)+Fibonacci(n-1);
}

int main()
{
	size_t n;
	cin>>n;
	unsigned long long m=0;
	m=Fibonacci(n);
	cout<<m<<endl;
	getchar();
	return 0;
}

当我们用递归法写斐波那契数列，对程序进行不断测试时会发现：输入45时，程序会运行好长时间，算法执行效率太低了。

仔细分析一下（类似于完全二叉树），算法的执行次数为f(n)=2^n-1，关注算法的最坏运行情况，算法的时间复杂度为O(2^n)。

此时，我们应该优化一下程序：

#include <iostream>
using namespace std;

unsigned long long* Fibonacci(size_t n)
{
	int i;
	unsigned long long* a=new unsigned long long[n+1];
        a[0]=0;
	a[1]=1;
	for(i=2;i<=n;i++)
	{
		a[i]=a[i-1]+a[i-2];
	}
	return a;
}

int main()
{
	size_t n;
	int i;
	cout<<"数列长度为:";
	cin>>n;
    unsigned long long *a;
	a=Fibonacci(n);
	cout<<"Fibonacci数列:"<<endl;
	for(i=1;i<=n;i++)
	{
		cout<<a[i]<<"->";
	}

	cout<<"over"<<endl;
	getchar();
	return 0;
}

情景五：(对数阶）

折半查找：(用图示代替代码）

观察图我们发现，我们需要查找所需要元素时，会将确定区域不断分成2份，知道找到元素为止，由2^x=N得算法的执行次数f(n)=log2N,时间复杂度为O(logn).

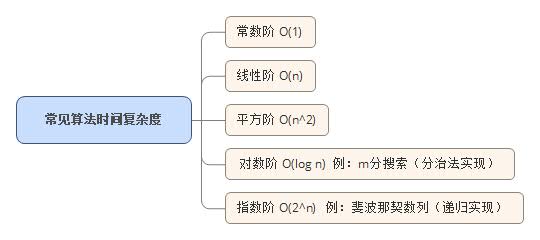
总结：