Physically Based Rendering——史上最容易理解的BRDF中D函数NDF的中文资料

本文链接：https://blog.csdn.net/xingzhe2001/article/details/83897914

本文深入探讨了基于物理的渲染（PBR）中BRDF的法线分布函数（NDF），包括Torrance Sparrow（高斯分布）、Phong模型、Beckmann分布和Trowbridge-Reitz（GGX）模型。通过公式、代码和渲染效果展示各模型特点，帮助读者更好地理解BRDF的D函数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

粗糙度决定了D函数的分布，一般粗糙度是D函数的方差

本文假定读者已经对PBR即Physcially Based Rendering 基于物理的渲染有了初步的了解，对于PBR的入门有很多文章都介绍的不错。

本文针对想再了解下BRDF双向反射分布函数里的推导与内容的读者，是我自己学习BRDF的笔记

这篇文章主要介绍BRDF里的法线分布函数D函数的各种算法于思想

D函数描述了微表面有多少比例的微表面的朝向是可以把光反射到眼睛的。

之前我的博客手推系列——直观理解推导Physically Based Rendering 的BRDF公式之微表面法线分布函数NDF

用暴力的方式展示了NDF的概念和大题样子

假设高度图是平均分布，那么计算的NDF样子

假设高度图是高斯分布，那么计算的NDF样子

下面介绍一些流行的NDF的公式和思想

Torrance Sparrow D函数或者高斯分布

来自与论文 Theory for Off-Specular Reflection From Roughened Surfaces Author

考虑一个斜率分布是高斯分布的微表面，很明显朝向某个方向的微表面的比例也满足高斯分布。这就是著名的高斯分布D函数，就是Torrance and Sparrow的BRDF模型里用的D函数，原始论文是这么写的

$P=P(\alpha)=b\ exp(-c^2\alpha^2)$

Blinn说的Torrance and Sparrow D函数是这样的

$D_2=e^{-(\alpha c_2)^2}$

看起来这个样子

#Blinn说的Torrance and Sparrow 高斯分布D函数  from cook paper
def TorranceSparrow_D(roughness, theta):
    c = 1
    return c * np.exp(-np.power(theta/roughness,2))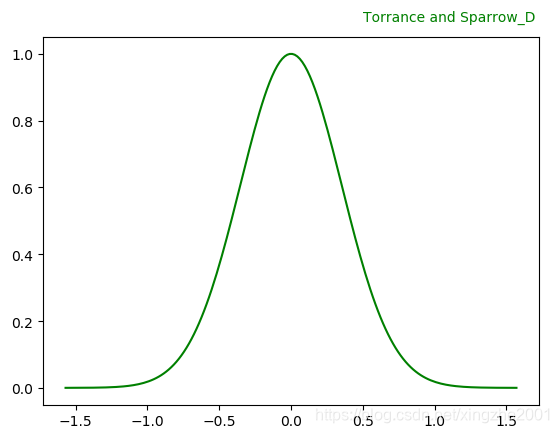

其中b,c 是常数，b是微表面法线方向为宏观表面时候法线方向的时候的概率，c明显是正态分布的标准差的导数。

a是微表面法线和宏观法线的夹角。现在一般流行叫做 NoH

Physically Based Rendering——史上最容易理解的BRDF中D函数NDF的中文资料

Torrance Sparrow D函数 或者 高斯分布

Torrance Sparrow D函数或者高斯分布