[leetcode] 62. Unique Paths

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

思路：
第一种方法：

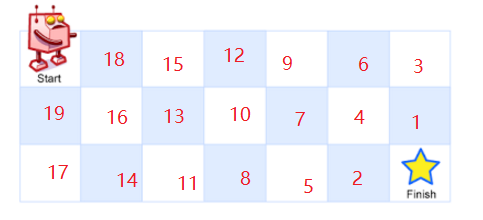
到达finish的方法数，是到达1和达到2方法的和，而到达1的方法是到达4和到达3方法的总和，到达2是到达4和到达5方法的综合依次类推，
因为只能向右或向下故第一行和第一列位置到达的方法数为1，
用一个m*n的二位数组存储到达各个方框的次数二维数组[m-1][n-1]保存的数即为最终结果。时间复杂度O(m*n)，空间复杂度O(m*n);

第二种方法：
以题目给出的3*7为例，到达finish需要向下移动2次，向右移动6次 总共8次，这就转化成组合问题，从8步中选择两步向下移动其余向右移动，即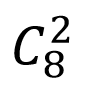 空间复杂度为O(1);

方法一：
具体代码如下:

public class Solution {
    public int uniquePaths(int m, int n) {
        int result = 0;
        if(m ==0 || m ==0){
            return 0;
        }

        int[][] nums = new int[m][n];

        for(int i = 0; i < n; i++){
            nums[0][i] = 1;
        }
        for(int i = 0; i < m; i++){
            nums[i][0] = 1;
        }

        for(int i = 1; i < m;i++){
            for(int j = 1; j < n; j++){
                nums[i][j] = nums[i][j-1]+ nums[i-1][j];
            }
        }

        result = nums[m-1][n-1];
        return result;
    }
}

方法二：
具体代码如下:

public class Solution {
    public int uniquePaths(int m, int n) {
        long result = 1;
        if (m == 1 || n == 1) {
            return (int)result;
        }

        int x = m > n ? m : n;
        int y = m < n ? m : n;
        int chu = 1;

        int zonghe = m+n-2;
        for(int i =0; i < y-1; i++){
            result = result * (zonghe-i);

        }
        for(int i =0; i < y-1; i++){
            chu = chu * (i+1);
        }
        return (int)(result/chu);
    }
}