代码随想录算法训练营第五十七天 | prim算法精讲、kruskal算法精讲

最新推荐文章于 2024-10-01 23:05:47 发布

夕一之欧

最新推荐文章于 2024-10-01 23:05:47 发布

阅读量1k

点赞数 7

分类专栏：代码随想录算法训练营文章标签：算法

本文链接：https://blog.csdn.net/xizhou_sean/article/details/141727849

版权

代码随想录算法训练营专栏收录该内容

53 篇文章 0 订阅

订阅专栏

prim算法精讲

1、题目

题目描述：

在世界的某个区域，有一些分散的神秘岛屿，每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路，方便运输。

不同岛屿之间，路途距离不同，国王希望你可以规划建公路的方案，如何可以以最短的总公路距离将所有岛屿联通起来。

给定一张地图，其中包括了所有的岛屿，以及它们之间的距离。以最小化公路建设长度，确保可以链接到所有岛屿。

输入描述：

第一行包含两个整数V 和 E，V代表顶点数，E代表边数。顶点编号是从1到V。例如：V=2，一个有两个顶点，分别是1和2。

接下来共有 E 行，每行三个整数 v1，v2 和 val，v1 和 v2 为边的起点和终点，val代表边的权值。

输出描述：

输出联通所有岛屿的最小路径总距离

输入示例：

输出示例：

2、题解

本题是最小生成树的模板题，那么我们来讲一讲最小生成树。

最小生成树可以使用 prim算法也可以使用 kruskal算法计算出来。

本篇我们先讲解 prim算法。

最小生成树是所有节点的最小连通子图，即：以最小的成本（边的权值）将图中所有节点链接到一起。

图中有n个节点，那么一定可以用 n - 1 条边将所有节点连接到一起。

那么如何选择这 n-1 条边就是最小生成树算法的任务所在。

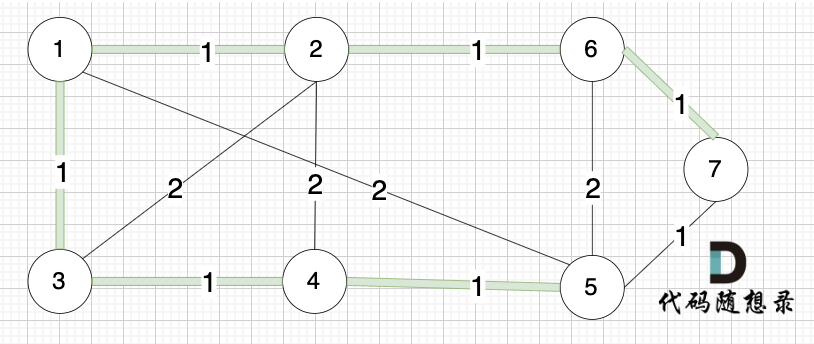
例如本题示例中的无向有权图为：

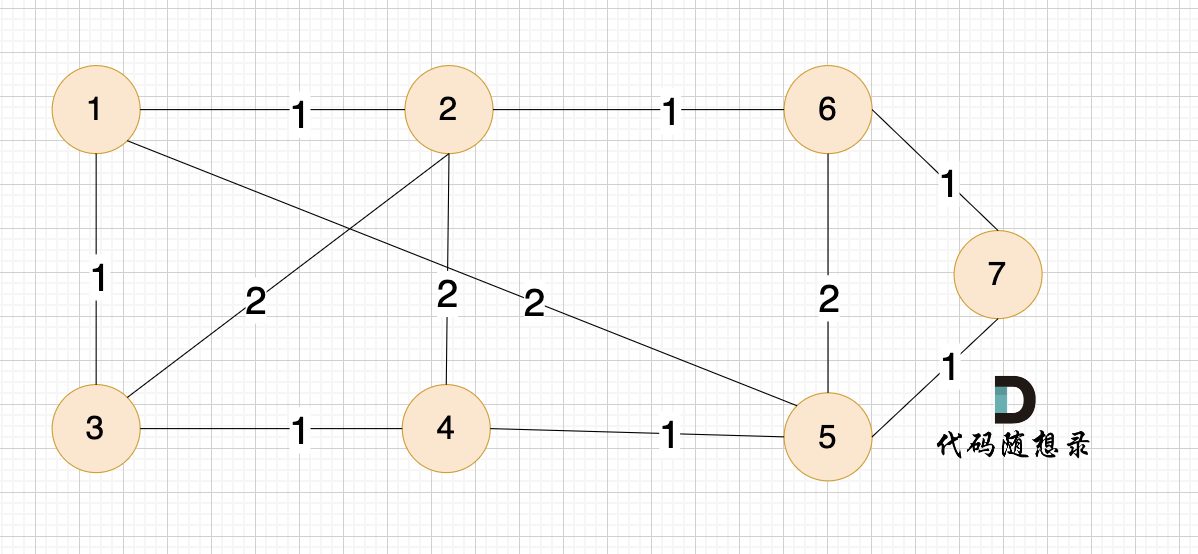
那么在这个图中，如何选取 n-1 条边使得图中所有节点连接到一起，并且边的权值和最小呢？

（图中为n为7，即7个节点，那么只需要 n-1 即 6条边就可以讲所有顶点连接到一起）

prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。

prim算法核心就是三步，我称为prim三部曲，大家一定要熟悉这三步，代码相对会好些很多：

第一步，选距离生成树最近节点
第二步，最近节点加入生成树
第三步，更新非生成树节点到生成树的距离（即更新minDist数组）

现在录友们会对这三步很陌生，不知道这是干啥的，没关系，下面将会画图举例来带大家把这prim三部曲理解到位。

在prim算法中，有一个数组特别重要，这里我起名为：minDist。

刚刚我有讲过 “每次寻找距离最小生成树最近的节点并加入到最小生成树中”，那么如何寻找距离最小生成树最近的节点呢？

这就用到了 minDist 数组，它用来作什么呢？

minDist数组用来记录每一个节点距离最小生成树的最近距离。理解这一点非常重要，这也是 prim算法最核心要点所在，很多录友看不懂prim算法的代码，都是因为没有理解透这个数组的含义。

接下来，我们来通过一步一步画图，来带大家巩固 prim三部曲 以及 minDist数组的作用。

（示例中节点编号是从1开始，所以为了让大家看的不晕，minDist数组下标我也从 1 开始计数，下标0 就不使用了，这样下标和节点标号就可以对应上了，避免大家搞混）

1 初始状态

minDist 数组里的数值初始化为最大数，因为本题节点距离不会超过 10000，所以初始化最大数为 10001就可以。

相信这里录友就要问了，为什么这么做？

现在还没有最小生成树，默认每个节点距离最小生成树是最大的，这样后面我们在比较的时候，发现更近的距离，才能更新到 minDist 数组上。

如图：

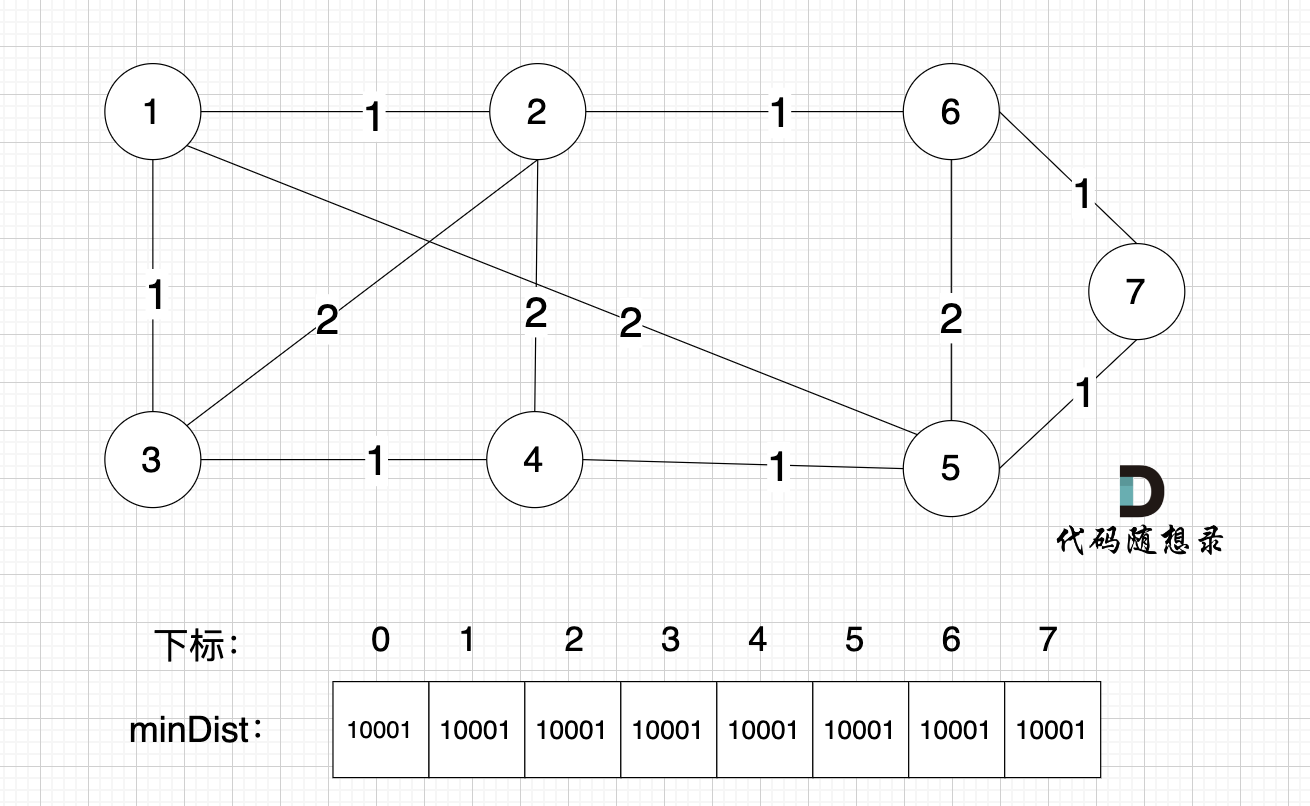
开始构造最小生成树

2

1、prim三部曲，第一步：选距离生成树最近节点

选择距离最小生成树最近的节点，加入到最小生成树，刚开始还没有最小生成树，所以随便选一个节点加入就好（因为每一个节点一定会在最小生成树里，所以随便选一个就好），那我们选择节点1 （符合遍历数组的习惯，第一个遍历的也是节点1）

2、prim三部曲，第二步：最近节点加入生成树

此时节点1 已经算最小生成树的节点。

3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）

接下来，我们要更新所有节点距离最小生成树的距离，如图：

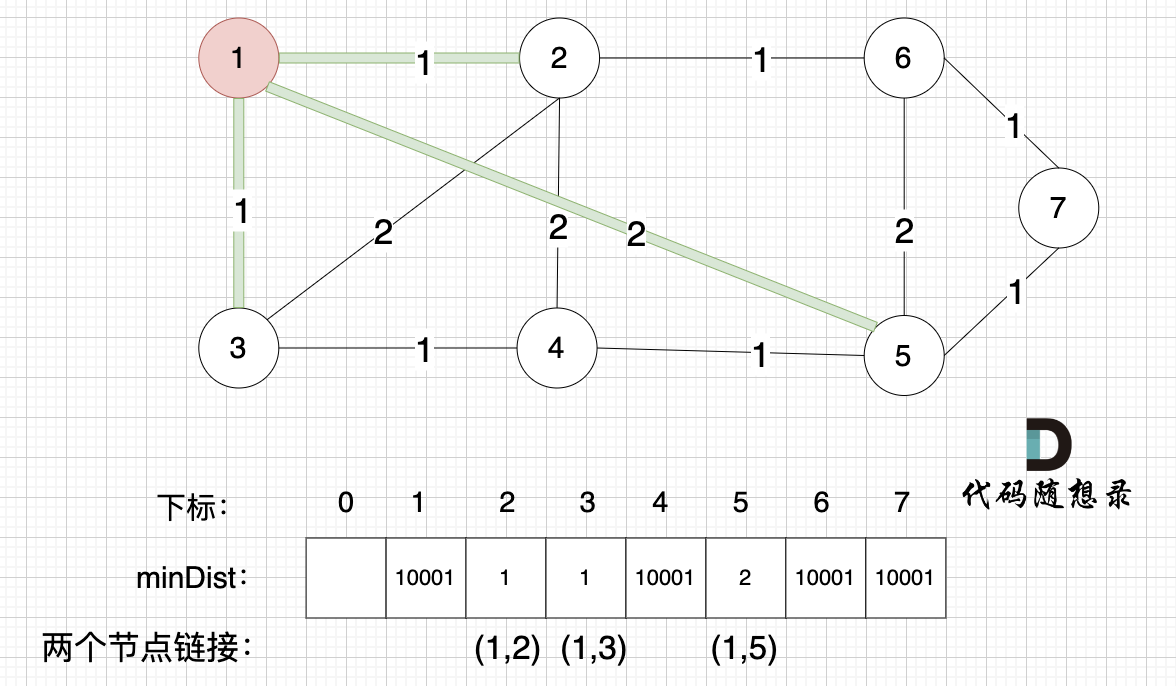
注意下标0，我们就不管它了，下标 1 与节点 1 对应，这样可以避免大家把节点搞混。

此时所有非生成树的节点距离最小生成树（节点1）的距离都已经跟新了。

节点2 与节点1 的距离为1，比原先的距离值10001小，所以更新minDist[2]。
节点3 和节点1 的距离为1，比原先的距离值10001小，所以更新minDist[3]。
节点5 和节点1 的距离为2，比原先的距离值10001小，所以更新minDist[5]。

注意图中我标记了 minDist数组里更新的权值，是哪两个节点之间的权值，例如 minDist[2] =1 ，这个 1 是节点1 与节点2 之间的连线，清楚这一点对最后我们记录最小生成树的权值总和很重要。

（我在后面依然会不断重复 prim三部曲，可能基础好的录友会感觉有点啰嗦，但也是让大家感觉这三部曲求解的过程）

3

1、prim三部曲，第一步：选距离生成树最近节点

选取一个距离最小生成树（节点1）最近的非生成树里的节点，节点2，3，5 距离最小生成树（节点1）最近，选节点 2（其实选节点3或者节点2都可以，距离一样的）加入最小生成树。

2、prim三部曲，第二步：最近节点加入生成树

此时节点1 和节点2，已经算最小生成树的节点。

3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）

接下来，我们要更新节点距离最小生成树的距离，如图：

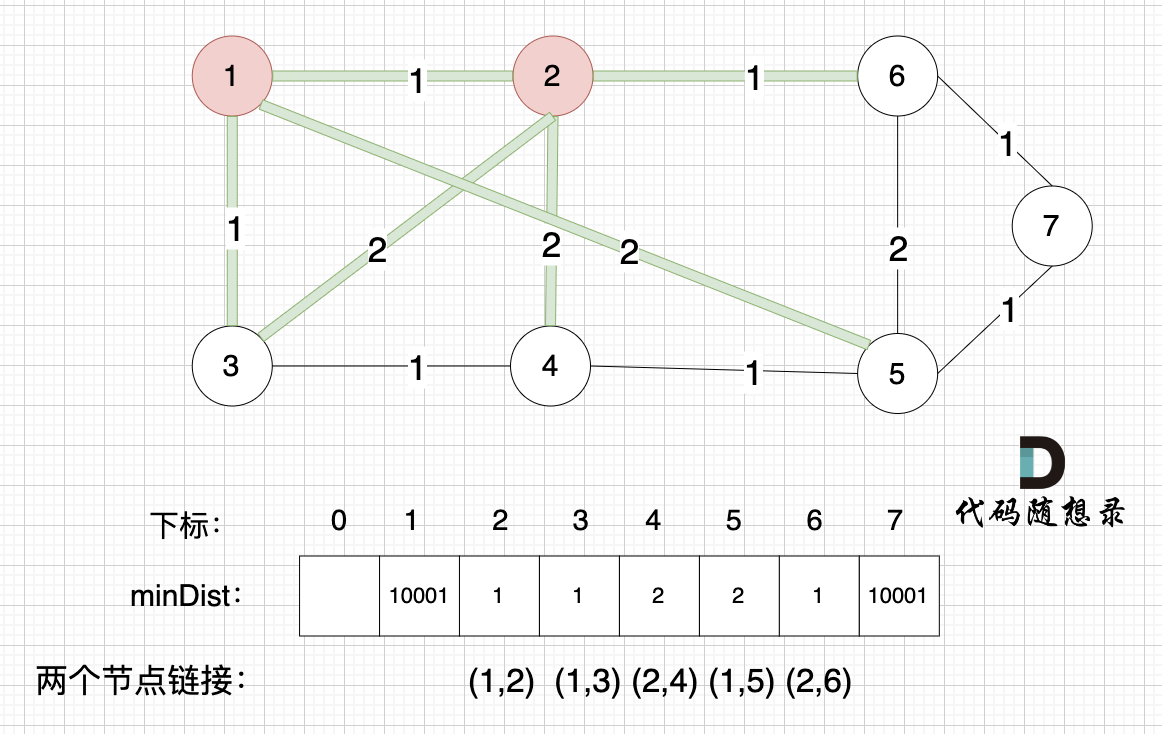
此时所有非生成树的节点距离最小生成树（节点1、节点2）的距离都已经跟新了。

节点3 和节点2 的距离为2，和原先的距离值1 小，所以不用更新。
节点4 和节点2 的距离为2，比原先的距离值10001小，所以更新minDist[4]。
节点5 和节点2 的距离为10001（不连接），所以不用更新。
节点6 和节点2 的距离为1，比原先的距离值10001小，所以更新minDist[6]。

4

1、prim三部曲，第一步：选距离生成树最近节点

选择一个距离最小生成树（节点1、节点2）最近的非生成树里的节点，节点3，6 距离最小生成树（节点1、节点2）最近，选节点3 （选节点6也可以，距离一样）加入最小生成树。

2、prim三部曲，第二步：最近节点加入生成树

此时节点1 、节点2 、节点3 算是最小生成树的节点。

3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）

接下来更新节点距离最小生成树的距离，如图：

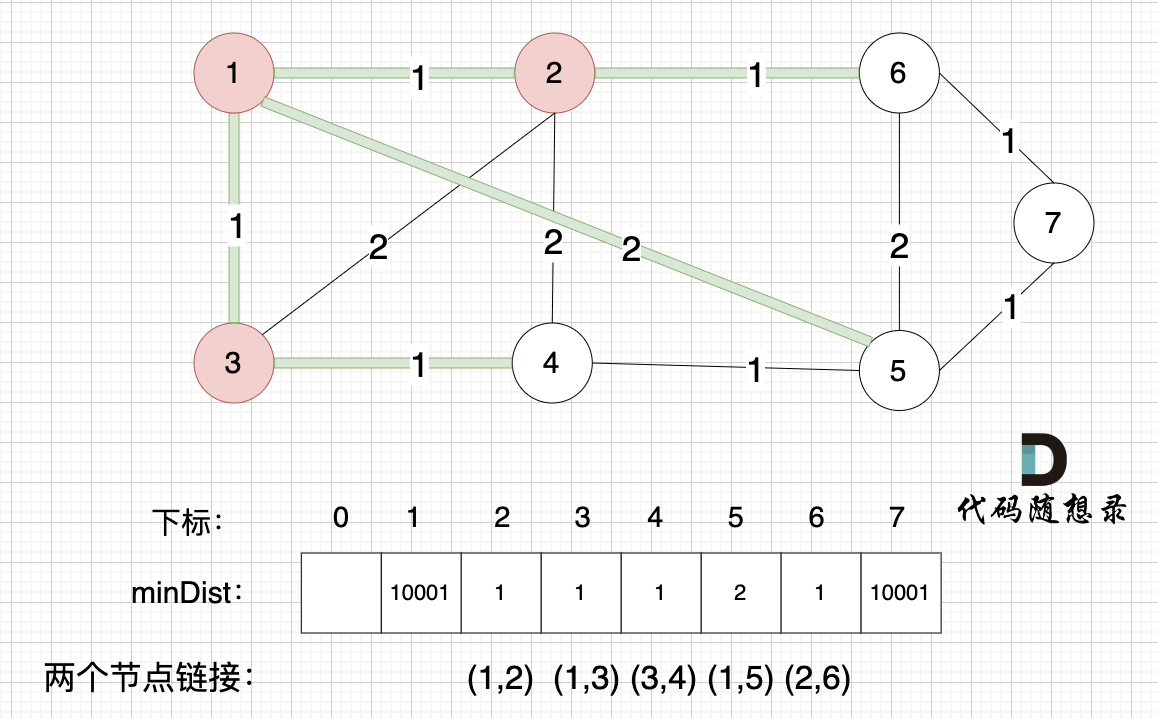
所有非生成树的节点距离最小生成树（节点1、节点2、节点3 ）的距离都已经跟新了。

节点 4 和节点 3的距离为 1，和原先的距离值 2 小，所以更新minDist[3]为1。

上面为什么我们只比较节点4 和节点3 的距离呢？

因为节点3加入最小生成树后，非生成树节点只有节点 4 和节点3是链接的，所以需要重新更新一下节点4距离最小生成树的距离，其他节点距离最小生成树的距离都不变。

5

1、prim三部曲，第一步：选距离生成树最近节点

继续选择一个距离最小生成树（节点1、节点2、节点3）最近的非生成树里的节点，为了巩固大家对 minDist数组的理解，这里我再啰嗦一遍：

minDist数组是记录了所有非生成树节点距离生成树的最小距离，所以从数组里我们能看出来，非生成树节点 4 和节点 6 距离生成树最近。

任选一个加入生成树，我们选节点4（选节点6也行）。

注意，我们根据 minDist数组，选取距离生成树最近的节点加入生成树，那么 minDist数组里记录的其实也是最小生成树的边的权值（我在图中把权值对应的是哪两个节点也标记出来了）。

如果大家不理解，可以跟着我们下面的讲解，看 minDist数组的变化， minDist数组里记录的权值对应的哪条边。

理解这一点很重要，因为最后我们要求最小生成树里所有边的权值和。

2、prim三部曲，第二步：最近节点加入生成树

此时节点1、节点2、节点3、节点4 算是最小生成树的节点。

3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）

接下来更新节点距离最小生成树的距离，如图：

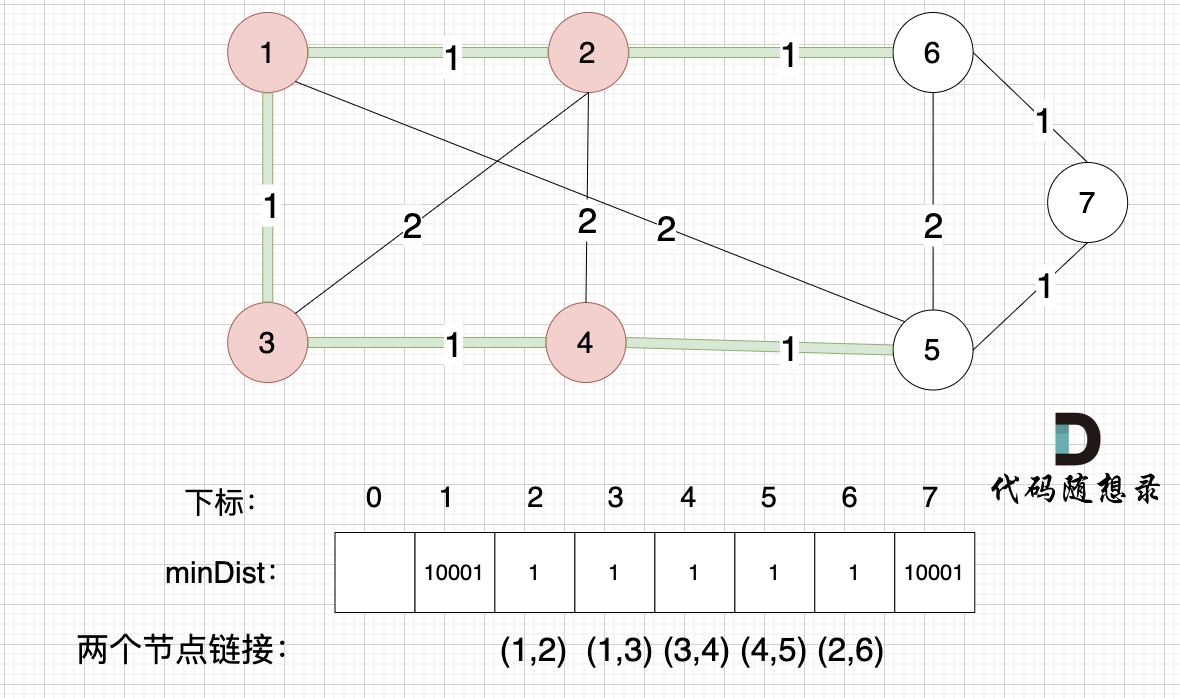
minDist数组已经更新了所有非生成树的节点距离最小生成树（节点1、节点2、节点3、节点4 ）的距离。

节点 5 和节点 4的距离为 1，和原先的距离值 2 小，所以更新minDist[4]为1。

6

1、prim三部曲，第一步：选距离生成树最近节点

继续选距离最小生成树（节点1、节点2、节点3、节点4 ）最近的非生成树里的节点，只有节点 5 和节点6。

选节点5 （选节点6也可以）加入生成树。

2、prim三部曲，第二步：最近节点加入生成树

节点1、节点2、节点3、节点4、节点5 算是最小生成树的节点。

3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）

接下来更新节点距离最小生成树的距离，如图：

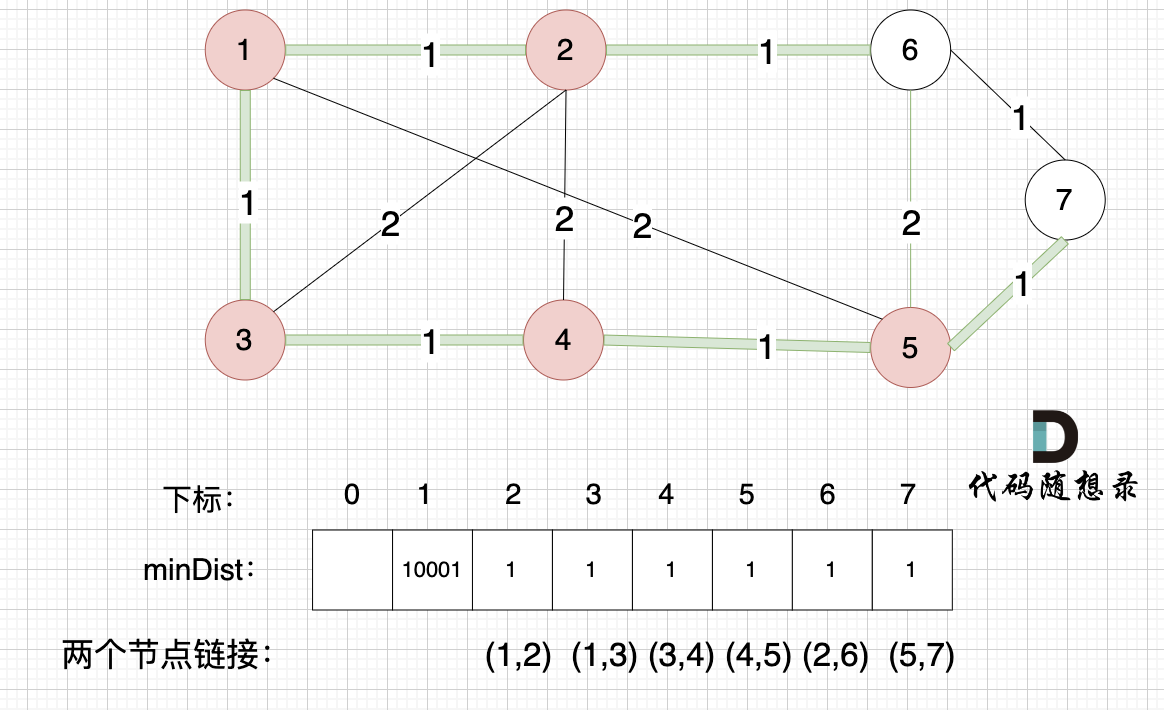
minDist数组已经更新了所有非生成树的节点距离最小生成树（节点1、节点2、节点3、节点4 、节点5）的距离。

节点 6 和节点 5 距离为 2，比原先的距离值 1 大，所以不更新
节点 7 和节点 5 距离为 1，比原先的距离值 10001小，更新 minDist[7]

7

1、prim三部曲，第一步：选距离生成树最近节点

继续选距离最小生成树（节点1、节点2、节点3、节点4 、节点5）最近的非生成树里的节点，只有节点 6 和节点7。

2、prim三部曲，第二步：最近节点加入生成树

选节点6 （选节点7也行，距离一样的）加入生成树。

3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）

节点1、节点2、节点3、节点4、节点5、节点6 算是最小生成树的节点，接下来更新节点距离最小生成树的距离，如图：

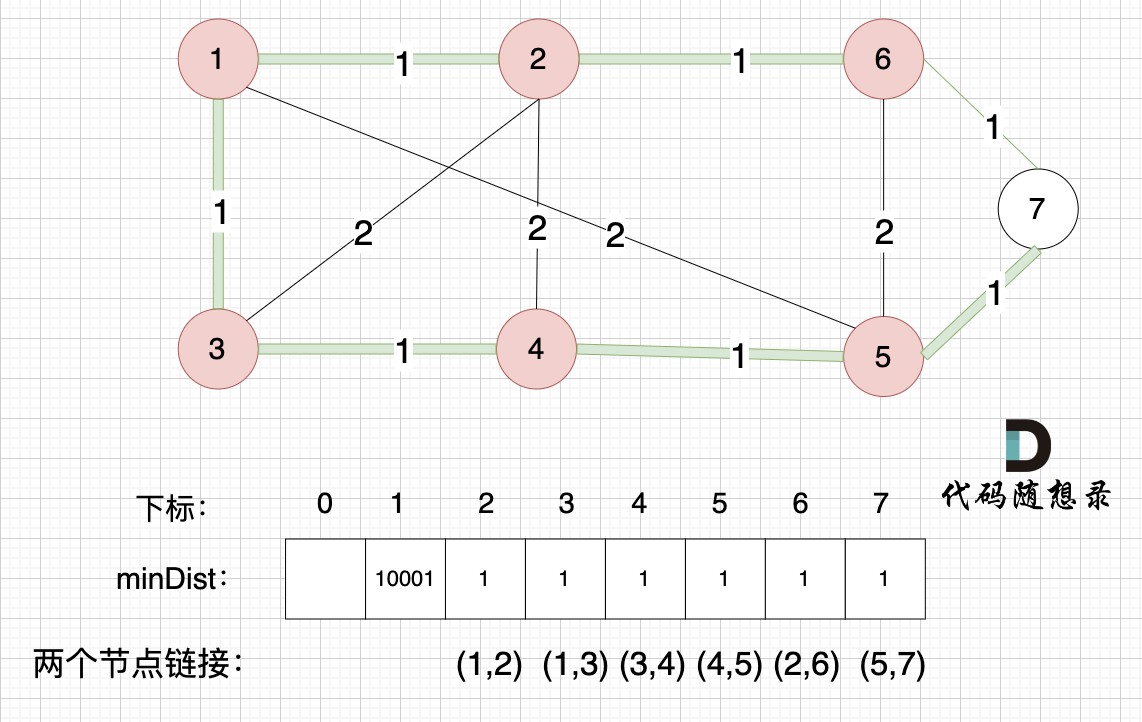
这里就不在重复描述了，大家类推，最后，节点7加入生成树，如图：

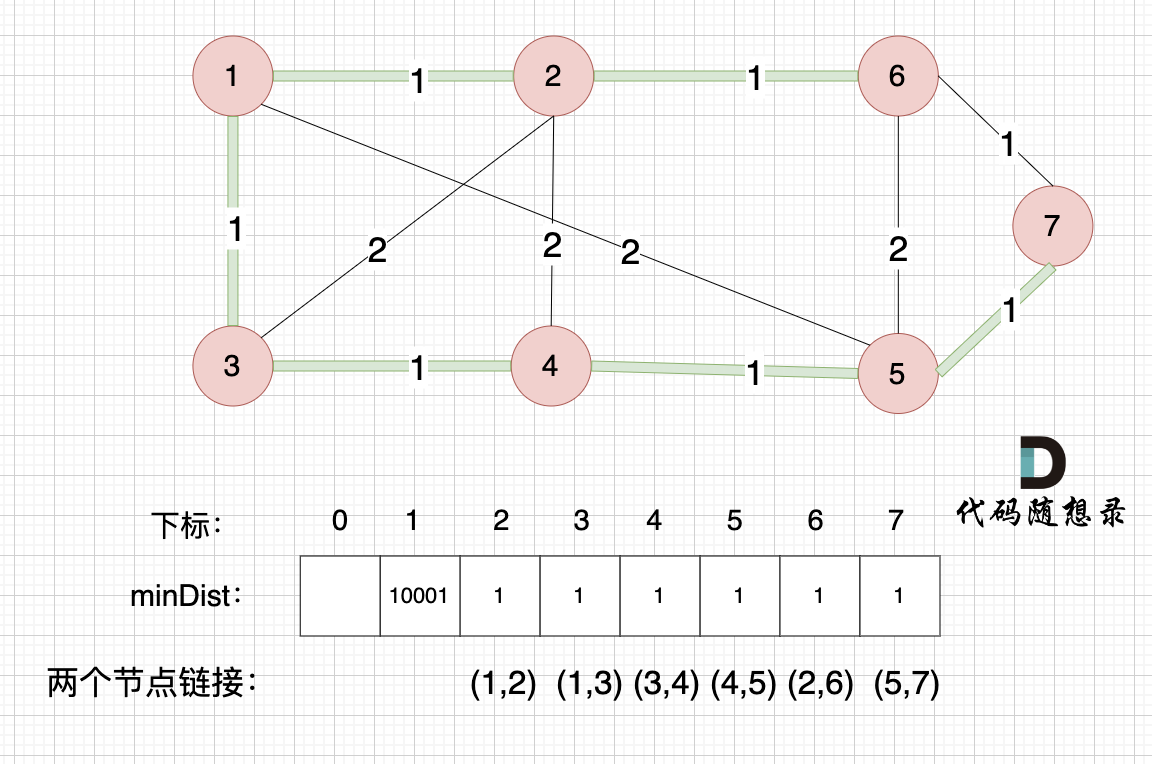
最后

最后我们就生成了一个最小生成树，绿色的边将所有节点链接到一起，并且保证权值是最小的，因为我们在更新 minDist 数组的时候，都是选距离最小生成树最近的点加入到树中。

讲解上面的模拟过程的时候，我已经强调多次 minDist数组是记录了所有非生成树节点距离生成树的最小距离。

最后，minDist数组也就是记录的是最小生成树所有边的权值。

我在图中，特别把每条边的权值对应的是哪两个节点标记出来（例如minDist[7] = 1，对应的是节点5 和节点7之间的边，而不是节点6 和节点7），为了就是让大家清楚， minDist里的每一个值对应的是哪条边。

那么我们要求最小生成树里边的权值总和就是把最后的 minDist 数组累加一起。

以下代码，我对 prim三部曲，做了重点注释，大家根据这三步，就可以透彻理解prim。

#include<iostream>
#include<vector>
#include <climits>

using namespace std;
int main() {
    int v, e;
    int x, y, k;
    cin >> v >> e;
    // 填一个默认最大值，题目描述val最大为10000
    vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001));
    while (e--) {
        cin >> x >> y >> k;
        // 因为是双向图，所以两个方向都要填上
        grid[x][y] = k;
        grid[y][x] = k;

    }
    // 所有节点到最小生成树的最小距离
    vector<int> minDist(v + 1, 10001);

    // 这个节点是否在树里
    vector<bool> isInTree(v + 1, false);

    // 我们只需要循环 n-1次，建立 n - 1条边，就可以把n个节点的图连在一起
    for (int i = 1; i < v; i++) {

        // 1、prim三部曲，第一步：选距离生成树最近节点
        int cur = -1; // 选中哪个节点 加入最小生成树
        int minVal = INT_MAX;
        for (int j = 1; j <= v; j++) { // 1 - v，顶点编号，这里下标从1开始
            //  选取最小生成树节点的条件：
            //  （1）不在最小生成树里
            //  （2）距离最小生成树最近的节点
            if (!isInTree[j] &&  minDist[j] < minVal) {
                minVal = minDist[j];
                cur = j;
            }
        }
        // 2、prim三部曲，第二步：最近节点（cur）加入生成树
        isInTree[cur] = true;

        // 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
        // cur节点加入之后， 最小生成树加入了新的节点，那么所有节点到 最小生成树的距离（即minDist数组）需要更新一下
        // 由于cur节点是新加入到最小生成树，那么只需要关心与 cur 相连的 非生成树节点 的距离 是否比 原来 非生成树节点到生成树节点的距离更小了呢
        for (int j = 1; j <= v; j++) {
            // 更新的条件：
            // （1）节点是 非生成树里的节点
            // （2）与cur相连的某节点的权值 比 该某节点距离最小生成树的距离小
            // 很多录友看到自己 就想不明白什么意思，其实就是 cur 是新加入 最小生成树的节点，那么 所有非生成树的节点距离生成树节点的最近距离 由于 cur的新加入，需要更新一下数据了
            if (!isInTree[j] && grid[cur][j] < minDist[j]) {
                minDist[j] = grid[cur][j];
            }
        }
    }
    // 统计结果
    int result = 0;
    for (int i = 2; i <= v; i++) { // 不计第一个顶点，因为统计的是边的权值，v个节点有 v-1条边
        result += minDist[i];
    }
    cout << result << endl;

}

时间复杂度为 O(n^2)，其中 n 为节点数量。

kruskal算法精讲

1、题目

题目描述：

在世界的某个区域，有一些分散的神秘岛屿，每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路，方便运输。

不同岛屿之间，路途距离不同，国王希望你可以规划建公路的方案，如何可以以最短的总公路距离将所有岛屿联通起来。

给定一张地图，其中包括了所有的岛屿，以及它们之间的距离。以最小化公路建设长度，确保可以链接到所有岛屿。

输入描述：

第一行包含两个整数V 和 E，V代表顶点数，E代表边数。顶点编号是从1到V。例如：V=2，一个有两个顶点，分别是1和2。

接下来共有 E 行，每行三个整数 v1，v2 和 val，v1 和 v2 为边的起点和终点，val代表边的权值。

输出描述：

输出联通所有岛屿的最小路径总距离

输入示例：

输出示例：

2、题解

在上一篇我们讲解了 prim算法求解最小生成树，本篇我们来讲解另一个算法：Kruskal，同样可以求最小生成树。

prim 算法是维护节点的集合，而 Kruskal 是维护边的集合。

上来就这么说，大家应该看不太懂，这里是先让大家有这么个印象，带着这个印象在看下文，理解的会更到位一些。

kruscal的思路：

边的权值排序，因为要优先选最小的边加入到生成树里
遍历排序后的边
- 如果边首尾的两个节点在同一个集合，说明如果连上这条边图中会出现环
- 如果边首尾的两个节点不在同一个集合，加入到最小生成树，并把两个节点加入同一个集合

下面我们画图举例说明kruscal的工作过程。

依然以示例中，如下这个图来举例。

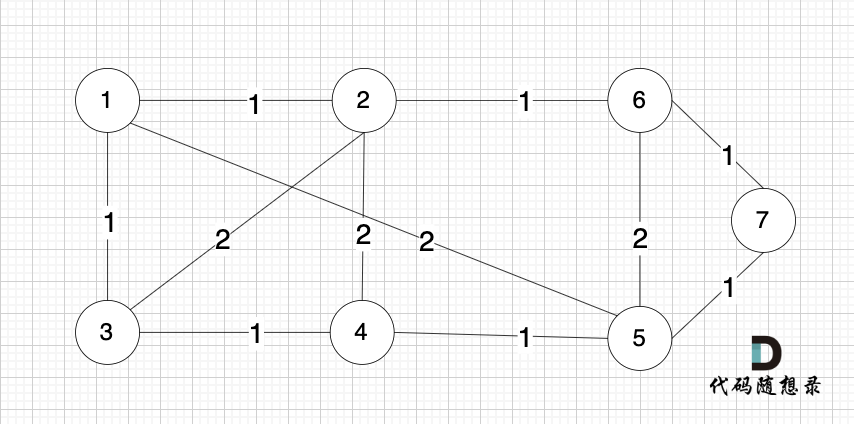
将图中的边按照权值有小到大排序，这样从贪心的角度来说，优先选权值小的边加入到最小生成树中。

排序后的边顺序为[(1,2) (4,5) (1,3) (2,6) (3,4) (6,7) (5,7) (1,5) (3,2) (2,4) (5,6)]

(1,2) 表示节点1 与节点2 之间的边。权值相同的边，先后顺序无所谓。

开始从头遍历排序后的边。

选边(1,2)，节点1 和节点2 不在同一个集合，所以生成树可以添加边(1,2)，并将节点1，节点2 放在同一个集合。

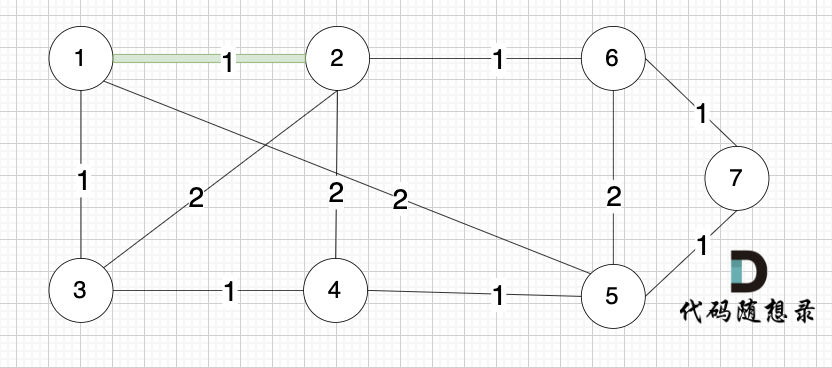
选边(4,5)，节点4 和节点 5 不在同一个集合，生成树可以添加边(4,5) ，并将节点4，节点5 放到同一个集合。

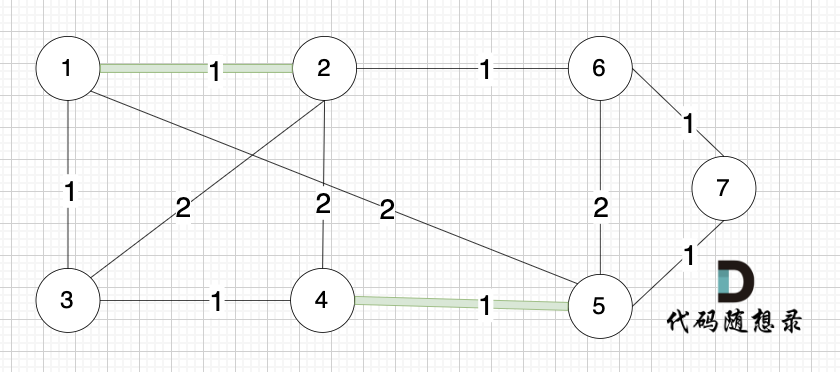
大家判断两个节点是否在同一个集合，就看图中两个节点是否有绿色的粗线连着就行

（这里在强调一下，以下选边是按照上面排序好的边的数组来选择的）

选边(1,3)，节点1 和节点3 不在同一个集合，生成树添加边(1,3)，并将节点1，节点3 放到同一个集合。

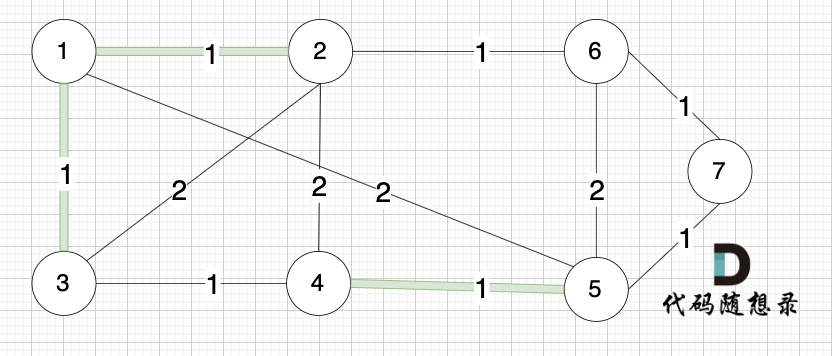
选边(2,6)，节点2 和节点6 不在同一个集合，生成树添加边(2,6)，并将节点2，节点6 放到同一个集合。

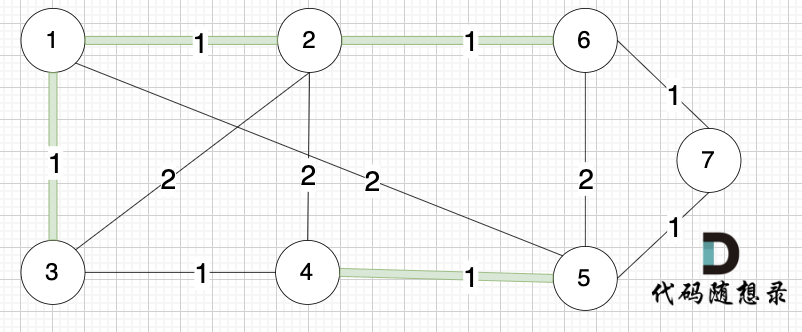
选边(3,4)，节点3 和节点4 不在同一个集合，生成树添加边(3,4)，并将节点3，节点4 放到同一个集合。

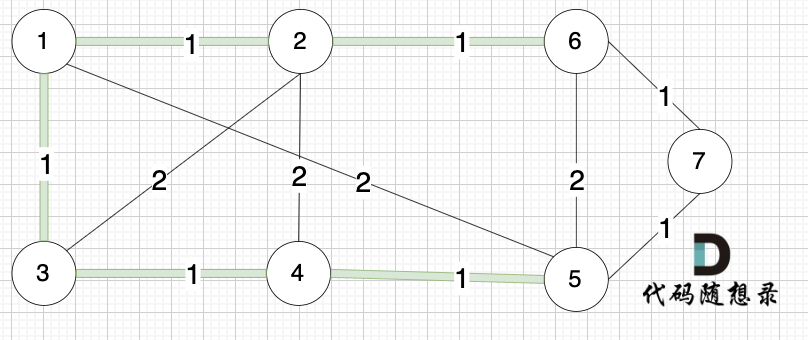
选边(6,7)，节点6 和节点7 不在同一个集合，生成树添加边(6,7)，并将节点6，节点7 放到同一个集合。

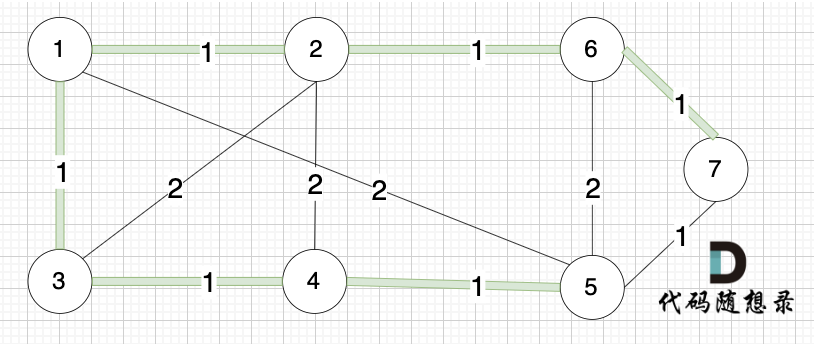
选边(5,7)，节点5 和节点7 在同一个集合，不做计算。

选边(1,5)，两个节点在同一个集合，不做计算。

后面遍历边(3,2)，(2,4)，(5,6) 同理，都因两个节点已经在同一集合，不做计算。

此时我们就已经生成了一个最小生成树，即：

在上面的讲解中，看图的话大家知道如何判断两个节点是否在同一个集合（是否有绿色的线连在一起），以及如何把两个节点加入集合（就在图中把两个节点连上）

但在代码中，如果将两个节点加入同一个集合，又如何判断两个节点是否在同一个集合呢？

这里就涉及到我们之前讲解的并查集。

我们在并查集开篇的时候就讲了，并查集主要就两个功能：

将两个元素添加到一个集合中
判断两个元素在不在同一个集合

大家发现这正好符合 Kruskal算法的需求，这也是为什么 要先讲并查集，再讲 Kruskal。

本题代码如下，已经详细注释：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// l,r为 边两边的节点，val为边的数值
struct Edge {
    int l, r, val;
};

// 节点数量
int n = 10001;
// 并查集标记节点关系的数组
vector<int> father(n, -1); // 节点编号是从1开始的，n要大一些

// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}

// 并查集的查找操作
int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}

// 并查集的加入集合
void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

int main() {

    int v, e;
    int v1, v2, val;
    vector<Edge> edges;
    int result_val = 0;
    cin >> v >> e;
    while (e--) {
        cin >> v1 >> v2 >> val;
        edges.push_back({v1, v2, val});
    }

    // 执行Kruskal算法
    // 按边的权值对边进行从小到大排序
    sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) {
            return a.val < b.val;
    });

    // 并查集初始化
    init();

    // 从头开始遍历边
    for (Edge edge : edges) {
        // 并查集，搜出两个节点的祖先
        int x = find(edge.l);
        int y = find(edge.r);

        // 如果祖先不同，则不在同一个集合
        if (x != y) {
            result_val += edge.val; // 这条边可以作为生成树的边
            join(x, y); // 两个节点加入到同一个集合
        }
    }
    cout << result_val << endl;
    return 0;
}