
聚类算法
聚类是一种经典的无监督学习方法,无监督学习的目标是通过对无标记训练样本的学习,发掘和揭示数据集本身潜在的结构与规律,即不依赖于训练数据集的类标记信息。聚类则是试图将数据集的样本划分为若干个互不相交的类簇,从而每个簇对应一个潜在的类别。
聚类算法全面解析
1.距离度量基础
1.1 闵可夫斯基距离族
通用公式:
d
i
s
t
m
k
(
x
i
,
x
j
)
=
(
∑
u
=
1
n
x
i
u
−
x
j
u
p
)
1
/
p
dist_{mk}(x_i,x_j) = (\sum_{u=1}^n x_{iu}-x_{ju} ^p)^{1/p}
distmk(xi,xj)=(u=1∑nxiu−xjup)1/p
常见变体:
-
曼哈顿距离(p=1): d i s t = ∑ x i − y i dist = ∑x_i - y_i dist=∑xi−yi
-
欧氏距离(p=2): d i s t = √ ( ∑ ( x i − y i ) 2 ) dist = √(∑(x_i - y_i)²) dist=√(∑(xi−yi)2)
1.2 属性类型处理
由于属性分为连续属性与离散属性。连续属性可以直接使用距离公式计算,对于离散属性而言还要再分为有序属性和无序属性,有序属性可以连续化然后通过距离公式计算,而无需属性则需要使用one-hot编码再使用VDM距离法。
- 有序属性 直接参与计算 身高:高(1)→中(0.5)→矮(0)
- 无序属性 VDM距离法 性别:(男→[1,0], 女→[0,1])
VDM距离公式:

聚类性能评估
2.1 外部指标
由于无监督,因此不能对比标签来看聚类模型得准确率。因此此时找到一个外部得参考模型得输出作为伪标签,然后评价聚类效果

2.2 内部指标
基于聚类结果自身特性进行评估

原型聚类算法
3.1 K-Means
K-Means的思想十分简单,首先随机指定类中心,根据样本与类中心的远近划分类簇,接着重新计算类中心,迭代直至收敛。但是其中迭代的过程并不是主观地想象得出,事实上,若将样本的类别看做为“隐变量”(latent variable),类中心看作样本的分布参数,这一过程正是通过 EM算法的两步走 策略而计算出,其根本的目的是为了最小化平方误差函数E:
E
=
∑
i
=
1
k
∑
x
∈
C
i
∣
x
−
μ
i
∣
2
E=\sum_{i=1}^k \sum_{x\in C_i} |x-\mu_i|^2
E=i=1∑kx∈Ci∑∣x−μi∣2

Kmeans++算法:更优的初始化
1.随机选择第一个中心点作为第一个类别
2.计算每个点到已有中心的最短距离D(x)(如果有多个中心的话就选择最短距离作为D(x))
3.按概率 P = D ( x ) 2 / ∑ D ( x ) 2 P= D(x)^2/ \sum D(x)^2 P=D(x)2/∑D(x)2选择下一个中心作为下一个类别标记
4.直到选满K个类别
选择下一个中心
3.2 学习向量量化(LVQ)
首先面对标注真实标签的数据,是一个半监督算法。从每个类别中挑选出一个作为圆形特征向量。然后再从样本集中随机挑选样本 x i x_i xi来计算 x i x_i xi与每个原型特征的距离,选择最近的距离作为 x i x_i xi的预测标签。如果分类正确,则原型向量靠近样本向量,如果分类不正确则远离。
通过**"奖励-惩罚"机制更新原型向量**
更新规则:
{
p
′
=
p
+
η
(
x
−
p
)
分类正确
p
′
=
p
−
η
(
x
−
p
)
分类错误
\begin{cases} p' = p + \eta(x-p) & \text{分类正确} \\ p' = p - \eta(x-p) & \text{分类错误} \end{cases}
{p′=p+η(x−p)p′=p−η(x−p)分类正确分类错误

3.3 高斯混合聚类

概率模型:
p
(
x
)
=
∑
i
=
1
k
α
i
⋅
N
(
x
∣
μ
i
,
Σ
i
)
p(x) = \sum_{i=1}^k \alpha_i \cdot N(x|\mu_i,\Sigma_i)
p(x)=i=1∑kαi⋅N(x∣μi,Σi)
EM算法步骤:
-
E步:计算后验概率γ
-
M步:更新参数:
μ
i
=
∑
γ
j
i
x
j
∑
γ
j
i
\mu_i = \frac{\sum γ_{ji}x_j}{\sum γ_{ji}}
μi=∑γji∑γjixj

🌟 DBSCAN算法完全解析:从背景到实践
🔍 算法提出的背景
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) 诞生于解决传统聚类算法三大局限:
- 形状限制:K-Means等算法只能识别凸形簇,无法处理复杂形状
- 噪声敏感:传统算法对噪声点缺乏鲁棒性
- 密度差异:无法自动适应不同区域的数据密度
举个例子🌰:假设地图上有这些位置:
- 密集居民区(高密度点集)
- 零散便利店(中等密度点集)
- 郊区独立屋(低密度点集)
- 偏远加油站(孤立噪声点)
传统聚类会将郊区住宅误认为噪声,而DBSCAN能精准识别所有区域!
📊 算法操作的数据特点
DBSCAN处理的数据需满足:
- 可测距性:能计算任意两点间距离
- 欧氏距离: d i s t = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 dist = \sqrt{ (x₁-x₂)² + (y₁-y₂)² } dist=(x1−x2)2+(y1−y2)2
- 余弦相似度:适合文本数据
- 特征向量表示:每个数据点为向量形式
- 房价数据:
[面积, 房间数, 经度, 纬度] - 用户画像:
[活跃度, 消费金额, 年龄]
- 房价数据:
- 维度无限制:适合高维空间(但需要调整参数)
# 典型数据集格式
import numpy as np
data = np.array([
[35.2, -118.3], # 洛杉矶
[40.7, -74.0], # 纽约
[51.5, -0.1], # 伦敦
[48.9, 2.3], # 巴黎郊区
[48.8, 2.4] # 巴黎郊区
])
关键概念
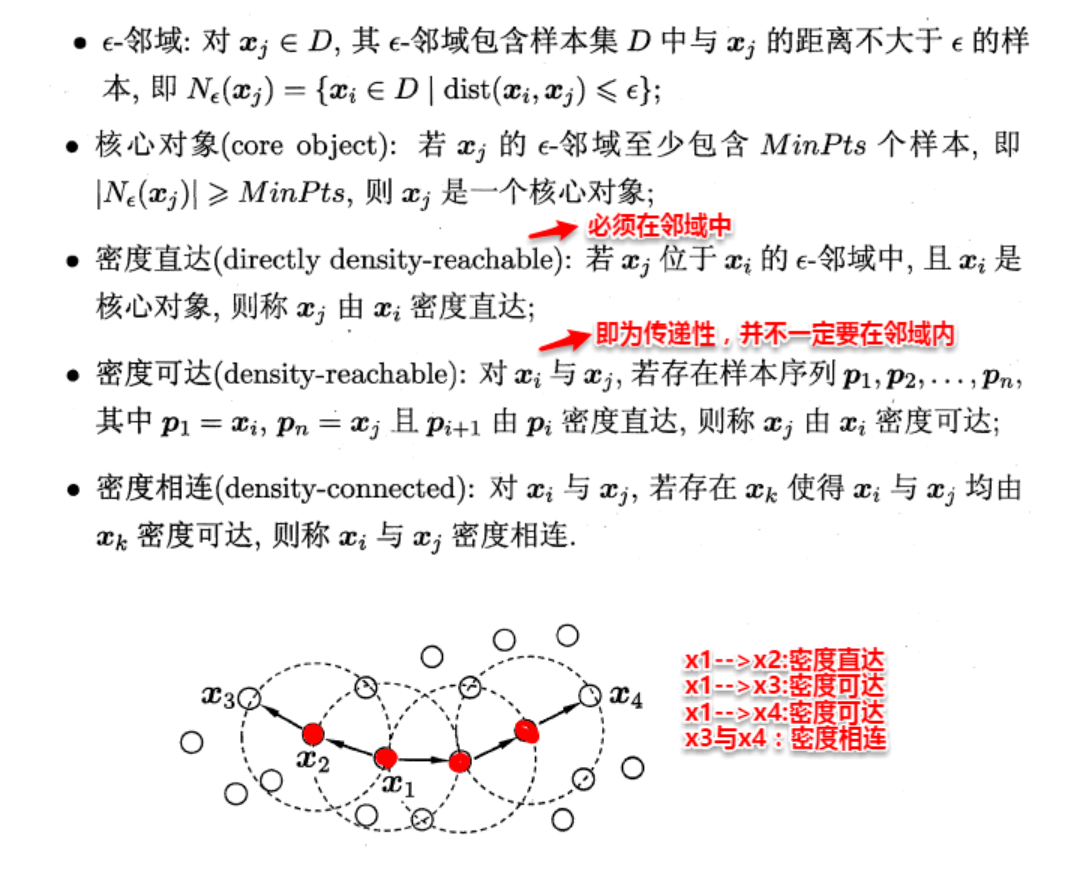
🔧 算法流程详解
DBSCAN通过两个核心参数工作:
-
ε (eps):邻域半径
-
MinPts:核心点阈值
算法分为两个步骤:1.标记所有核心对象(满足len<MinPts)2.将所有密度可直达的点划分为一个cluster


层次聚类(AGNES)
非常像哈夫曼树呢怎么??
🧠 AGNES算法提出的背景
层次聚类诞生的核心动机是解决"数据层次关系可视化"问题。不同于K-Means等划分式聚类,AGNES (AGglomerative NESting) 的独特价值在于:
- 生物分类学启发
受生物分类系统(界-门-纲-目…)启发,适用于需要多层级分析的场景:
- 基因家族进化树
- 文档主题分层体系
- 企业组织架构
-
应对现实数据的层次性
当数据存在自然嵌套结构时(如:动物 → 哺乳类 → 猫科 → 家猫),
扁平聚类会丢失层次化的嵌套结构关系 -
无需预设簇数
传统方法需提前指定k值(如K-Means),而AGNES通过树状图(Dendrogram) 展示所有可能划分
简言之:AGNES像"数据显微镜",能观察样本在不同粒度下的聚类关系
🔧 算法流程详解(结合您提供的伪代码)
AGNES采用自底向上策略,流程分为三阶段:
阶段1:初始化(对应伪代码1-9行)
每个样本单独归为一个簇。n个样本n个簇,并且构建n×n的对称距离矩阵
距离的计算采用三种链接之一

阶段2:迭代合并(对应伪代码10-23行)
取出距离矩阵中最小的两个簇合并。去掉这两个簇,并且将合并的新簇添加进入队列,并且更新距离矩阵。

很容易看出:单链接的包容性极强,稍微有点暧昧就当做是自己人了,全链接则是坚持到底,只要存在缺点就坚决不合并,均连接则是从全局出发顾全大局。
头歌实战
距离计算
#encoding=utf8
import numpy as np
def distance(x,y,p=2):
'''
input:x(ndarray):第一个样本的坐标
y(ndarray):第二个样本的坐标
p(int):等于1时为曼哈顿距离,等于2时为欧氏距离
output:distance(float):x到y的距离
'''
#********* Begin *********#
#一定注意x,y都是多维空间的
if p == 1:
return np.sum(np.abs(x-y))
else:
return np.sum(np.abs(x-y)**p)**(1.0/p)
#********* End *********#
计算质心距离并且排序
看清楚怎么使用sort()的
#encoding=utf8
import numpy as np
# 计算样本间距离
def distance(x, y, p=2):
'''
input:x(ndarray):第一个样本的坐标
y(ndarray):第二个样本的坐标
p(int):等于1时为曼哈顿距离,等于2时为欧氏距离
output:distance(float):x到y的距离
'''
#********* Begin *********#
# 计算x和y之间差的绝对值的p次方
dis = np.sum(np.abs(x - y) ** p) ** (1.0 / p)
# 计算最终的距离值
#********* End *********#
return dis
# 计算质心
def cal_Cmass(data):
'''
input:data(ndarray):数据样本
output:mass(ndarray):数据样本质心
'''
#********* Begin *********#
# 计算数据样本的质心(每个维度的平均值)
# 使用axis=0确保正确处理多维数组
Cmass = np.mean(data, axis=0)
#********* End *********#
return Cmass
# 计算每个样本到质心的距离,并按照从小到大的顺序排列
def sorted_list(data, Cmass):
'''
input:data(ndarray):数据样本
Cmass(ndarray):数据样本质心
output:dis_list(list):排好序的样本到质心距离
'''
#********* Begin *********#
# 初始化一个空列表,用于存储距离
dist_list = []
# 遍历数据样本中的每个样本
for x in data:
dist_list.append(distance(x, Cmass))
# 对距离列表进行排序
dist_list.sort()
# 转换为NumPy数组
#********* End *********#
return dist_list
K-means
K-means:
两个关键变量
- 样本集X(sample_num,featrues)
- clusters,K行,每行若干个索引——代表X样本的分类结果
- centroids(K,featrues),K个类别中心
#encoding=utf8
import numpy as np
# 计算一个样本与数据集中所有样本的欧氏距离的平方
def euclidean_distance(one_sample, X):
one_sample = one_sample.reshape(1, -1)
distances = np.power(np.tile(one_sample, (X.shape[0], 1)) - X, 2).sum(axis=1)
return distances
class Kmeans():
"""Kmeans聚类算法.
Parameters:
-----------
k: int
聚类的数目.
max_iterations: int
最大迭代次数.
varepsilon: float
判断是否收敛, 如果上一次的所有k个聚类中心与本次的所有k个聚类中心的差都小于varepsilon,
则说明算法已经收敛
"""
def __init__(self, k=2, max_iterations=500, varepsilon=0.0001):
self.k = k
self.max_iterations = max_iterations
self.varepsilon = varepsilon
np.random.seed(1)
#********* Begin *********#
#clusters,K行,每行若干个索引
#centroids(K,featrues),K个类别中心
# 从所有样本中随机选取self.k样本作为初始的聚类中心
def init_random_centroids(self, X):
#生成从0到样本数量的k个随机不重复索引np.random.choice,replace=Falsed代表无放回
random_indices = np.random.choice(X.shape[0],self.k,replace=False)
#选择出的索引可能为[1,3,24,54]
return X[random_indices]
# 返回距离该样本最近的一个中心索引[0, self.k)
def _closest_centroid(self, sample, centroids):
#广播机制的应用
# distance = np.sum((sample-centroids)**2)**(1.0/2)错误,直接使用np.sum会将所有维度的差值平方嘉禾成一个标量值。
#应该是用np.sum(,axis=1)得到一个形状为 (k,) 的距离向量
distance = np.sum((sample-centroids)**2,axis=1)**(1.0/2)
#返回该样本属于哪个中心的中心索引
return np.argmin(distance)
# 将所有样本进行归类,归类规则就是将该样本归类到与其最近的中心
def create_clusters(self, centroids, X):
clusters = [[] for _ in range(self.k)]#二维数组,k行代表一共k个簇,每行存储对应的样本
#遍历所有样本
for i, sample in enumerate(X):
centroid_index=self._closest_centroid(sample,centroids)
clusters[centroid_index].append(i)
return clusters
#cluster为[k],每行保存X的对应索引
# 对中心进行更新
def update_centroids(self, clusters, X):
#初始化新的聚类中心数组(K,featrues),老的已经分完类的二维数组clusters存储了每个类的数组,cluster 中包含有若干个索引
centroids = np.zeros((self.k,X.shape[1]))
#遍历每个簇
for i,cluster in enumerate(clusters):
if cluster:
centroids[i]=np.mean(X[cluster],axis=0)#得到(,features)
else:#簇为空
centroids[i]=X[np.random.choice(X.shape[0],1,replace=False)].flatten()#X[random]需要展平得到一维向量
return centroids
# 将所有样本进行归类,其所在的类别的索引就是其类别标签
def get_cluster_labels(self, clusters, X):
#初始化标签数组,大小为样本数
labels=np.empty(X.shape[0])
#为每个簇的样本分配标签
for i,cluster in enumerate(clusters):
for sample_index in cluster:
labels[sample_index]=i
return labels
# 对整个数据集X进行Kmeans聚类,返回其聚类的标签
def predict(self, X):
# 从所有样本中随机选取self.k样本作为初始的聚类中心
centroids= self.init_random_centroids(X)
# 迭代,直到算法收敛(上一次的聚类中心和这一次的聚类中心几乎重合)或者达到最大迭代次数
for _ in range(self.max_iterations):
#保存上一代的中心
pre_cen = centroids.copy()
# 将所有X进行归类,归类规则就是将该样本归类到与其最近的中心
clusters = self.create_clusters(centroids,X)
# 计算新的聚类中心
centroids = self.update_centroids(clusters,X)
# 如果聚类中心几乎没有变化,说明算法已经收敛,退出迭代
distances=np.sum((pre_cen-centroids)**2,axis=1)**(1.0/2)
if np.all(distances<self.varepsilon):
break;
labels = self.get_cluster_labels(clusters,X)
return labels
#********* End *********#
sklearn实战K-means
#encoding=utf8
from sklearn.cluster import KMeans
def kmeans_cluster(data):
'''
input:data(ndarray):样本数据
output:result(ndarray):聚类结果
'''
#********* Begin *********#
Kmeans=KMeans(n_clusters=3,random_state=10)
Kmeans.fit(data)
result=Kmeans.labels_
#********* End *********#
return result
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








